Сосуществование фаз в однокомпонентной системе.

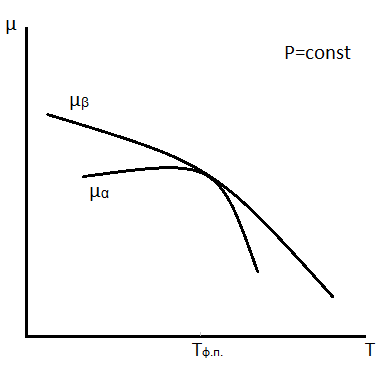
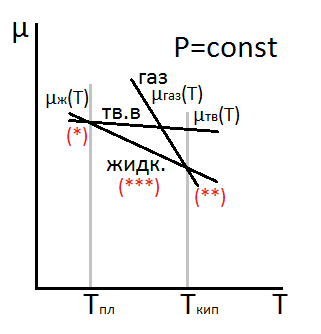Чтобы понять как происходит переход твёрдой фазы в жидкую, а затем в газообразную при нагревании при постоянном давлении, рассмотрим поведение 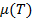при P=const для различных фаз (см. рис.)

Как уже указывалось, устойчивой является фаза с самым низким химическим потенциалом.

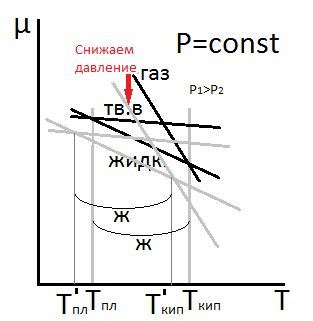
Если 2 или большее число фаз имеют одинаковый µ, то они сосуществуют в положении равновесия: это, например, Т_кип и Т_пл. Ниже Т_пл самый низкий потенциал µ у твёрдой фазы и поэтому она устойчива (*). Выше точки кипения самый низкий µ у газовой фазы (**), устойчивой в этих условиях. Между Т_кип и Т_пл устойчивой является жидкая фаза (***). Из рисунка видно, что фазовые превращения происходят не постепенно, а сразу и пока Т не достигла точки перехода, ни что на графике не указывает на существенные изменения в системе.

Наклон линий выражается:

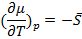
(3.4)

S вещества больше нуля, поэтому наклон отрицателен. Поскольку 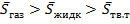, следовательно графики должны иметь именно тот вид, как показан на рисунке.

При более низком давлении линии, выражающие зависимости µ(Т) оказываются смещёнными.

Влияние давления на химический потенциал чистого вещества при Т = const выражается

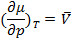
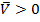всегда, значит µ уменьшается всегда при уменьшении P при постоянной температуре.

Известно что 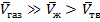=> этот эффект снижения µ для газа значительно больше, чем для жидкости или твёрдого тела.

Можно ожидать, что уменьшение давления понизит точку кипения значительно больше, чем понизит точку плавления, т.к. 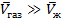, а .

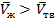В результате снижается диапазон температур, в котором жидкость является устойчивой фазой.

Очевидно, что при достаточно низком давлении кривая µ для газа пересечёт кривую µ для твёрдого тела ниже той температуры, где µ_тв.т = µ_ж и µ_тв.т= µ_газ.

Это означает, что при такой температуре твёрдое тело не плавиться а возгоняться (пример - сухой лёд).

В пределе при определении p кривая µ для твёрдого тела , жидкости и пара пересекутся в одной точке. Сочетание T и P, при котором сосуществуют 3 фазы, называется тройной точкой.

3.6 Фазовые переходы в однокомпонентной системе.

Согласно критериям равновесия выраженным через интенсивные величины 3.2при равновесии химические потенциалы компонента во всех фазах одинаковы, т.е. для однокомпонентной системы µ_α= µ_β. Пусть α, β - равновесные фазы, это соответствует набору µ(Т) кривых при любом постоянном давлении.

Или

µ_α(Т,P)= µ_β(T,P)

Это есть уравнение для функциональной зависимости P=f(T).

Состояние однокомпонентной системы изображается в координатах в виде фазовой диаграммы. Приходим к фазовой диаграмме. Решение уравнений даёт точки на кривых 1, 2, 3 рисунка. Это линии равновесия, вдоль которых сосуществуют 2 фазы.

1 - кривая сублимации (возгонки) равновесие твёрдой и газообразной фаз.

2 - кривая испарения, (оканчивается в критической точке) равновесие жидкой и газовой фаз (насыщенный пар).

3 - кривая плавления (равновесие твёрдоё и жидкой фаз).

Каждая кривая равновесия разделяет две смежные однофазные области, в которых система бивариантна. Изменение её состояния, происходящее вдоль линии, которая пересекает кривую равновесия, соответствует фазовому превращению - это фазовый переход первого рода.

Покажем, что фазовые переходы первого рода соответствуют превращениям вещества типа жидкость-газ, твердое тело - жидкость и т.д., всегда сопровождаются тепловым эффектом с изменением мольного объёма.

Пусть P=const.

Изобразим температурную зависимость химических потенциалов одного и того же вещества, находящегося в двух фазах α и β при постоянном давлении.

Учтём реальныё ход зависимости µ(Т) и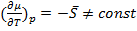

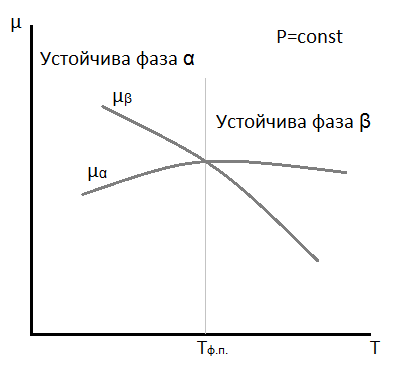Точка пересечения µ потенциалов даёт Т фазового перехода, при которой в соответствии с µ_α(Т,P)= µ_β(T,P) две фазы α и β находятся при P=const.

Если изменяется P, то температура Т_ф.п. изменяется по кривым 1, 2, 3 диаграммы P-T.

При Т≠ Т_ф.п., устойчивой является та фаза, которая имеет наименьший химический потенциал.

В однокомпонентной системе n=const, что обеспечивает минимальность свободной энергии Гиббса G=µ*n.

Фаза α существует при Т< Т_ф.п. - низкотемпературная фаза.

Фаза β существует при Т> Т_ф.п. - высокотемпературная фаза.

Результирующий ход µ описывается нижними частями кривых µ(T).

В точке фазового перехода имеется излом хода µ(T).

Причём

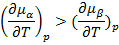
или

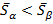
Рассмотрим увеличение температуры:

Фазовый переход 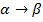, который возникает при увеличении температуры и сопротивляется изменениям мольной энтропии скачком на величину .

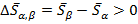Так как переход происходит равновесным образом, то есть s w:val="24"/><w:lang w:fareast="RU"/></w:rPr><m:t>S</m:t></m:r></m:e></m:acc></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> =>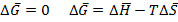

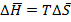
И изменение энтальпии

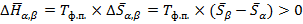
(3.5)

То есть появляется в виде поглощаемой теплоты называется скрытая теплота фазового перехода.

Термин означает, что поглощение тепла не приводит к изменению температуры системы. Куда оно расходуется? Оно расходуется на перестройку структуры вещества при Т_ф.п.=const.

Очевидно, что при уменьшении температуры:

для обратного перехода 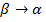при понижении температуры мы имеем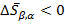 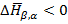теплота выделяется.

Таким образом имеем скачок энтальпии и энтропии при Т_{плавлении-кристализации}(аналогично Т_кип).

Пусть теперь зафиксируем µ(P) при этом 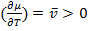, наклон >0. Тогда в (.) фазового перехода Т_ф.п. µ_α(P)= µ_β(P),

при этом:

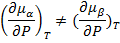
или

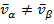
Таким образом, фазовый переход 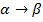всегда сопровождается изменением мольного объёма на величину

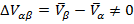
(3.5')

Для процессов испарения и сублимации, конечное состояние вещества газообразное, тогда

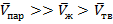
Значит всегда .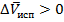

Определение

Фазовый переход первого рода характеризуется скачком первой производной µ по T и P.

Наряду с этим в природе наблюдаются физические ситуации, когда в точке фазового перехода µ пересекаются с одновременным касанием. Это означает (обеспечивает) непрерывность первых производных. при этом вторые частные производные могут меняться скачком. Это фазовый переход второго рода.

В силу отсутствия скачка первых производных

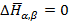
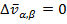
(3.6)

При этом физические величины, выражающиеся через вторые частные производные претерпевают резкие изменения:

Изобарный коэффициент теплового расширения

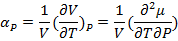
(3.7)

изотермическая сжимаемость

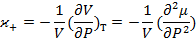
(3.7)'

изобарная теплоёмкость

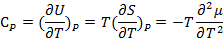
(3.7)''

Фазовые переходы второго рода наблюдаются, как правило, в твёрдой фазе и связанны с изменением симметрии твёрдого тела:

ферромагнетик - парамагнетик

сегнетоэлектрик - параэлектрик.

3.7 Уравнение Клапейрона

(применяем к фазовым переходам первого рода)

µ_α= µ_β

Когда две фазы чистого вещества находятся в равновесии их µ одинаковы при данных T и P const.

Пусть P=const, T меняется или при T=const, P меняется, то одна из фаз исчезнет (например, жидкая фаза при уменьшении P).

Пусть P, T изменяются так, что µ_α= µ_β, тогда существуют обе фазы.

Клапейрон вывел уравнение для .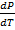

Пусть α, β - фазы, находящиеся в равновесии =>

µ_α= µ_β или 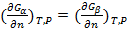(парциальные мольные пробарные потенциалы)

(3.7)

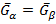
Если P,T изменяются так, что равновесие сохраняется => скорости изменения

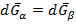
Так как G(P,T) полный дифференциал, перепишем:

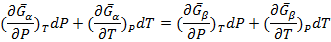
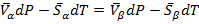
или

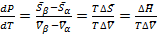- ур-е Клапейрона

(3.8)

Это уравнение можно применять к испарению, возгонке, плавлению или взаимному превращению 2 твёрдых фаз чистого вещества (полиморфизм).

При данной температуре существует соотношение:

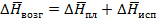
т.к. количество теплоты, необходимое для испарения данного количества твёрдого вещества есть const независимо от того как проводится процесс непосредственно или нет.

[H]=[PΔV]

Уравнение Клазиуса - Клапейрона

Клазиус упростил уравнение Клайперона применив его к испарению и возгонке, предложив

1) пар - идеальный газ.

2) .

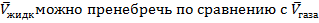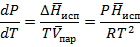
(3.9)

Этим уравнением удобно пользоваться, если изменения T и P малы.

Можно внести поправку в T_кип при колебаниях P_атм.

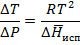
Преобразуем уравнение (3.9), поделив на Р:

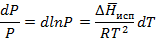
Пусть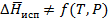

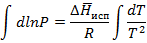
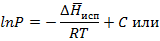
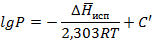
Таким образом, зависимость lgP(1/T) линейная, что подтверждается экспериментально для испарения и возгонки водяного пара.

В широком диапазоне Т наблюдаются отклонения.

1) результаты расчёта не более точны, чем предположение об идеальном газе и используемого уравнения .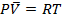

2)

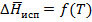
По этому уравнению можно расчитать теплоту испарения или возгонки.

Мольная энтропия испарения в стационарной точке (Т_кип при 1 атм) для многих жидкостей постоянна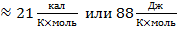

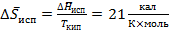- уравнение Трутона

(3.10)

Оно полезно для оценки мольной теплоты испарения жидкости с известной температурой кипения.