Дифференцирование по параметру собственного интеграла с постоянными пределами интегрирования
Теорема 2.10 Пусть функция f(x, у) непрерывна на П, а функции а(у), b(у) непрерывны на [с; d]. Тогда функция I(у), определённая равенством (2.6),непрерывна на [с; d].
Доказательство. Пусть y 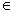 [с; d]. Покажем, что
[с; d]. Покажем, что 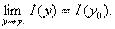 Для этого разобьём интеграл на три слагаемых, используя свойство аддитивности интеграла.
Для этого разобьём интеграл на три слагаемых, используя свойство аддитивности интеграла.
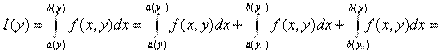
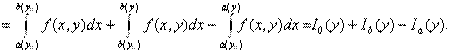 (2.7)
(2.7)
Здесь интегралы обозначены в порядке следования. Рассмотрим каждый из них в отдельности. Первый из интегралов — интеграл с постоянными пределами вида 2.1, его непрерывность доказана в теореме 2.7. Поэтому 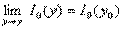
Займемся вторым интегралом. Функция f(x, у) непрерывна на П, следовательно, ограничена. Поэтому существует постоянная М такая, что
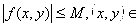 П.
П.
Но тогда
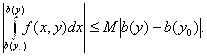
А так как функция b(у) непрерывна на [с; d], то 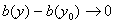 при
при 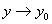 , поэтому
, поэтому 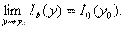
Совершенно аналогично доказывается, что и 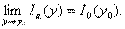
Таким образом,

что и требовалось доказать.
Собственные интегралы, зависящие от параметра для прямоугольника и их свойства
Теорема 4 (о непрерывности интеграла как функции параметра). Пусть функция 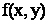 определена и непрерывна в прямоугольнике
определена и непрерывна в прямоугольнике 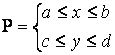 , тогда интеграл
, тогда интеграл 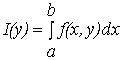 будет непрерывной функцией от параметра
будет непрерывной функцией от параметра 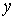 в промежутке
в промежутке 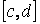 .
.
Доказательство.
Так как 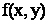 непрерывна на замкнутом множестве, то по теореме Кантора она равномерно непрерывна на данном прямоугольнике
непрерывна на замкнутом множестве, то по теореме Кантора она равномерно непрерывна на данном прямоугольнике 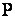 . Возьмем любое
. Возьмем любое 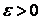 и зафиксируем
и зафиксируем 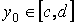 . Тогда нашему значению
. Тогда нашему значению 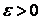 будет соответствовать
будет соответствовать 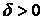 , такое, что для любых двух точек
, такое, что для любых двух точек 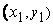 ,
, 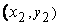 принадлежащих
принадлежащих 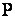 , из неравенств
, из неравенств 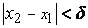 и
и 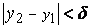 , будет следовать
, будет следовать 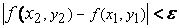 . Положим
. Положим 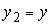 ,
, 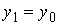 , где
, где 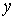 ,
, 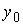 - любые из
- любые из 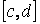 , и
, и 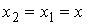 , где
, где  . Тогда получим
. Тогда получим
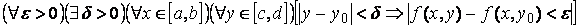 . Это означает, что функция
. Это означает, что функция 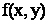 равномерно стремится к
равномерно стремится к 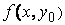 . В таком случае по теореме 3
. В таком случае по теореме 3 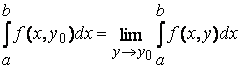 , а уже отсюда следует равенство
, а уже отсюда следует равенство 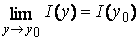 , то есть наша функция
, то есть наша функция 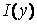 непрерывна на
непрерывна на 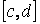 .
.
Замечание 4. Совершенно аналогично доказывается теорема для 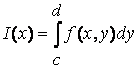 , где
, где  .
.
Следствие 2. Если 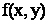 непрерывна на прямоугольнике
непрерывна на прямоугольнике 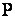 , то
, то 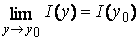 .
.
Циркуляция векторного поля. Циркуляция как работа в силовом поле
Циркуля́цией ве́кторного по́ля называется криволинейный интеграл второго рода, взятый по произвольному замкнутому контуру Γ. По определению
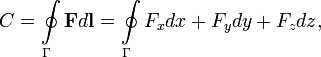
где 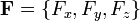 — векторное поле (или вектор-функция), определенное в некоторой области D, содержащей в себе контур Γ,
— векторное поле (или вектор-функция), определенное в некоторой области D, содержащей в себе контур Γ, 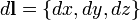 — бесконечно малое приращение радиус-вектора
— бесконечно малое приращение радиус-вектора 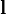 вдоль контура. Окружность на символе интеграла подчёркивает тот факт, что интегрирование производится по замкнутому контуру. Приведенное выше определение справедливо для трёхмерного случая, но оно, как и основные свойства, перечисленные ниже, прямо обобщается на произвольную размерность пространства.
вдоль контура. Окружность на символе интеграла подчёркивает тот факт, что интегрирование производится по замкнутому контуру. Приведенное выше определение справедливо для трёхмерного случая, но оно, как и основные свойства, перечисленные ниже, прямо обобщается на произвольную размерность пространства.
Свойства
Аддитивность
Циркуляция по контуру, ограничивающему несколько смежных поверхностей, равна сумме циркуляций по контурам, ограничивающим каждую поверхность в отдельности, то есть
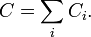
Формула Стокса
Циркуляция вектора F по произвольному контуру Г равна потоку вектора 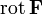 через произвольную поверхность S, ограниченную данным контуром.
через произвольную поверхность S, ограниченную данным контуром.
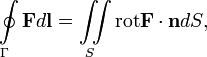
где 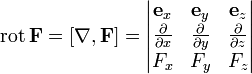 — ротор (вихрь) вектора F.
— ротор (вихрь) вектора F.
В случае, если контур плоский, например лежит в плоскости OXY, справедлива теорема Грина
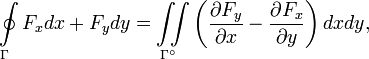
где 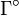 — плоскость, ограничиваемая контуром
— плоскость, ограничиваемая контуром 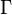 (внутренность контура).
(внутренность контура).
Если F — некоторое силовое поле, тогда циркуляция этого поля по некоторому произвольному контуру Γ есть работа этого поля при перемещении точки вдоль контура Г. Отсюда непосредственно следует критерий потенциальности поля: поле является потенциальным когда циркуляция его по произвольному замкнутому контуру есть нуль. Или же, как следует из формулы Стокса, в любой точке области D ротор этого поля есть нуль.
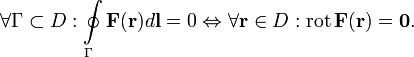
44. Поток векторного поля и его вычисление
Понятие потока векторного поля удобно рассматривать на примере потока жидкости, движущейся через некоторую поверхность. Объем жидкости, протекающей в единицу времени через поверхность, расположенную в движущейся жидкости, назовем потоком жидкости через эту поверхность.
Пусть поверхность S расположена в поле  скоростей частиц несжимаемой жидкости с плотностью ρ = 1. Можно показать, что поток векторного поля в этом случае равен
скоростей частиц несжимаемой жидкости с плотностью ρ = 1. Можно показать, что поток векторного поля в этом случае равен
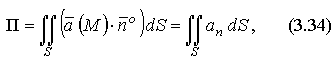
где 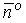 – единичный нормальный вектор к поверхности S, расположенный по одну сторону с вектором
– единичный нормальный вектор к поверхности S, расположенный по одну сторону с вектором  , а величина
, а величина 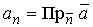 .
.
Независимо от физического смысла вектора  интеграл (3.34) по поверхности называют потоком векторного поля через поверхность S.
интеграл (3.34) по поверхности называют потоком векторного поля через поверхность S.
Пусть 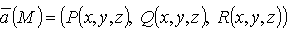 и
и 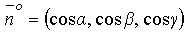 тогда поток П вектора
тогда поток П вектора  через поверхность S можно записать в виде:
через поверхность S можно записать в виде:
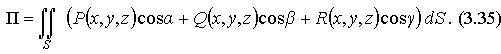
Или учитывая связь поверхностных интегралов первого и второго родов, можно записать поток П через поверхностный интеграл в координатах:
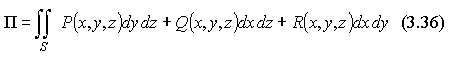
ПРИМЕР 1. Ориентированные поверхности.
Непосредственное вычисление потока. Поскольку поток векторного поля определен с помощью поверхностного интеграла, вычисление потока сводится к вычислению такого интеграла от функции 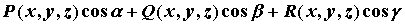 , где
, где 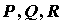 - компоненты векторного поля,
- компоненты векторного поля, 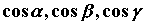 - направляющие косинусы вектора нормали.
- направляющие косинусы вектора нормали.
