Колебательные системы в биологии и медицине
Лекция №1
Колебания и волны
- Гармонический осциллятор. Колебательные системы в биологии и медицине.
- Механические волны, их уравнение. Вектор Умова. Ультразвук, его применение в медицине.
- Эффект Доплера, его медицинские приложения
1. Колебания гармонического осциллятора являются очень важным примером периодического движения. К числу классических систем, аналогичных гармоническому осциллятору, относятся любые системы, которые, будучи слегка выведены из положения равновесия, совершают устойчивые колебания. К ним относятся:
- Математический маятник в пределах малых углов отклонения.
- Масса на пружине в пределах малых амплитуд колебаний.
- Колебательный контур, состоящий из конденсатора и катушки.
Частота колебаний осциллятора не зависит от амплитуды.
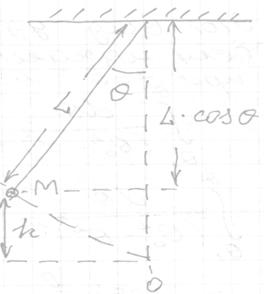
Математический маятник состоит из материальной точки массой m, расположенной на нижнем конце невесомого стержня длиной L, свободно вращающегося вокруг оси, проходящей через верхний конец.
Выведем уравнение колебаний маятника. Проще всего записать уравнение F=ma, однако поучительнее будет решить поставленную задачу через закон сохранения энергии. Отклонение маятника определяется углом  , который стержень образует с вертикалью.
, который стержень образует с вертикалью.
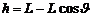 (1)
(1)
Потенциальная энергия маятника
U( 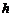 )=Mgh (2)
)=Mgh (2)
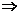
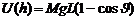 (3)
(3)
Кинетическая энергия маятника равна
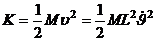 (4)
(4)
Полная энергия маятника равна 
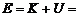
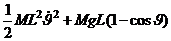 (5)
(5)
Принимая во внимание, что 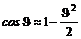 (6)
(6)
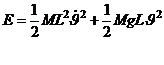 (7)
(7)
Решая это уравнение относительно 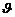 , находим:
, находим:
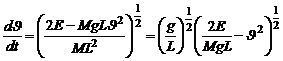 (8)
(8)
При 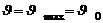
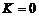 . Тогда из (7) получим с учетом того, что
. Тогда из (7) получим с учетом того, что 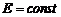 :
:
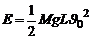 ,
, 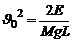 (9)
(9)
Тогда (8) перепишется в виде:
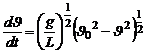 (10)
(10)
Или 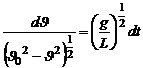 (11)
(11)
Этот вид удобен для интегрирования. Если начальные условия таковы, что при 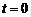
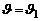 , то
, то
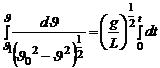 (12)
(12)
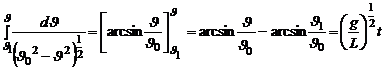 (13)
(13)
Так как 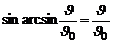 , то (13) запишется
, то (13) запишется
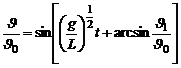 (14)
(14)
Или 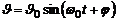 , (15)
, (15)
где 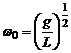 - круговая частота
- круговая частота
 -фаза колебаний
-фаза колебаний
Период колебаний математического маятника 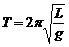
пружинного 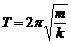
колебательного контура 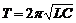
Примеры решения задач
1. Материальная точка массой 5 г. колеблется согласно уравнению 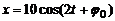 . Найти максимальную силу, действующую на точку и полную энергию.
. Найти максимальную силу, действующую на точку и полную энергию.
Решение
Сила, действующая на материальную точку, равна 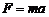 . Ускорение
. Ускорение 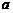 может быть найдено как вторая производная смещения
может быть найдено как вторая производная смещения 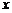 по времени. Первая производная
по времени. Первая производная 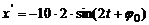 . Вторая производная
. Вторая производная 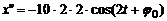 . Максимальное значение косинуса -1,
. Максимальное значение косинуса -1, 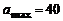 и
и 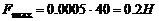
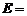
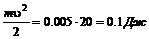
Механические волны
Механической волной называют механические возмущения, распространяющиеся в пространстве и несущие энергию.
Уравнение волны выражает зависимость смещения колеблющейся точки, участвующей в волновом процессе, от координаты ее равновесного положения и времени.
Пусть волна распространяется вдоль оси ОХ без затухания с амплитудой А. Зададим колебание точки с координатой х = 0 (источник колебаний) уравнением
 (1)
(1)
До точки с произвольной координатой х возмущение от начала координат дойдет через время 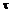 , поэтому колебания этой точки запаздывают:
, поэтому колебания этой точки запаздывают:

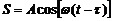 (2)
(2)
Так как 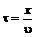 , то
, то 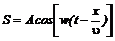 (3)
(3)
Волновой процесс связан с переносом энергии.
Поток энергии волн равен отношению энергии, перенесенной волнами через некоторую поверхность, ко времени, в течение которого эта энергия перенесена
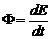 (4)
(4)
Интенсивность волн (вектор Умова) равна потоку энергии волн, отнесенному к площади, ориентированной перпендикулярно направлению распространения волн:
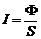 (5)
(5)
Примеры решения задач
1. Определить разность фаз в пульсовой волне между двумя точками артерии, расположенными на расстоянии 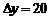 см друг от друга. Скорость пульсовой волны считать равной 10 м/с, а колебания сердца гармоническими с частотой 1,2 Гц
см друг от друга. Скорость пульсовой волны считать равной 10 м/с, а колебания сердца гармоническими с частотой 1,2 Гц
Решение
Длине волны соответствует разность фаз 2 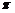 , а расстоянию
, а расстоянию 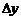 - разность фаз
- разность фаз 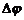 , которую следует найти. Составим пропорцию:
, которую следует найти. Составим пропорцию:
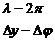
Отсюда 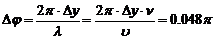

Ультразвук (УЗ)
Природа и свойства. УЗ – это механические колебания и волны с частотой от 20 кГц до 1010 Гц. Распространение УЗ в среде сопровождается его поглощением. Чем больше поглощение УЗ, тем меньше глубина его проникновения. Скорость распространения УЗ в жидкости 1500 м/с, в твердом теле - 4000 м/с.
При распространении УЗ волн имеют место их дифракция, интерференция, преломление и отражение. Отражение и преломление УЗ происходит на границе контакта сред, отличающихся по плотности.
Источники и приемники ультразвука. Для генерации УЗ применяют УЗ излучатели. Они бывают 2-х типов: механические и электромеханические. Наибольшее распространение получили электромеханические излучатели. Их действие основано на явлении обратного пьезоэлектрического эффекта – механической деформации тела под действием переменного электрического поля. Для приема используется явление прямого пьезоэлектрического эффекта, при котором УЗ колебания, попадая на поверхность пьезокристалла, вызывают его колебания, сопровождающиеся генерацией переменного электрического поля.
Воздействие УЗ на организм. УЗ влияет на скорость биохимических реакций, увеличивает проницаемость клеточных мембран, скорость диффузии, активирует обменные процессы. УЗ вызывает микровибрации на клеточном и субклеточном уровнях, разрушает клетки и микроорганизмы.
Применение УЗ для лечения
Тепловое действие УЗ широко применяется в физиотерапии для лечения воспалительных заболеваний: синуситов, гайморитов, бронхитов и т.д., для заживления ран, лечения трофических язв, рассасывания отеков и гематом, заживления костной ткани.
Эффективным средством лечения является фонофорез – введение в организм человека с помощью ультразвука жидких лекарственных препаратов.
С помощью УЗ скальпеля проводится рассечение ткани с одновременной коагуляцией сосудов. УЗ используется для дробления почечных камней (УЗ литотрипсия).
Эффект Доплера
Его суть заключается в изменении частоты звука, воспринимаемого наблюдателем, вследствие относительного движения источника и приемника звука. Когда звук отражается от движущегося объекта, частота отраженного сигнала изменяется (происходит сдвиг частоты).
Частота колебаний, воспринимаемых наблюдателем, определяется выражением
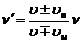 ,
,
где 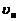 и
и 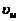 - скорости наблюдателя и источника упругой волны относительно среды,
- скорости наблюдателя и источника упругой волны относительно среды, 
- скорость распространения волны в этой среде, 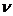 -частота испускаемых колебаний. Верхние знаки соответствуют встречному движению наблюдателя и источника, нижние - в противоположные стороны.
-частота испускаемых колебаний. Верхние знаки соответствуют встречному движению наблюдателя и источника, нижние - в противоположные стороны.
Доплеровский сдвиг частоты определяется выражением 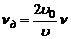 , где
, где 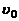 - скорость движущегося объекта,
- скорость движущегося объекта,  - скорость волны (ультразвука),
- скорость волны (ультразвука), 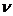 - частота сигнала.
- частота сигнала.
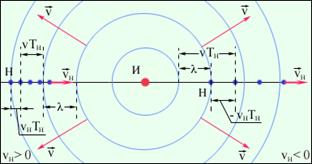 Эффект Доплера. Случай движущегося наблюдателя. Эффект Доплера. Случай движущегося наблюдателя. | 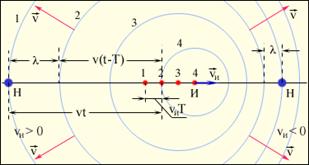 Эффект Доплера. Случай движущегося источника. Эффект Доплера. Случай движущегося источника. |
Примеры решения задач
1. Доплеровский сдвиг частоты при отражении ультразвукового импульса от движущихся эритроцитов равен 50 Гц. Частота излучения УЗ-сигнала равна 105 Гц. Определить скорость кровотока в сосуде.
Решение:
Как известно сдвиг частот при эффекте.Доплера представляет собой изменение частоты УЗ-сигнала при отражении от эритроцитов, т.е.
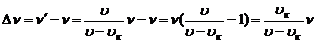 , здесь
, здесь 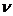 - частота излучения генератора,
- частота излучения генератора, 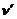 -частота сигнала, отраженного от эритроцитов,
-частота сигнала, отраженного от эритроцитов, 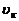 -скорость кровотока,
-скорость кровотока,  -скорость распространения УЗ в крови. Отсюда легко найти
-скорость распространения УЗ в крови. Отсюда легко найти 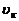 :
:

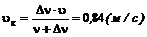
Лекция №2
Примеры решения задач
1. В широкой части горизонтальной трубы вода течет со скоростью 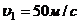 . Определить скорость течения воды в узкой части трубы, если разность давлений в широкой и узкой ее частях равна
. Определить скорость течения воды в узкой части трубы, если разность давлений в широкой и узкой ее частях равна 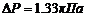
Решение:
Запишем уравнение Бернулли: 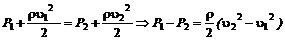
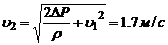
Формула Пуазейля
Наибольшей скоростью обладают частицы, движущиеся вдоль оси трубы; самый близкий к трубе слой жидкости неподвижен.
Для установления зависимости 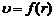 выделим мысленно цилиндрический объем жидкости радиуса r и длины l. На торцах этого цилиндра поддерживаются давления P1 и P2, что обуславливает результирующую силу:
выделим мысленно цилиндрический объем жидкости радиуса r и длины l. На торцах этого цилиндра поддерживаются давления P1 и P2, что обуславливает результирующую силу:
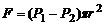 . (1)
. (1)
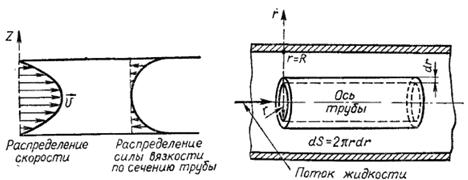
На боковую поверхность цилиндра со стороны окружающего слоя жидкости действует сила внутреннего трения, равная
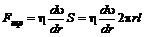 , (2)
, (2)
где 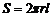 - площадь боковой поверхности цилиндра.
- площадь боковой поверхности цилиндра.
F=Fтр 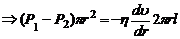 (3)
(3)
Знак (-), так как 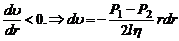 . (4)
. (4)
Проинтегрируем это уравнение:
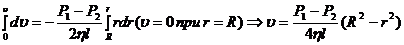 . (5)
. (5)
Наибольшую скорость имеет слой, текущий вдоль оси трубы (r=0):
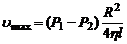
Определим объемную скорость течения жидкости Q. Для этого выделим цилиндрический слой радиусом r и толщиной dr. Площадь сечения этого слоя 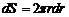 . За 1с слой переносит объем жидкости
. За 1с слой переносит объем жидкости
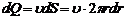 (6)
(6)
Подставим (5) в (6), получим:
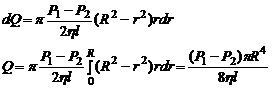 (7)
(7)
(7) - Формула Пуазейля
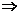 Через трубу протекает тем больше жидкости, чем меньше ее вязкость и больше радиус трубы.
Через трубу протекает тем больше жидкости, чем меньше ее вязкость и больше радиус трубы.
Формула Пуазейля аналогична закону Ома для участка цепи. Разность потенциалов соответствует разности давлений на концах трубы, сила тока - объемной скорости, электрическое сопротивление - гидравлическому сопротивлению:
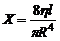 . (8)
. (8)
Гидравлическое сопротивление тем больше, чем больше вязкость 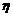 , длина l трубы и меньше сечение.
, длина l трубы и меньше сечение.
Примеры решения задач
1. При чуме артерия сужается в 2 раза. Во сколько раз изменится объемная скорость кровотока?
Решение
По формуле Пуазейля 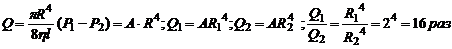
2. Каково гидравлическое сопротивление кровеносного сосуда длиной 0,12м и радиусом 0,1мм?
Решение:
Из формулы (8) для гидравлического сопротивления
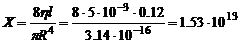
3. Модель кровообращения Франка
Модель позволяет установить связь между ударным объемом крови (объем крови, выбрасываемый желудочком за одну систолу), гидравлическим сопротивлением периферической части системы кровообращения х0 и изменением давления в артериях. Артериальная часть системы кровообращения моделируется упругим (эластичным) резервуаром (УР).
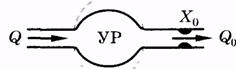
В УР (артерия) поступает кровь из сердца Q. От УР кровь оттекает со скоростью Q0 в периферическую систему (артериолы, капилляры). Объем крови в УР зависит от P:
V=V0+kP, (1)
где k - упругость резервуара;V0 - объем УР при P=0. Из (1)
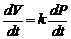 (2)
(2)
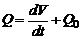 (3),
(3),
т.е. объемная скорость кровотока из сердца равна скорости возрастания объема УР, т.е. скорости оттока крови из упругого резервуара.
На основании формулы Пуазейля и формулы (3) можно записать для периферии:
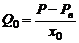 , (4)
, (4)
где P - давление в УР; Pв - венозное давление. При Pв = 0
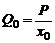 (5)
(5)
Подставляя (2) и (5) в (3), получим:
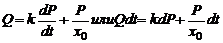 (6)
(6)
Во время систолы (сокращение сердца) происходит расширение УР, во время диастолы - отток крови к периферии, Q=0. Тогда (6) перепишется:
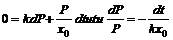 (7)
(7)
Проинтегрировав (9), получаем зависимость давления в УР после систолы от времени:
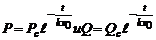 (8)
(8)
На основе механической модели по аналогии можно построить электрическую модель.
Здесь источник U переменного электрического напряжения служит аналогом сердца, выпрямитель В - сердечного клапана.
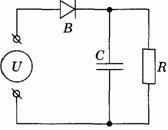
Конденсатор С в течение полупериода накапливает заряд, а затем разряжается на резистор R, так сглаживается сила тока через резистор. Действие конденсатора аналогично действию упругого резервуара, который сглаживает колебания давления крови в артериях и капиллярах. Резистор является электрическим аналогом периферической сосудистой системы.
Пульсовая волна - это распространяющаяся по аорте и артериям волна повышенного давления, вызванная выбросом крови из левого желудочка в период систолы.
Скорость пульсовой волны в крупных сосудах определяется формулой Моенса-Кортевега: 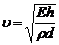 , где Е - модуль упругости,
, где Е - модуль упругости, 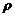 - плотность вещества сосуда, h - толщина стенки сосуда, d-диаметр сосуда.
- плотность вещества сосуда, h - толщина стенки сосуда, d-диаметр сосуда.
Примеры решения задач
1. Скорость пульсовой волны в артериях составляет 8 м/с. Чему равен модуль упругости этих сосудов, если известно, что отношение радиуса просвета к толщине стенки сосуда равно 6, а плотность крови равна 1150кг/м3?
Решение:
По формуле Моенса-Кортевега 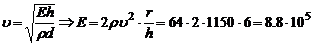
2. Определить среднюю линейную скорость кровотока в сосуде радиусом 1,5 см, если во время систолы через него протекает 60 мл крови. Длительность систолы считать равной 0,25с.
Решение:
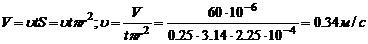
Лекция №3
Электростатика
1. Взаимодействие электрических зарядов в вакууме. Закон Кулона. Электрическое поле и его напряженность. Силовые линии электрического поля.
2. Электрический диполь. Поле диполя.
3. Теорема Остроградского-Гаусса.
4. Работа перемещения заряда в электрическом поле. Потенциал.
5. Использование электрических полей в медицине.
1. Электростатика изучает взаимодействие и условия равновесия покоящихся электрически заряженных тел, а также свойства этих тел, обусловленные электрическими зарядами.
Взаимодействие электрических зарядов осуществляется в соответствии с законом Кулона, который опытным путем установил, что два точечных заряда взаимодействуют в вакууме с силой F, пропорциональной величинам зарядов q1 и q2 и обратно пропорциональной квадрату расстояния r между ними и направленной по линии, соединяющей эти заряды:
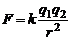 , (1)
, (1)
где k - коэффициент пропорциональности, 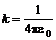 ,
, 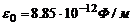 - электрическая постоянная. Таким образом
- электрическая постоянная. Таким образом
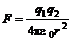 (2)
(2)
Электрическим полем называется вид материи, посредством которого взаимодействуют электрические заряды.
Напряженность электрического поля в данной точке есть вектор, равный по величине силе, действующей на единичный положительный заряд, помещенный в эту точку и совпадающий с ней по направлению:
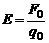 (3)
(3)
Е измеряется в В/м.
Силовой линией электрического поля называется линия, в каждой точке которой касательная совпадает с вектором напряженности поля.
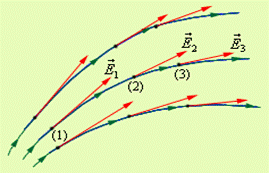
Электрическое поле называется однородным, если во всех его точках напряженность E одинакова. Напряженность электрического поля точечного заряда определяется формулой:
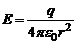 , (4)
, (4)
где r - расстояние от заряда, создающего поле, до точки, в которой определяется напряженность.
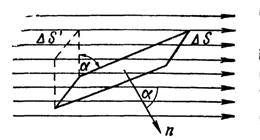
Число силовых линий, пронизывающих некоторую поверхность, расположенную в электрическом поле, называется потоком напряженности электрического поля N через эту поверхность:
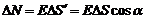 (5),
(5),
где 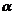 - угол между силовой линией и нормалью n к площадке
- угол между силовой линией и нормалью n к площадке 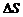 :
:
2. Электрический диполь. Поле диполя.
Электрическим диполем называется совокупность двух равных по величине разноименных точечных зарядов q, расположенных на некотором расстоянии друг от друга. Произведение P = ql называется моментом диполя, а l - его плечом. Дипольный момент направлен по оси диполя в сторону положительного заряда.
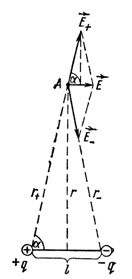
Напряженность поля на продолжении оси диполя
Напряженность поля вдоль оси диполя равна разности напряженностей Е+ и Е-, создаваемых положительным и отрицательным зарядами: Е = Е+ - Е-

Если r - расстояние от точки А до середины оси диполя, на основании (4) можно записать:
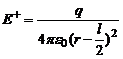 и
и 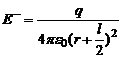 . Тогда
. Тогда 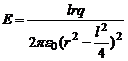
Полагая, что r >> l, пренебрежем 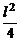 . Тогда
. Тогда 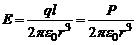 (6)
(6)
Напряженность поля на перпендикуляре к середине оси диполя.
Напряженность Е в точке А равна Е = Е+ + Е-. Так как r+ = r- , то Е+ = Е-, Тогда Е – диагональ ромба, 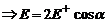 . Но
. Но 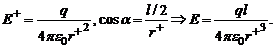
Полагая r>>l, r+ 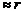
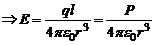 (7)
(7)
Таким образом, на большом расстоянии от диполя напряженность электрического поля диполя обратно пропорциональна кубу расстояния.
3. Теорема Остроградского-Гаусса.
Определим поток напряженности поля электрических зарядов q1, q2, … qn через некоторую замкнутую поверхность, окружающую эти заряды. Поток будем считать отрицательным, если он направлен внутрь поверхности, в противном случае – положительным
Рассмотрим сначала случай сферической поверхности радиусом R, окружающей один заряд q, находящийся в центре сферы. Согласно (4) напряженность поля на всей сфере одинакова и равна
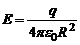 . (8)
. (8)
Силовые линии направлены по радиусам, т.е. перпендикулярно поверхности сферы. Это дает возможность применить для расчета потока напряженности N формулу
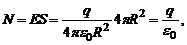 (9)
(9)
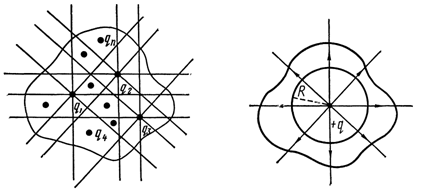
где 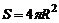 - площадь сферической поверхности.
- площадь сферической поверхности.
Окружим теперь сферу произвольной замкнутой поверхностью. Каждая силовая линия, пронизывающая сферу, пронижет и эту поверхность. Следовательно, формула (9) справедлива не только для сферы, но и для любой замкнутой поверхности.
В случае произвольной поверхности, окружающей n зарядов, поток напряженности через нее равен сумме потоков, создаваемых каждым из зарядов:
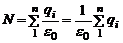 .
.
Таким образом, поток напряженности, пронизывающий любую замкнутую поверхность, окружающую электрические заряды, пропорционален алгебраической сумме окруженных зарядов.
Это положение называется теоремой Остроградского-Гаусса.
Лекция №4
Контактные явления
1. Контактная разность потенциалов. Законы Вольты.
2. Термоэлектричество.
3. Термопара, ее использование в медицине.
4. Потенциал покоя. Потенциал действия и его распространение.
- Контактная разность потенциалов. Законы Вольты.
При тесном соприкосновении разнородных металлов между ними возникает разность потенциалов, зависящая только от их химического состава и температуры (первый закон Вольты). Эта разность потенциалов называется контактной.
Для того чтобы покинуть металл и уйти в окружающую среду, электрон должен совершить работу против сил притяжения к металлу. Эта работа называется работой выхода электрона из металла.
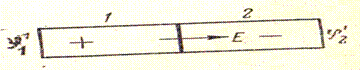
Приведем в контакт два различных металла 1 и 2, имеющих работу выхода соответственно A1 и A2, причем A1 < A2. Очевидно, что свободный электрон, попавший в процессе теплового движения на поверхность раздела металлов, будет втянут во второй металл, так как со стороны этого металла на электрон действует большая сила притяжения (A2 > A1). Следовательно, через контакт металлов происходит «перекачка» свободных электронов из первого металла во второй, в результате чего первый металл зарядится положительно, второй - отрицательно. Возникающая при этом разность потенциалов 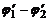 создает электрическое поле напряженностью Е, которое затрудняет дальнейшую «перекачку» электронов и совсем прекратит ее, когда работа перемещения электрона за счет контактной разности потенциалов станет равна разности работ выхода:
создает электрическое поле напряженностью Е, которое затрудняет дальнейшую «перекачку» электронов и совсем прекратит ее, когда работа перемещения электрона за счет контактной разности потенциалов станет равна разности работ выхода:
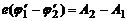 или
или
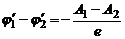 (1)
(1)
Приведем теперь в контакт два металла с A1 = A2, имеющие различные концентрации свободных электронов n01 > n02. Тогда начнется преимущественный перенос свободных электронов из первого металла во второй. В результате первый металл зарядится положительно, второй – отрицательно. Между металлами возникнет разность потенциалов 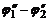 , которая прекратит дальнейший перенос электронов. Возникающая при этом разность потенциалов определяется выражением:
, которая прекратит дальнейший перенос электронов. Возникающая при этом разность потенциалов определяется выражением:
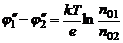 , (2)
, (2)
где k - постоянная Больцмана.
В общем случае контакта металлов, различающихся и работой выхода и концентрацией свободных электронов к.р.п. из (1) и (2) будет равна:
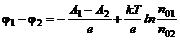 (3)
(3)
Легко показать, что сумма контактных разностей потенциалов последовательно соединенных проводников равна контактной разности потенциалов, создаваемой концевыми проводниками, и не зависит от промежуточных проводников:
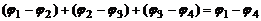 .
.
Это положение называется вторым законом Вольты.
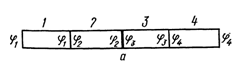
Если теперь непосредственно соединить концевые проводники, то существующая между ними разность потенциалов компенсируется равной по величине разностью потенциалов 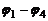 , возникающей в контакте 1 и 4. Поэтому к.р.п. не создает тока в замкнутой цепи металлических проводников, имеющих одинаковую температуру.
, возникающей в контакте 1 и 4. Поэтому к.р.п. не создает тока в замкнутой цепи металлических проводников, имеющих одинаковую температуру.
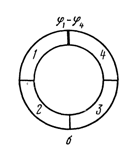
2. Термоэлектричество – это зависимость контактной разности потенциалов от температуры.
Составим замкнутую цепь из двух разнородных металлических проводников 1 и 2.
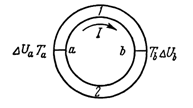
Температуры контактов a и b будем поддерживать различными Тa > Tb. Тогда, согласно формуле (3), к.р.п. в горячем спае больше, чем в холодном: 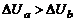 . В результате между спаями a и b возникает разность потенциалов
. В результате между спаями a и b возникает разность потенциалов 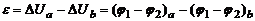 , называемая термоэлектродвижущей силой, а в замкнутой цепи пойдет ток I. Пользуясь формулой (3), получим
, называемая термоэлектродвижущей силой, а в замкнутой цепи пойдет ток I. Пользуясь формулой (3), получим
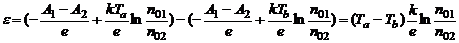 , или
, или
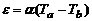 , (4)
, (4)
где 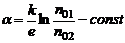 для каждой пары металлов.
для каждой пары металлов.
- Термопара, ее использование в медицине.
Замкнутая цепь проводников, создающая ток за счет различия температур контактов между проводниками, называется термопарой.
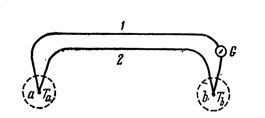
Из формулы (4) следует, что термоэлектродвижущая сила термопары пропорциональна разности температур спаев (контактов).
Формула (4) справедлива и для температур по шкале Цельсия: 
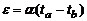 (4’)
(4’)
Термопарой можно измерить только разности температур. Обычно один спай поддерживается при 0ºС. Он называется холодным спаем. Другой спай называется горячим или измерительным.
Термопара обладает существенными преимуществами перед ртутными термометрами: она чувствительна, безинерционна, позволяет измерять температуру малых объектов, допускает дистанционные измерения.
Измерение профиля температурного поля тела человека.
Считается, что температура тела человека постоянна, однако это постоянство относительно, поскольку на различных участках тела температура не одинакова и меняется в зависимости от функционального состояния организма.
Температура кожи имеет свою вполне определенную топографию. Самую низкую температуру (23-30º) имеют дистальные отделы конечностей, кончик носа, ушные раковины. Самая высокая температура – в подмышечной области, в промежности, области шеи, губ, щек. Остальные участки имеют температуру 31 - 33,5 ºС.
У здорового человека распределение температур симметрично относительно средней линии тела. Нарушение этой симметрии и служит основным критерием диагностики заболеваний методом построения профиля температурного поля с помощью контактных устройств: термопары и термометра сопротивления.
4. Потенциал покоя. Потенциал действия и его распространение.
Поверхностная мембрана клетки не одинаково проницаема для разных ионов. Кроме того, концентрация каких-либо определенных ионов различна по разные стороны мембраны, внутри клетки поддерживается наиболее благоприятный состав ионов. Эти факторы приводят к появлению в нормально функционирующей клетке разности потенциалов между цитоплазмой и окружающей средой (потенциал покоя)
При возбуждении разность потенциалов между клеткой и окружающей средой изменяется, возникает потенциал действия, который распространяется в нервных волокнах.
Механизм распространения потенциала действия по нервному волокну рассматривается по аналогии с распространением электромагнитной волны по двухпроводной линии. Однако наряду с этой аналогией существуют и принципиальные различия.
Электромагнитная волна, распространяясь в среде, ослабевает, так как ее энергия рассеивается, превращаясь в энергию молекулярно-теплового движения. Источником энергии электромагнитной волны является ее источник: генератор, искра и т.д.
Волна возбуждения не затухает, так как получает энергию из самой среды, в которой она распространяется (энергия заряженной мембраны).
Таким образом, распространение потенциала действия по нервному волокну происходит в форме автоволны. Активной средой являются возбудимые клетки.
Примеры решения задач
1. При построении профиля температурного поля поверхности тела человека используется термопара с сопротивлением r1 = 4 Ом и гальванометр с сопротивлением r2 = 80 Ом; I=26 мкА при разности температур спаев 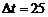 ºС. Чему равна постоянная термопары?
ºС. Чему равна постоянная термопары?
Решение:
Термоэдс, возникающая в термопаре, равна 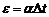 , где
, где 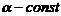 термопары,
термопары, 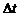 -разность температур спаев.
-разность температур спаев.
По закону Ома для участка цепи 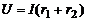 ,где U принимаем как
,где U принимаем как 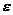 . Тогда
. Тогда 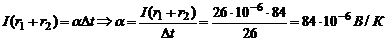
Лекция №5
Электромагнетизм
1. Природа магнетизма.
2. Магнитное взаимодействие токов в вакууме. Закон Ампера.
3. Напряженность магнитного поля. Формула Ампера. Закон Био-Савара-Лапласа.
4. Диа-, пара- и ферромагнитные вещества. Магнитная проницаемость и магнитная индукция.
5. Магнитные свойства тканей организма.
1. Природа магнетизма.
Вокруг движущихся электрических зарядов (токов) возникает магнитное поле, посредством которого эти заряды взаимодействуют с магнитными или другими движущимися электрическими зарядами.
Магнитное поле является силовым полем, его изображают посредством магнитных силовых линий. В отличие от силовых линий электрического поля магнитные силовые линии всегда замкнуты.
Магнитные свойства вещества обусловлены элементарными круговыми токами в атомах и молекулах этого вещества.
2. Магнитное взаимодействие токов в вакууме. Закон Ампера.
Магнитное взаимодействие токов изучалось с помощью подвижных проволочных контуров. Ампер установил, что величина силы 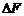 взаимодействия двух малых участков проводников 1 и 2 с токами пропорциональна длинам
взаимодействия двух малых участков проводников 1 и 2 с токами пропорциональна длинам 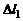 и
и 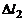 этих участков, силам тока I1 и I2 в них и обратно пропорциональна квадрату расстояния r между участками:
этих участков, силам тока I1 и I2 в них и обратно пропорциональна квадрату расстояния r между участками:
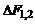 ~
~ 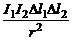 (1)
(1)
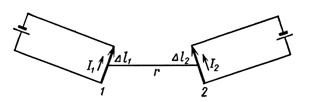
Выяснилось, что сила 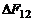 воздействия первого участка
воздействия первого участка 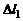 на второй
на второй 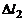 зависит от их взаиморасположения и пропорциональна синусам углов
зависит от их взаиморасположения и пропорциональна синусам углов 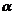 и
и 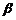 .
.
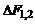 ~
~ 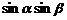 , (2)
, (2)
где 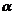 - угол между
- угол между 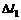 и радиусом-вектором r12, соединяющим
и радиусом-вектором r12, соединяющим 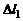 с
с 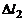 , а
, а 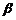 - угол между
- угол между 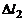 и нормалью n к плоскости Q, содержащей участок
и нормалью n к плоскости Q, содержащей участок 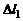 и радиус-вектор r12.
и радиус-вектор r12.
Объединяя (1) и (2) и вводя коэффициент пропорциональности k, получим математическое выражение закона Ампера:
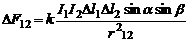 (3)
(3)
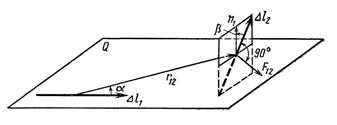
Направление силы 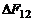 также определяется по правилу буравчика: оно совпадает с направлением поступательного движения буравчика, рукоятка которого вращается от
также определяется по правилу буравчика: оно совпадает с направлением поступательного движения буравчика, рукоятка которого вращается от 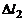 к нормали n1.
к нормали n1.
Элементом тока называется вектор, равный по величине произведению Idl бесконечно малого участка длины dl проводника на силу тока I в нем и направленный вдоль этого тока. Тогда, переходя в (3) от малых 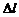 к бесконечно малым dl, можно записать закон Ампера в дифференциальной форме:
к бесконечно малым dl, можно записать закон Ампера в дифференциальной форме:
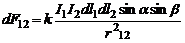 . (4)
. (4)
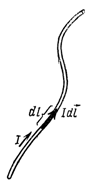
Коэффициент k можно представить в виде
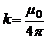 , (5)
, (5)
где 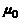 - магнитная постоянная (или магнитная проницаемость вакуума).
- магнитная постоянная (или магнитная проницаемость вакуума).
Величина 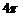 для рационализации с учетом (5) и (4) запишется в виде
для рационализации с учетом (5) и (4) запишется в виде
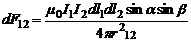 . (6)
. (6)
3. Напряженность магнитного поля. Формула Ампера. Закон Био-Савара-Лапласа.
Поскольку электрические токи взаимодействуют друг с другом посредством своих магнитных полей, количественную характеристику магнитного поля можно установить на основе этого взаимодействия-закона Ампера. Для этого проводник l с током I разобьем на множество элементарных участков dl. Он создает в пространстве поле.
В точке О этого поля, находящу
