Законы сохранения. Работа. Энергия
Примеры решения задач
11. Однородный цилиндр массой m = 10 кг и радиусом r = 5 см свободно скатывается без проскальзывания с наклонной плоскости высотой h = 1,0 м. Определить угловую скорость движения цилиндра с наклонной плоскости на горизонтальную плоскость. Начальная скорость цилиндра равна нулю.
| Дано: m = 10 кг r = 5,0 см h = 1,0 м | Решение  |
| а) ω –? б) L –? | |
В начальный момент движения скорость цилиндра равна нулю и его полная механическая энергия равна потенциальной  . При переходе на горизонтальную плоскость полная механическая энергия цилиндра равна сумме кинетической энергии
. При переходе на горизонтальную плоскость полная механическая энергия цилиндра равна сумме кинетической энергии  и потенциальной энергии
и потенциальной энергии  цилиндра. По закону сохранения полной механической энергии получается:
цилиндра. По закону сохранения полной механической энергии получается:
 (1)
(1)
Потенциальная энергия цилиндра определяется положением центра масс цилиндра над горизонтальной плоскостью. Поэтому:  , где g – ускорение свободного падения.
, где g – ускорение свободного падения.
Как известно, качение цилиндра по плоской поверхности можно рассматривать как поворот с угловой скоростью ω вокруг мгновенной оси вращения, проходящей по линии соприкосновения цилиндрической поверхности и плоскости. На рисунке мгновенная ось вращения проходит через точку М перпендикулярно плоскости рисунка. Следовательно, кинетическая энергия определяется выражением
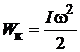 , (2)
, (2)
где I – момент инерции цилиндра относительно мгновенной оси вращения. Из известного выражения для момента инерции цилиндра относительно оси симметрии и теоремы Штейнера получается:
 . (3)
. (3)
Выражение (1) с учетом формул (2) и (3) принимает вид
 . (4)
. (4)
Из уравнения (4) для угловой скорости ω следует:
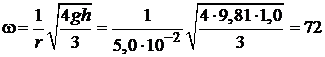 рад/с.
рад/с.
Момент импульса L при переходе цилиндра на горизонтальную плоскость направлен вдоль мгновенной оси вращения, как показано на рисунке. Модуль момента импульса
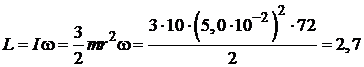 (кг×м²)/с.
(кг×м²)/с.
Ответ: ω = 72 рад/с; L = 2,7 (кг×м²)/с.
12. Два шара, один массой m1 = 2,0 кг, второй m2 = 3,0 кг, на горизонтальной плоскости движутся навстречу во взаимноперпендикулярных направлениях и сталкиваются абсолютно неупруго. Найти после соударения скорость шаров  , направление скорости и часть механической энергии шаров, перешедшей во внутреннюю энергию шаров. До соударения скорость первого шара
, направление скорости и часть механической энергии шаров, перешедшей во внутреннюю энергию шаров. До соударения скорость первого шара  = 5,0 м/с, второго
= 5,0 м/с, второго  = 3,0 м/с.
= 3,0 м/с.
Дано: m1 = 2,0 кг m2 = 3,0 кг 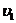 = 5,0 м/с = 5,0 м/с  = 3,0 м/с = 3,0 м/с | Решение   Рис. 1 Рис. 2 Рис. 1 Рис. 2 |
а)  –? б) α –? в) ΔW –? –? б) α –? в) ΔW –? |
На горизонтальной плоскости введем систему координат XOY, как показано на рис. 1. Соударение шаров происходит в начале системы координат. Соударение абсолютно неупругое, поэтому шары “слипаются” и движутся вместе со скоростью  , как показано на рис. 1. Внешняя сила (сила тяжести), действующая на шары, перпендикулярна к горизонтальной плоскости и, следовательно, выполняется закон сохранения импульса
, как показано на рис. 1. Внешняя сила (сила тяжести), действующая на шары, перпендикулярна к горизонтальной плоскости и, следовательно, выполняется закон сохранения импульса
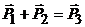 , (1)
, (1)
где 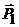 – импульс первого шара до соударения;
– импульс первого шара до соударения;  – импульс второго шара до соударения;
– импульс второго шара до соударения;  – импульс шаров после соударения. Из характера движения шаров и закона сохранения импульса следует, что направление векторов
– импульс шаров после соударения. Из характера движения шаров и закона сохранения импульса следует, что направление векторов  должны соответствовать рис. 2, а модули векторов связаны соотношением
должны соответствовать рис. 2, а модули векторов связаны соотношением  или
или
 (2)
(2)
Из уравнения (2) для скорости 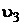 получаем:
получаем:
 м/с.
м/с.
Угол α, характеризующий направление скорости  , может быть найден из рис. 2 по формуле:
, может быть найден из рис. 2 по формуле:
 .
.
При абсолютно неупругом соударении механическая энергия тел уменьшается на величину ΔW, перешедшую во внутреннюю энергию шаров. Движение происходит на горизонтальной плоскости, поэтому механическая энергия системы обусловлена кинетической энергией шаров. Окончательно для величины ΔW следует

Ответ:  = 2,7 м/с; α = 42º; ΔW = 20 Дж.
= 2,7 м/с; α = 42º; ΔW = 20 Дж.
13. На скамье Жуковского вращается с частотой n1 = 1,0 об/с человек, держащий в центре горизонтально расположенный металлический стержень массой m = 5,0 кг и длиной l = 1,5 м. Определить частоту вращения человека n2 и совершенную работу A, если он повернет стержень в вертикальное положение. Момент инерции человека и скамьи I0 = 5,0 кг∙м².
| Дано: n1 = 1,0 об/с m = 5,0 кг l = 1,5 м I0 = 5,0 кг∙м2 | Решение Вращение человека со стержнем происходит вокруг вертикальной оси, момент внешних сил относительно которой равен нулю. Поэтому величина момента импульса L относительно вертикальной оси остается неизменной при повороте стержня, т. е.: 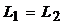 , или , или  (1) (1) |
| а) n2 –? б) A –? |
где I1 и ω1 – момент инерции и угловая скорость человека со стержнем, расположенным горизонтально; I2 и ω2 – момент инерции и угловая скорость человека со стержнем, расположенным вертикально. Угловая скорость ω и число оборотов в единицу времени связаны соотношением
 (2)
(2)
Момент инерции стержня Ic относительно оси, перпендикулярной к стержню и проходящей через его центр масс,  . Поэтому
. Поэтому
 (3)
(3)
При повороте стержня в вертикальное положение его момент инерции становится равным нулю. Следовательно,  (4) Подставляя соотношения (2) – (4) в формулу (1), получим:
(4) Подставляя соотношения (2) – (4) в формулу (1), получим:  . Отсюда для величины n2 следует:
. Отсюда для величины n2 следует:

 об/с.
об/с.
Работа A, совершенная человеком при повороте стержня, равна изменению кинетической энергии. Поэтому

Ответ: n2 = 1,2 об/с; A = 23 Дж.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1.44. Платформа в виде диска вращается по инерции около вертикальной оси с частотой n1 = 14 мин-1. На краю платформы стоит человек. Когда человек перешел в центр платформы, частота возросла до n2 = 25 мин-1. Масса человека m = 70 кг. Определить массу платформы. Момент инерции человека рассчитывать как для материальной точки.
(180 кг)
1.45. Человек массой m0 = 60 кг находится на неподвижной платформе массой m = 100 кг. С какой частотой n будет вращаться платформа, если человек будет двигаться по окружности радиусом r = 5,0 м вокруг оси вращения? Скорость движения человека относительно платформы u0 = 4,0 км/ч. Радиус платформы R = 10 м. Считать платформу однородным диском, а человека – точечной массой.
(0,49 об/мин)
1.46. Шар скатывается с наклонной плоскости высотой h = 90 см. Какую линейную скорость будет иметь шар в тот момент, когда он скатится с наклонной плоскости? Момент инерции шара J = 0,40 m×R2.
(3,6 м/c)
1.47. Два шара движутся навстречу друг другу вдоль оси Х. Масса первого шара m1 = 0,20 кг, масса второго шара m2 = 0,30 кг. До столкновения проекции скоростей шаров на ось  = 1,0 м/с,
= 1,0 м/с,  = -1,0 м/с. Найти проекции скоростей шаров
= -1,0 м/с. Найти проекции скоростей шаров  и
и  после центрального абсолютного упругого соударения.
после центрального абсолютного упругого соударения.
( 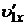 = -1,4 м/c;
= -1,4 м/c;  = 0,60 м/c)
= 0,60 м/c)
1.48. Тонкий однородный стержень длиной L может вращаться вокруг горизонтальной оси, проходящей через конец стержня перпендикулярно ему. Стержень отклонили на 90° от положения равновесия и отпустили. Определить скорость u нижнего конца стержня в момент прохождения равновесия.
(u = 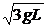 )
)
1.49. Тонкий однородный стержень длиной l и массой m может свободно вращаться вокруг горизонтальной оси, проходящей через один из его концов. Стержень устанавливают горизонтально и отпускают. Пренебрегая трением, определить угловую скорость стержня в момент прохождения им положения равновесия. Построить график зависимости углового ускорения стержня от угла между стержнем и горизонтом.
(w =  )
)
1.50. Сплошной однородный шар скатывается по наклонной плоскости длиной 5,0 м. Угол наклона плоскости к горизонту a = 30°. Определить скорость шара в конце наклонной плоскости, время движения шара до горизонтальной поверхности и качественно построить зависимость кинетической энергии шара как функцию времени. Потерями энергии пренебречь. Момент инерции шара относительно оси, проходящей через центр масс, J0 =  mR2 .
mR2 .
(u = 5,9 м/с; t = 1,7 c)
1.51. Сплошной цилиндр катится по горизонтальной поверхности в течение времени t = 3,0 c и останавливается, пройдя расстояние 9,0 м. Определить коэффициент трения, считая его постоянным. Построить качественно зависимость кинетической энергии тела как функцию времени движения.
(m = 0,31)
1.52. Вал массой m = 50 кг и радиусом R = 5,0 см вращался с частотой n = 10 об/с. К его цилиндрической поверхности прижали тормозную колодку с силой F = 30 Н, и через 8,0 с после начала торможения вал остановился. Определить коэффициент трения, считая его постоянным. Построить график зависимости угловой скорости и углового ускорения вала как функцию времени на интервале торможения.
(m = 0,33)
1.53. Шар и сплошной диск имеют одинаковые массы и катятся без проскальзывания по горизонтальной поверхности с одинаковыми постоянными скоростями. Кинетическая энергия шара W1 = 70 Дж. Определить кинетическую энергию диска W2. Найти отношение проекций момента импульса тел Lz1/Lz2 на мгновенную ось вращения, если R1/R2 = 0,7.
(W2 = 75 Дж; 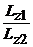 = 0,56)
= 0,56)
1.54. Тело массой М подвешено на нити длиной l. В тело попадает пуля массой m и застревает в нем, нить после этого отклоняется на угол a. Найти скорость пули. Считать, что вся масса тела М сосредоточена на расстоянии l от точки подвеса.
(u =  )
)
1.55. Сколько времени будет скатываться цилиндр с наклонной плоскости длиной l = 2,0 м и высотой h = 0,10 м, если считать, что проскальзывания нет? Качественно постройте зависимость кинетической Wk и потенциальной Wp энергии цилиндра как функцию времени.
(t = 3,5 c)
1.56. Два шара массами m1 = 10 кг и m2 = 15 кг подвешены на нитях длиной l = 2,0 м так, что шары соприкасаются между собой. Меньший шар был отклонен на угол j = 60° и отпущен. Определить высоту, на которую поднимутся оба шара после удара. Удар шаров считать неупругим.
(h = 0,16 м)
1.57. В цилиндр массой m1 = 3,0 кг и радиусом R = 10 см, покоящийся на плоскости, попадает пуля массой m2 = 9,0 г, летящая со скоростью u0 = 60 м/с. Пуля летит параллельно плоскости на высоте h = 0,12 м от нее и перпендикулярно образующей цилиндра. Считая удар абсолютно неупругим, найдите линейную скорость оси цилиндра, угловую скорость цилиндра. Проскальзыванием цилиндра пренебречь.
 (
(  рад/с;
рад/с;  = 0,14 м/с)
= 0,14 м/с)

 u0
u0 
1.58. Тела с массами m1 и m2 связаны невесомой и нерастяжимой нитью, которая переброшена через блок массой m, установленный на краю стола. Тело m1 находится на поверхности стола в закрепленном состоянии. Тело m2 свободно висит. В момент времени t = 0 тело m1 освободили, и вся система пришла в движение. Считая коэффициент трения между столом и телом m1 равным m, пренебрегая скольжением нити по блоку и трением в оси блока, найти работу сил трения за первые t секунд после начала движения. Блок считать однородным диском.
(  )
)
1.59. Стальной шарик массой m = 8 г, летящий горизонтально со скоростью 600 м/с, попадает в брусок массой M = 4m, прикрепленный к стенке пружиной с жесткостью k = 24 кН/м. Считая, что траектория шарика перпендикулярна поверхности бруска и совпадает с осью пружины, определить величину максимального сжатия пружины, если ударение было:
1) абсолютно неупругим; 2) абсолютно упругим.
Записать закон изменения деформации пружины как функцию от времени для случаев 1 и 2.
(  = 15 см;
= 15 см;  = 28 см)
= 28 см)
1.60. Поршень, закрепленный на пружине жесткостью k = 10 кН/м, после застревания в нем горизонтально летевшей со скоростью u = 520 м/с пули массой 20 г сместился на х = 8 см. Определить массу поршня М, если сила трения его о стенки цилиндра составляет 900 Н.
(M = 0,5 кг)
1.61. Нить с подвешенным на ней грузом отклонили на угол a и отпустили. На какой угол b отклонится нить с грузом, если при своем движении будет задержана штифтом, поставленным по вертикали посередине нити? Построить качественную зависимость скорости груза от времени, полагая, что потери энергии в системе не происходит.
(  )
)
1.62. Хоккейная шайба, имея начальную скорость u = 5,0 м/с, проходит до удара о борт площадки путь S = 10 м. Коэффициент трения шайбы о лед 0,10. Считая удар о борт абсолютно упругим и пренебрегая сопротивлением воздуха, определить, какой путь пройдет шайба после удара. Построить график зависимости ux = f(x), полагая положительное направление оси ОХ к борту.
(S1 = 2,7 м)
1.63. Человек стоит на неподвижной тележке и бросает горизонтально камень массой m1 = 2,0 кг со скоростью u = 8,0 м/с. Определить, какую работу А совершает при броске человек, если масса тележки с человеком m2 = 140 кг. Постройте график зависимости работы A = f(m2), если m2 – величина переменная.
(А = 63 Дж)
1.64. Гимнаст "крутит солнце" на перекладине. Считая, что вся масса гимнаста m сосредоточена в его центре масс и скорость гимнаста в верхней точке равна нулю, определить силу, действующую на руки гимнаста в низшей точке. Построить график зависимости вертикальной составляющей скорости гимнаста от времени uy = f(t). За начало отсчета принять верхнее положение гимнаста. Трением пренебречь.
(F = 5mg)
