Основные географические точки линии и круги на земном шаре.

Форма и размеры Земли

Поверхность, ограничивающая Землю как физическое тело, называется физической поверхностью Земли. Эта поверхность носит сложный нерегулярный характер, обусловленный неровностями рельефа: горами, равнинами, впадинами. На такой поверхности ввести какую-либо приемлемую для практики систему координат невозможно, поэтому эту поверхность необходимо «сгладить». Для этого используется понятие уровенной поверхности.

Уровенная поверхность – поверхность, во всех точках перпендикулярная направлению силы тяжести (отвесной линии).

В качестве сглаженной фигуры Земли разумно выбрать форму уровенной поверхности, совпадающей с физической поверхностью в морях и океанах, где нет неровностей рельефа. Такая фигура получила название геоида.

Геоид – фигура, образованная уровенной поверхностью, совпадающей в морях и океанах с их средней поверхностью.

В районах материков поверхность геоида проходит под уровнем рельефа местности. Эта поверхность называется средним уровнем моря, от которого отсчитывается высота рельефа и другие высоты. В России за начало уровня отсчета высот принято нулевое деление футштока (мерной линейки), установленной в Обводном канале г. Кронштадта.

Поверхность геоида хотя и является гладкой по сравнению с физической поверхностью Земли, но все же имеет неправильную форму (рис. 1.1). Геоид не имеет простого математического описания. Поэтому для упрощения вычислений расстояний и направлений его заменяют эллипсоидом вращения, который имеет правильную геометрическую форму и незначительно отличается от геоида.

Рис. 1.1. Поверхность геоида

Для удобства навигационных расчетов форму Земли представляют в виде шара с незначительным сжатием у полюсов. Этот эллипс имеет следующие размеры: экваториальный радиус а = 6378 км, полярный радиус b = 6357 км (рис. 1.2).

В воздушной навигации в большинстве случаях сжатием Земли пренебрегают и принимают Землю условно за шар, радиус которого составляет 6371 км.

Рис. 1.2. Земной элипсоид

Виды скоростей полета

В самолетовождении различают воздушную и путевую скорости.

Воздушная скорость (V) – скорость перемещения воздушного судна относительно воздушной среды.

Эту скорость воздушное судно приобретает под действием силы тяги двигателей. Воздушная скорость зависит от аэродинамических качеств самолета, его полетного веса и плотности воздуха, ветер не оказывает влияния на ее величину. Различают приборную и истинную воздушную скорость.

Истинная скорость (V_и) – действительная скорость самолета относительно воздушной среды на любой высоте. От нее зависит дальность, продолжительность и экономичность полета. Истинная скорость используется для решения многих навигационных задач, в частности, является элементом навигационного треугольника скоростей.

Приборная скорость (V_пр) – воздушная скорость, измеренная по прибору без учета погрешностей.

Приборная скорость зависит от воздушной скорости и массовой плотности воздуха. Массовая плотность воздуха прямо пропорциональна барометрическому давлению воздуха и обратно пропорциональна температуре воздуха. Таким образом, при одинаковой воздушной скорости на разных высотах либо при различной температуре на одинаковой высоте приборная скорость различна. Скоростной напор определяет подъемную силу крыла, поэтому ограничения по скорости задаются именно в приборной скорости как по нижнему пределу, так и по верхнему, в наборе высоты и на снижении скорость выдерживается также по приборной скорости, выпуск и уборка посадочной механизации производится тоже по приборной скорости.

Измерение воздушных скоростей осуществляется аэрометрическим методом,т. е. путем измерения давлений. Аэрометрический метод основан на уравнении Д. Бернулли, которое выражает закон сохранения энергии применительно к струйке газа (воздуха), обтекающего приемник воздушного давления.

Поскольку тарировка указателя скорости производится для условий полета на уровне моря при стандартных значениях температуры и давления воздуха, то только в этих условиях приборная скорость равна истинной воздушной. Разность между приборной и истинной скоростями растет и на высотах, равных 8–10 км, может достигать 50–70 %.

Комбинированные указатели скорости имеют две стрелки: широкая стрелка индицирует приборную скорость, а узкая – скорость, которая незначительно отличается от истинной скорости.

Путевая скорость (W) – скорость перемещения воздушного судна относительно земной поверхности.

Путевая скорость зависит от воздушной скорости, скорости и направления ветра.

Вектор истинной скорости совпадает с продольной осью ВС. Вектор путевой скорости совпадает с линией фактического пути.

Путевая скорость определяется по пройденному расстоянию и времени полета по формуле

W = .

На НЛ-10М путевую скорость можно определить, используя шкалы 1 и 2 (рис. 5.4).

Если пройденное расстояние выражено в километрах, а время полета в минутах, то путевую скорость следует отсчитывать против треугольного индекса. Если пройденное расстояние небольшое и время полета выражено в секундах, то путевую скорость следует отсчитывать против круглого индекса.

Рис. 5.4. Ключи для определения путевой скорости на НЛ-10М

Ветер и его характеристики

Воздушные массы постоянно движутся относительно земной поверхности в горизонтальном и вертикальном направлениях. Горизонтальное движение воздушных масс называется ветром. Ветер характеризуется скоростью и направлением. Скорость и направление изменяются с течением времени, с переменой места и с изменением высоты.

Для обеспечения точного самолетовождения необходимо учитывать влияние ветра иа полет самолета. С увеличением высоты в большинстве случаев скорость ветра увеличивается, а направление изменяется. На больших высотах, на которых выполняются полеты самолетов с ГТД, скорость ветра может достигать 200–300 км/чи более. В полете ветер определяется штурманом или пилотом путем соответствующих промеров и расчетов. Различают два вида направления ветра: навигационное и метеорологическое.

Навигационным направлением ветраназывается угол, заключенный между северным направлением магнитного меридиана и направлением в точку, куда дует ветер. НВ отсчитывается от северного направления магнитного меридиана по ходу часовой стрелки от 0 до 360° (рис. 8.1).

Рис. 8.1. Ветер навигационный и метеорологический

Метеорологическим направлением ветра (δ)называется угол, заключенный между северным направлением меридиана и направлением из точки, откуда дует ветер. Обычно на метеостанции отсчитывают метеорологическое направление ветра относительно северного направления истинного меридиана, т. е. угол δ_и.

В целях упрощения расчетов экипажам, производящим взлет и посадку, сообщается метеорологическое направление ветра у Земли, отсчитанное относительно магнитного меридиана, т. е. на метеостанции вводят поправку на магнитное склонение, если оно равно более 10°.

Направление ветра на высотах полета, отсчитанное от истинного меридиана, летный состав самостоятельно переводит в направление ветра, отсчитанное относительно магнитного меридиана. Метеорологическое направление ветра определяется по формуле

δ = δ_и – (±Δм).

Магнитное склонение (Δм) берется для района расположения метеостанции.

В штурманских расчетах используется навигационное направление ветра. Перевод метеорологического направления ветра в навигационное и обратно выполняется по следующим формулам:

НВ = δ ± 180°; δ = НВ ± 180°.

Знак «+» ставится, если δ или НВ меньше 180°, знак «–» – если δ или НВ больше 180°.

Скоростью ветра (U) называется скорость движения воздушных масс относительно земной поверхности. Скорость ветра измеряется в километрах в час или в метрах в секунду. Чтобы перейти от одних единиц измерения к другим, например, от метров в секунду к километрам в час, необходимо скорость ветра в метрах в секунду умножить на 3,6, т. е.:

U км/ч = U м/с × 3,6.

Перевод скорости ветра, выраженной в метрах в секунду, в скорость, выраженную в километрах в час, можно осуществлять подсчетом в уме по упрощенной формуле:

.

При штурманских расчетах для перехода от скорости ветра в метрах в секунду к скорости его в километрах в час и обратно пользуются НЛ-10М (рис. 8.2).

Рис. 8.2. Ключи для перевода единиц измерения скорости ветра на НЛ-10М

Пример

ЗМПУ = 100°; δ = 40°. Определите, в какую сторону направлен снос самолета и какова его путевая скорость.

Решение

1. Находим угол ветра:

УВ = δ ± 180° – ЗМПУ = 40° + 180° – 100° = 120°.

2. Определяем знак угла сноса и путевую скорость. Так как УВ находится в пределах от 0 до 180°, то угол сноса будет положительный, а путевая скорость меньше воздушной.

Максимальным углом сносаназывается угол сноса при углах ветра 90 и 270° (см. рис. 8.5). Его величина определятся по формуле

.

При современных скоростях полета величина УС обычно не превышает 10–20°. Известно, что синусы малых углов можно принять равными самим углам, выраженным в радианах. 1 рад = 57°,3 или округленно 60°.

На основании этого можно записать, что

.

Следовательно,

, откуда .

Из формулы видно, что УС тем больше, чем меньше воздушная скорость полета и чем больше скорость ветра.

Пример

V = 360 км/ч; U = 60 км/ч. Определите максимальный угол сноса.

Решение

.

Обычно максимальный угол сноса рассчитывается с помощью линейки НЛ-10М (рис. 8.7).

Рис. 8.7. Ключ для определения максимального угла сноса на НЛ-10М

24)Зависимость угла сноса и путевой скорости от воздушной скорости самолета следующая.

При неизменном ветре и курсе самолета путевая скорость изменяется соответственно изменению воздушной скорости, т. е. с увеличением воздушной скорости путевая скорость становится больше, а с уменьшением – меньше. Изменение воздушной скорости вызывает пропорциональное изменение путевой скорости, т. е. насколько изменилась воздушная скорость, настолько соответственно изменится и путевая скорость.

Угол сноса с возрастанием воздушной скорости уменьшается, а с ее уменьшением – увеличивается.

25)Зависимость угла сноса и путевой скорости от скорости ветра следующая.

При постоянной воздушной скорости и курсе самолета с увеличением скорости ветра угол сноса увеличивается, а при ее уменьшении – уменьшается (рис. 8.4).

Путевая скорость при попутном и попутно-боковом ветре с изменением скорости ветра изменяется так же, как и угол сноса. При встречном и встречно-боковом ветре с увеличением скорости ветра путевая скорость уменьшается.

Рис. 8.4. Зависимость угла сноса и путевой скорости от скорости ветра:

а – ветер попутно-боковой; б – ветер встречно-боковой

23)Зависимость угла сноса и путевой скорости от угла ветра следующая.

Угол ветра в полете не остается постоянным. Его величина изменяется в полете как вследствие изменения направления ветра, так и вследствие изменения направления полета.

Отложим в определенном масштабе вектор воздушной скорости (рис. 8.5). Из конца этого вектора радиусом, равным скорости ветра, в том же масштабе, опишем окружность. Если перемещать вектор ветра по ходу часовой стрелки, то угол ветра будет изменяться.

С помощью НЛ-10М

Решить навигационный треугольник скоростей – значит по его известным элементам найти неизвестные. Решение навигационного треугольника скоростей можно осуществить:

– графически (на бумаге);

– с помощью НЛ-10М, навигационного расчетчика или ветрочета;

– приближенно подсчетом в уме.

Навигационный треугольник скоростей представляет собой обычный косоугольный треугольник и может быть решен по теореме синусов:

.

Так как sinφ = sin (180°– φ), а внешний угол треугольника равен сумме внутренних углов, не смежных с ним, т. е. угол 180° – φ = УВ + УС, приведенные отношения записываются в следующем виде:

.

Эти отношения решаются с помощью НЛ-10М (рис. 8.8). При этом необходимо помнить:

– при углах ветра 0–180° углы сноса положительные;

– при углах ветра 180–360° углы сноса отрицательные;

– при углах ветра больше 180° на НЛ-10М устанавливают его дополнение до 360°, т. е. разность 360°– УВ;

– при угле ветра, равном нулю, W = V + U,апри угле ветра, равном 180°, W = V – U;для других значений углов ветра путевая скорость отсчитывается по НЛ-10М против суммы (УВ + УС), при нахождении которой к УВ прибавляется всегда абсолютная величина УС независимо от его знака;

– для углов ветра в пределах 5–175° используется шкала синусов, а в пределах 0,5–5 и 175–179,5° – шкала тангенсов.

Рис. 8.8. Ключ для определения угла сноса и путевой скорости на НЛ-10М

Отсчет угла сноса для расчета курса следования производится с точностью до 1°, а для точного определения путевой скорости при углах ветра, близких к 0 и 180°, – с точностью до десятых долей градуса;

При помощи НЛ-10М определяются угол сноса и путевая скорость,а затем рассчитываются курс и время полета на заданном участке трассы.

Курсом следования (МК_сл) называется курс, рассчитанный с учетом угла сноса для следования по линии заданного пути. Для каждого участка трассы полета курс следования, угол сноса и путевая скорость перед полетом определяются по прогностическому, а в полете по измеренному ветру.

Пример

V_и = 460 км/ч;ЗМПУ = 105°; δ = 330°; U = 80 км/ч; S = 120 км.Определите УС, W,МК_сл и t.

Решение

1. Находим угол ветра:

УВ = δ ± 180° – ЗМПУ = 330° – 180° – 105° = 45°.

2. Определяем угол сноса и путевую скорость с помощью НЛ-10М (см. рис. 8.8):

УС = +7°; W = 512 км/ч.

3. Рассчитываем магнитный курс следования:

МК_сл = ЗМПУ – (± УС) = 105° – (+ 7°) = 98°.

4. Определяем время полета с помощью НЛ-10М: t = 14 мин.

27)Определение скорости и направления ветра в полете осуществляется с помощью НЛ-10М, если известны угол сноса, путевая и воздушная скорости, магнитный курс самолета. Для решения этой задачи рассмотрим навигационный треугольник скоростей.

Из конца вектора воздушной скорости опустим на линию пути перпендикуляр (см. рис. 8.3). Величина путевой скорости может быть представлена в виде суммы двух отрезков: ОВ и ВС,т. е. W = OB + ВС, откуда отрезок ВС = W – ОВ.

Из прямоугольного треугольника ОАВ следует, что отрезок ОВ = VсоsУС. Так как косинусы малых углов примерно равны 1, то отрезок ОВ можно принять равным V(OB » V). Подставляя значение ОВ в выражение для отрезка ВС, получаем: ВС= W – V = ΔU.

Из прямоугольных треугольников АВО и ABC имеем:

АВ = VtgУС = ΔUtgУВ или VtgУC= ΔUtgα.

Запишем это равенство в виде следующей пропорции, имея в виду ее основное свойство:

.

Решая эту пропорцию на НЛ-10М, по шкалам 4 и 5 можно определить угол α (рис. 8.9), заключенный между линией фактического пути и метеорологическим направлением ветра. Этот угол измеряется от 0 до 90°. Зная величину угла α и используя шкалы 3 и 5 НЛ-10М, по теореме синусов определим скорость ветра (рис. 8.10).

Рис. 8.9. Ключ для определения угла б на НЛ-10М	Рис. 8.10. Ключ для определения скорости ветра на НЛ-10М

Направление ветра рассчитывается по формулам:

δ = ФМПУ + (± α) ± 180° при W > V_и;

δ = ФМПУ – (±α) при W < V_и.

Первой формулой пользуются, когда путевая скорость меньше воздушной, т. е. при встречно-боковом ветре, а второй – при попутно-боковом ветре, когда путевая скорость больше воздушной. Угол α берется со знаком, аналогичным углу сноса.

Для быстрого и правильного определения метеорологического направления ветра и его скорости необходимо запомнить следующие правила:

1. При попутном ветре (УС = 0°, α = 0°) путевая скорость больше воздушной скорости):

δ = ФМПУ ± 180°; U = W – V_и.

2. При встречном ветре (УС = 0°, α = 0°) путевая скорость меньше воздушной скорости):

δ = ФМПУ; U = V_и – W.

3. При боковом ветре (W » V_и, α = 90°) путевая скорость равна воздушной скорости):

δ = ФМПУ – (±90°).

4. При встречно-боковом ветре (W < V_и):

δ = ФМПУ – (± α).

5. При попутно-боковом ветре (W > V_и):

δ = ФМПУ + (± α) ± 180º

Пример

V_и = 450 км/ч;МК_сл = 50°; УС = + 7°; W = 490 км/ч.Определите направление и скорость ветра.

Решение

1. Находим разность между путевой и истинной воздушной скоростью:

ΔU = W – V_и= 490 – 450 = + 40 км/ч.

Ветер попутно-боковой.

2. Определяем угол αс помощью НЛ-10М (см. рис. 8.9): α =+ 54°.

3. Находим скорость ветра с помощью НЛ-10М (см. рис. 8.10): U = 68 км/ч.

4. Определяем ФМПУ и метеорологическое направление ветра:

ФМПУ = МК + (± УС) = 50° + (+ 7°) = 57°;

δ = ФМПУ + (±α) ± 180° = 57° + (+ 54°) + 180° = 291°.

Для упрощения выполнения некоторых навигационных расчетов пользуются понятием эквивалентного ветра.

Эквивалентным ветром (U_э)называется условный ветер, направление которого всегда совпадает с ЛЗП, а его скорость в сумме с воздушной скоростью дает такую же путевую скорость, как и действительный ветер.

Эквивалентный ветер определяется по специальной таблице, которая помещается в РЛЭ каждого типа самолета. Приближенно эквивалентный ветер можно определить по формуле

U_э » UсоsУВ.

Подсчетом в уме

Подсчетом в уме можно определить угол сноса, путевую скорость и курс следования, а также направление и скорость ветра по известным значениям воздушной и путевой скоростей, магнитному курсу и углу сноса.

Угол сноса и путевую скорость можно определить, пользуясь формулами

,

по которым рассчитывается таблица значений углов сноса и путевых скоростей для основных углов ветра (табл. 3). Эту таблицу необходимо знать на память.

Таблица 3

Пример

V_и = 450 км/ч;ЗМПУ=_;120°; δ = 30°; U = 60 км/ч.Определите угол сноса, курс следования и путевую скорость.

Решение

1. Находим угол ветра:

УВ = δ ± 180° – ЗМПУ = 30° + 180° – 120° = 90°.

2. Определяем угол сноса. Так как угол ветра равен 90°, то УС = УС_max:

УС_max = = +8°.

3. Определяем путевую скорость самолета. Поскольку ветер боковой, W » V_и = 450 км/ч.

4. Определяем курс следования:

МК_сл = ЗМПУ – (±УС) = 120° – (+ 8°) = 112°.

Направление и скорость ветра при попутном ветре, когда УС = 0°, а путевая скорость больше воздушной скорости, определяются по формулам

δ = ФМПУ ± 180°; U = W – V_и.

При встречном ветре, когда УС = 0°, а путевая скорость меньше воздушной скорости, направление и скорость ветра определяются по формулам

δ = ФМПУ; U = V_и– W.

При боковом ветре, когда угол сноса положительный (α = +90°) или отрицательный (α = –90°), а путевая скорость равна воздушной скорости, направление и скорость ветра определяются по формулам

δ = ФМПУ-(±90°); U = .

Пример

МК_сл = 202°; УС = –12°; V_и = 450 км/ч; W = 450 км/ч.Определите направление и скорость ветра.

Решение

1. ФМПУ = МК + (±УС) = 202° + (–12°) = 190°.

2. Определяем направление ветра:

δ = ФМПУ – (± α) = 190° – (–90°) = 280°.

3. Находим скорость ветра:

28)Всемирное координированное время(UTC) – атомное время, откорректированное в целях максимального его приближения к среднему солнечному времени гринвичского меридиана; используется в качестве общепризнанного международного стандарта часового времени.

Поясное время (Т_п) – солнечное местное время среднего меридиана часового пояса.

Местное время (Т_м) – время на данном географическом меридиане. Местным временем пользоваться в повседневной жизни неудобно, т. к. даже в различных районах одного большого города оно отличается на некоторую величину, и поэтому увязать его в повседневной жизни, работе транспорта и связи очень трудно. Поэтому в 1884 г. была принята система времени по часовым поясам. Сущность поясного времени заключается в том, что весь земной шар разделен на 24 часовых пояса – от нулевого до 23-го включительно.

Каждый пояс содержит 15° долготы или 1 ч по времени.

Часовой пояс, средний меридиан которого проходит через Гринвичскую обсерваторию, принято считать нулевым.

Долгота среднего меридиана нулевого часового пояса равна 0°; долгота среднего меридиана первого часового пояса – 15° в.д.; второго – 30° в.д. и так далее через каждые 15°.

Полет на радиостанцию

Полет на радиостанцию может быть выполнен пассивным, курсовым и активным способами. Основным из них является активный, позволяющий лететь точно по ЛЗП. Пеленги, определяемые при полете на радиостанцию, можно использовать для контроля пути по направлению.

Контроль пути по направлению при полете на радиостанцию выполняют путем сравнения МПР с ЗМПУ и определения дополнительной поправки в курс. Если МПР = ЗМПУ, то ВС находится на ЛЗП, если МПР меньше ЗМПУ, то ВС находится правее ЛЗП, если МПР больше ЗМПУ, то ВС находится левее ЛЗП (рис. 10.6).

Рис. 10.6. Контроль пути по направлению при полете на радиостанцию

Магнитный пеленг радиостанции определяется по формуле

МПР = МК + КУР.

Дополнительная поправка в курс, боковое уклонение и фактический угол носа определяются по формулам

ДП = МПУ – МПР; БУ = ДП; УС_ф = (±УС_р) + (±БУ).

Значение бокового уклонения и поправки в курс можно определить с помощью НЛ-10М (рис. 10.7).

Рис. 10.7. Ключ для определения БУ и ПК

Пример

ЗМПУ = 40°; МК_р = 35°; КУР = 10°; S_пр = 70 км; S_ост = 43 км. Определите МПР, ДП, БУ, УС_ф.

Решение

1. Находим магнитный пеленг радиостанции:

МПР = МК + КУР = 35° + 10° = 45°.

2. Определяем дополнительную поправку в курс:

ДП = ЗМПУ – МПР = 0° – 45° = –5°.

3. Рассчитываем боковое уклонение и фактический угол сноса:

БУ = ДП = 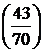(–5°) = –3°;

УС_р = ЗМПУ – МК_р = 40° – 35° = +5°;

УС_ф = (±УС_р) + (± БУ) = (+5°) + (–3°) = +2°.

Полет на радиостанцию пассивным способомнаиболее простой по выполнению. Необходимо выдерживать стрелку указателя АРК на значении КУР = 0 в течение всего полета до выхода на радиостанцию. Продольная ось ВС должна быть постоянно направлена на радиостанцию, МК = МПР. Пассивный полет на радиостанцию выполняется в следующем порядке:

1. Настроить радиокомпас на радиостанцию, прослушать позывной и убедиться в ее работе.

2. Доворотом ВС устанавить стрелку указателя на КУР = 0; пилотировать ВС так, чтобы стрелка указателя была на КУР = 0 (рис. 10.8).

Рис. 10.8. Пассивный полет на радиостанцию

3. Определить момент пролета радиостанции по расчету времени и по изменению КУР на 180°.

При боковом ветре фактический путь ВС будет иметь вид кривой, которая называется радиодромией. Ее форма зависит от воздушной скорости, скорости ветра, угла ветра и исходного удаления ВС от радиостанции. Отклонение радиодромии от ортодромии тем больше, чем меньше отношение скоростей . При п = 5–7 максимальное линейное боковое уклонение ВС от ортодромии (ЛЗП) составляет 5–7 % от исходного расстояния S, с которого был начат полет:

.

Полет пассивным способом имеет следующие недостатки:

– при боковом ветре не обеспечивается полет по ЛЗП и выход на РНТ с заданного направления;

– при отказе радиокомпаса или выключении радиостанции экипаж оказывается в затруднительном положении, т. к. ВС находится не на ЛЗП и курс следования на радиостанцию не подобран;

– в горной местности вследствие отклонения радиодромии от ЛЗП не обеспечивается безопасность полета.

В силу этих причин этот способ при полетах по воздушным трассам не применяют. Его можно использовать для вывода ВС на радиостанцию с небольших расстояний (30–50 км).

Полет на радиостанцию активным способомвыполняется следующим образом.

Курс ВС для полета на радиостанцию необходимо выдержать с учетом УС. При этом стрелку указателя радиокомпаса нужно удерживать на КУР = 360° + (±УС). Основное преимущество полета на радиостанцию активным способом перед пассивным и курсовым состоит в том, что при точном учете УС полет на радиостанцию выполняется по прямой и с постоянным курсом следования. Выход на радиостанцию обеспечивается с заданного направления. Полет на радиостанцию активным способом возможен:

– с выходом на ЛЗП;

– с выходом в КПМ (ППМ);

– с любого направления подбором курса следования.

Полет от радиостанции

Полет от радиостанции в заданном направлении может быть выполнен в том случае, если она расположена на ЛЗП и ИПМ, ППМ или контрольном ориентире. Полет от радиостанции может осуществляться с выходом на ЛЗП и с выходом в КПМ (ППМ). Пеленги, определяемые при полете от радиостанции, можно использовать для контроля пути по направлению.

Активный полет от радиостанции.Заключается в выдерживании курсового угла радиостанции с учетом угла сноса.

Чтобы ВС не сносило ветром с ЛЗП, продольную ось нужно отвернуть от ЛЗП в ту сторону, откуда дует ветер, на величину угла сноса.

КУР не может быть отрицательным, его отсчитывают в диапазоне от 0 до 360º. Поэтому КУР=360+УС. Например, если УС=-5, то необходимо выдерживать КУР=360+ (-5)=355.

При полете на радиостанцию формулой: КУР=360+УС

При полете от радиостанции используют формулу: КУР=180+УС.

Для использования данного способа не нужно даже знать курс, но, разумеется, необходимо знать УС.

31)Контроль пути по дальности пеленгованием боковой радиостанции и прокладкой ИПС на карте производится в следующем порядке:

1. Настроить радиокомпас на выбранную боковую радиостанцию.

2. Определить ИПС и заметить время пеленгования.

3. Проложить полученный ИПС на бортовой карте от выбранной радиостанции (рис. 10.11). Линия пеленга укажет, какого рубежа достигло ВС в момент пеленгования радиостанции.

Рис. 10.11. Контроль пути по боковой радиостанции

Этот простой способ обеспечивает достаточную точность контроля пути по дальности, его недостатком является необходимость прокладки пеленга на карте, что не всегда удобно.

Контроль пути по дальности выходом на предвычисленный КУР или МПР – наиболее распространенный способ, который, в отличие от предыдущего, не требует прокладки пеленга на карте.

Предвычисленным называется заранее рассчитанный КУР (МПР) для определения момента пролета КО, ПОД, ППМ или любой заданной точки, лежащей на ЛЗП. Выход на предвычисленный КУР или МПР осуществляется в следующем порядке;

1. При подготовке к полету:

– наметить на ЛЗП точки контроля и выбрать боковые радиостанции (рис. 10.12);

– для каждой намеченной точки измерить ИПР на выбранную радиостанцию и определить предвычисленный МПР по формуле

МПР_предв = ИПР – (± Δм);

– записать на карте у точек контроля рассчитанные значения МПР_предв.

Рис. 10.12. Расположение боковой радиостанции

2. В полете:

– рассчитать предвычисленный КУР по формуле

КУР_предв = МПР_предв – МК;

– за 3–5 мин до расчетного времени пролета точки контроля настроить радиокомпас на выбранную радиостанцию и следить за показаниями стрелки указателя радиокомпаса.

3. В момент, когда стрелка покажет

КУР = КУР_предв или МПР = МПР_предв,

ВС будет находиться над точкой контроля.

Если выдерживаемый МК при подлете к контрольной точке отличается от курса, взятого для расчета КУР_предв, то необходимо в КУР внести поправку, равную разности курсов. Когда фактический МК больше МК расчетного, КУР необходимо уменьшить на величину разности курсов и наоборот. Недостатком данного способа является то, что путь контролируется только в момент пролета намеченной точки.

Задачи, решаемые с помощью

Форма и размеры Земли

Поверхность, ограничивающая Землю как физическое тело, называется физической поверхностью Земли. Эта поверхность носит сложный нерегулярный характер, обусловленный неровностями рельефа: горами, равнинами, впадинами. На такой поверхности ввести какую-либо приемлемую для практики систему координат невозможно, поэтому эту поверхность необходимо «сгладить». Для этого используется понятие уровенной поверхности.

Уровенная поверхность – поверхность, во всех точках перпендикулярная направлению силы тяжести (отвесной линии).

В качестве сглаженной фигуры Земли разумно выбрать форму уровенной поверхности, совпадающей с физической поверхностью в морях и океанах, где нет неровностей рельефа. Такая фигура получила название геоида.

Геоид – фигура, образованная уровенной поверхностью, совпадающей в морях и океанах с их средней поверхностью.

В районах материков поверхность геоида проходит под уровнем рельефа местности. Эта поверхность называется средним уровнем моря, от которого отсчитывается высота рельефа и другие высоты. В России за начало уровня отсчета высот принято нулевое деление футштока (мерной линейки), установленной в Обводном канале г. Кронштадта.

Поверхность геоида хотя и является гладкой по сравнению с физической поверхностью Земли, но все же имеет неправильную форму (рис. 1.1). Геоид не имеет простого математического описания. Поэтому для упрощения вычислений расстояний и направлений его заменяют эллипсоидом вращения, который имеет правильную геометрическую форму и незначительно отличается от геоида.

Рис. 1.1. Поверхность геоида

Для удобства навигационных расчетов форму Земли представляют в виде шара с незначительным сжатием у полюсов. Этот эллипс имеет следующие размеры: экваториальный радиус а = 6378 км, полярный радиус b = 6357 км (рис. 1.2).

В воздушной навигации в большинстве случаях сжатием Земли пренебрегают и принимают Землю условно за шар, радиус которого составляет 6371 км.

Рис. 1.2. Земной элипсоид

Основные географические точки линии и круги на земном шаре.

Большим кругом называется окружность, образующаяся в результате сечения сферы плоскостью, проходящей через центр Земли.

Экватором называется большой круг, плоскость которого перпендикулярна оси вращения Земли (рис. 1.3).

Меридианом истинным, или географическим, называется большой круг, плоскость которого проходит через ось вращения Земли.

На земном шаре можно провести бесчисленное количество меридианов. Все меридианы сходятся у географических полюсов земли и расходятся к экватору (см. рис. 1.3).

Начальным меридианом, или нулевым, является Гринвичский меридиан, который когда-то проходил через расположенную вблизи г. Лондона Гринвичскую обсерваторию (сейчас обсерватория находится в другом месте, но меридиан сохранился).

Параллелью называется малый круг, плоскость которого перпендикулярна оси вращения и параллельна экватору (см. рис. 1.3).

Широтой (φ) (географической широтой) называется угол, заключенный между плоскостью экватора и направлением нормали к земной поверхности в данную точку (см. рис. 1.3). Нормалью называется перпендикуляр к касательной плоскости в данной точке эллипсоида.

Рис. 1.3. Сферические координаты

Широта отсчитывается от экватора к Северному и Южному полюсам от 0 до 90°. Если данная точка располагается в северном полушарии, то широта считается северной, а если в южном полушарии – южной. При расчетах по формулам северную широту можно считать положительной, а южную – отрицательной. На экваторе широта равна нулю, а на географических полюсах ±90°.

Долготой (λ) (географической долготой) называется двугранный угол, заключенный между плоскостями начального меридиана и меридиана данной точки (см. рис. 1.3).

Долгота отсчитывается в обе стороны от начального меридиана от 0 до 180°. Если данная точка расположена в восточном полушарии, то долгота считается восточной, если в западном полушарии – западной.

При расчетах по формулам западной и восточной долготе можно приписывать знаки соответственно «–» и «+» (или наоборот, как это принято, например, в США).

Единицами измерения широты и долготы являются угловые градусы, минуты и секунды, а иногда и их десятичные доли (десятые, сотые и т. д.). За рубежом используются следующие буквенные обозначения: N (North) – север; S (South) – юг; Е (East) – восток; W (West) – запад.

Одни и те же значения широты и долготы в документах аэронавига-ционной информации при выполнении различных навигационных расчетов могут быть представлены по-разному, например:

47° 23' 12" с.ш. = N47° 23.2' = +47.38667°.

124° 45' 45" з.д. = W124° 45.75' = –124.7625°.

Длина дуги большого круга (в частности, экватора и меридиана) протяженностью в 1° в среднем равна 111,2 км. Именно в среднем, потому что на самом деле меридиан является не окружностью, а эллипсом и длина дуги в 1° различна на разных широтах. Соответственно длина дуги в одну минуту составляет в среднем 1,853 км, а секунды – около 31 м.

Длина дуги параллели в 1° составляет 111,2 cosj.