Указания по выполнению контрольных работ

ФИЗИКА

МЕТОДИЧЕСКИЕ УКАЗАНИЯ И КОНТРОЛЬНЫЕ РАБОТЫ СТУДЕНТОВ ФАКУЛЬТЕТА НЕПРЕРЫВНОГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

Ижевск 2007

УДД 53 (078)

ББ 22. 3я 73

Р 89

Методические указания составлены на основе Государственного образовательного стандарта высшего профессионального образования по специальностям 1103302, 140106, 110301, 110303, 110304, утвержденного 17.03.2000 г.

Рассмотрены и рекомендованы к изданию кафедрой физики Ижевской ГСХА, протокол № 8 от « 23 » июня 2007 г.

Составитель: кандидат пед. наук, доцент кафедры физики И.Т. Русских

Р 89 Физика: Метод. указ./ Сост.: И.Т. Русских; – Ижевск: ИжГСХА, 2007.-

84 с.

В методических указаниях даны требования к оформлению контрольной работы по физике, представлены разъяснения по выполнению контрольной работы и решению задач, список рекомендуемой литературы.

Указания рассчитаны для студентов 1 курса факультета непрерывного профессионального образования заочного обучения.

УДК 53 (078)

ББК 22. 3я 73

© Ижевская ГСХА, 2007

Содержание стр.

1. Общие методические указания………………………………………….. 4

1.1. Самостоятельная работа с учебными пособиями ……………….. 4

1.2. Требования, предъявляемые к решению задач…………………… 5

1.3. Указания к выполнению контрольных работ……………………… 6

2. Механика и молекулярная физика

2.1.Основные законы и формулы механики и молекулярной

физики…………………………………........................................................ 9

2.2. Примеры решения задач…………………………………………… 15

3. Контрольная работа № 1…………………………………………………. 32

4. Основы электромагнетизма, оптики и физика вещества…………………. 39

4.1. Основные законы и формулы…………………………………... …. 39

4.2. Примеры решения задач………………………………………........ 44

5. Контрольная работа № 2…………………..……………………………… 60

6. Перечень примерных вопросов к экзаменам …………………………… 74

7. Приложения………………………………………………………………. 82

8. Список рекомендуемой литературы……………………………………. 83

1. ОБЩИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ

Учебная работа студента заочного отделения при изучении курса физики складывается из самостоятельной работы и очных занятий.

Самостоятельная работа включает в себя изучение курса по рекомендованным учебным пособиям, решение рекомендованных задач, выполнение контрольных работ.

Во время экзаменационной сессии студент слушает лекции, выполняет контрольные работы и сдает по ним зачет, а затем сдает экзамен.

Если при самостоятельной работе студенту встречаются трудности, то он может обратиться за консультацией на кафедру физики Ижевской государственной сельскохозяйственной академии. Консультация проводится в форме собеседования с преподавателем (если это возможно) или в письменном виде.

Самостоятельная работа с учебными пособиями

Самостоятельная работа с учебными пособиями является основным видом работы студента-заочника, и для успешного обучения необходимо принять следующие рекомендации:

1. Изучать курс физики необходимо систематически, в течение всего учебного года. Как показывает опыт работы со студентами-заочниками, попытка изучить курс физики в сжатые сроки, во время приезда на экзаменационную сессию, не приводит к положительным результатам. Поэтому необходимо в самом начале изучения курса, ознакомившись с программой, составить для себя график работы, т.е. распределить материал учебного пособия во времени по месяцам и работать с ним регулярно, стараясь жестко придерживаться графика.

2. Курс физики базируется на прочных знаниях школьного курса . Поэтому студенты, которые забыли те или иные разделы школьного курса, должны перед началом работы с вузовским учебным пособием повторить эти разделы по школьному учебнику. Это сократит затраты времени на изучение курса и позволит прочнее усвоить изучаемый материал.

3. Ни в коем случае нельзя изучать физику, только «читая» учебник. Как показывает педагогика, физические закономерности, особенно сопровождаемые математическими выкладками, при таком "чтении" не запоминаются, даже если все кажется ясным. Рекомендуется вести краткий конспект по каждому разделу изучаемого материала. В него следует записывать формулировки основных законов, математический вывод формул (обязательно!), наиболее важные чертежи, определения физических величин и единицы этих величин. В конспект следует также записывать те вопросы, которые остались невыясненными при самостоятельном изучении, чтобы быстро вспомнить их при встрече с преподавателем.

1. Следует учесть, что студент не должен ограничиваться лишь запоминанием физических формул. Те формулы, которые приводятся в учебном пособии с выводом, студент обязан уметь выводить. Для того, чтобы запомнить выводы формул, их необходимо два или три раза вывести самостоятельно, не заглядывая в учебник.

2. Рекомендуется обратить внимание на вопросы для самоконтроля, помещенные в конце каждого раздела пособия, так как аналогичные вопросы могут быть заданы студенту на зачете или на экзамене.

3. Все вычисления физических величин в настоящее время производятся, как правило, в международной системе единиц СИ, и лишь в некоторых случаях, когда это удобно, можно пользоваться внесистемными единицами. Соотношения между единицами СИ и внесистемными единицами приводятся в таблице, прилагаемой к контрольным заданиям. Необходимо запомнить, что без твердого знания единиц физических величин и без умения ими пользоваться, невозможно усвоить курс физики и тем более применять свои знания на практике и решать задачи.

Требования, предъявляемые к решению задач

Решение физических задач следует проводить в определенной последовательности, соблюдая ряд указанных ниже требований.

1. Выписать данные задачи в колонку в принятых стандартных буквенных обозначениях. Если необходимо обозначить несколько сходных величин, можно ввести большие и малые буквы или индексы (например, различные сопротивления можно обозначить как R₁, R₂, R₃, r и т. д.).

2. Величины, приведенные в условиях задачи, выразить в одной системе единиц, наиболее подходящей для данной задачи (предпочтительно в СИ).

3. Вспомнить физические законы, на основании которых следует производить решение задачи, дать формулировку этих законов, написать соответствующие им формулы.

4. Если это необходимо, то сделать схематический чертеж, рисунок, график, схему, поясняющие содержание задачи. Например, изобразить тело с приложенными к нему силами, график изменения объема газа при нагревании, схему электрической цепи, ход лучей в оптических системах и т.д.

5. Решение задачи сопровождать краткими пояснениями.

6. Решение большинства задач сводится к составлению уравнений, отражающих заданный физический процесс. Поэтому решение задачи необходимо осуществлять не в числовом, а в общем (буквенном) виде. При таком способе решения ответ получается в виде формулы, которая позволяет проверить полученный результат, а промежуточные выкладки дают возможность проверить любую часть решения задачи и исключить ошибки. Ответ, полученный в общем виде, позволяет сделать анализ решения, тогда как числовой ответ сделать это не дает возможности.

7. Получив ответ в виде расчётной формулы, следует проверить его на основании правил размерностей, т.е. убедиться, что размерности правой и левой частей равенства совпадают.

8. Проверив совпадение размерностей, следует провести анализ полученного ответа и выяснить, удовлетворяет ли он условиям задачи. Так, при решении квадратного уравнения получаются два ответа, один из которых может не удовлетворять данным задачи и его следует отбросить, обосновав это.

9. Сделав проверку, можно подставить в полученную формулу числовые значения величин, приведенных в условиях задачи. При арифметических подсчетах следует пользоваться правилами приближенных вычислений и производить расчеты лишь с тем количеством значащих цифр, которое определяется условиями задачи. Если правило размерностей было проверено, то подставлять наименования в расчетную формулу не следует, так как это лишь загромождает расчеты. В окончательном результате наименование полученной величины записывается в единицах СИ.

10. При решении следует пользоваться таблицами физических величин, которые приведены в приложениях к контрольным заданиям.

11. При выполнении контрольных работ рекомендуется пользоваться сводкой основных формул, приведенных в каждом разделе пособия.

Основные законы и формулы.

Скорость мгновенная v = 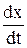или v = , где dх или dS – путь, проходимый точкой за время dt.

Ускорение мгновенное, тангенциальное а_τ = = ,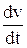

Нормальное ускорение a_n = v² /r, полное ускорение a = 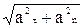, где r – радиус кривизны траектории.

Путь при равноускоренном движении тела .

Угловая скорость ω = 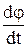, где dφ – угол поворота тела за время dt.

Угловое ускорение ε = . Уравнения равнопеременного вращательного движения ω = ω₀ + εt; φ = ω ₀t+ εt²/2, где ω₀ – начальная угловая скорость.

Связь между линейными угловыми величинами при движении точки

по окружности s = φr; v = ωr; a_τ = εr; a 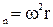; Т = 1/ν; ω = 2πν, где T – период, ν – частота вращения.

Импульс точки массы m, движущейся со скоростью v определяется р = mv,

Второй закон Ньютона для поступательного движения = m ,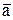

где 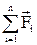– векторная сумма действующих на тело сил.

Закон сохранения импульса для изолированной системы .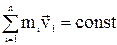

Сила трения скольжения f_тр = μF_n, где F_n— сила нормального давления, μ - коэффициент трения.

Скорости шаров массами m₁ и m₂ после центрального удара:

- абсолютно упругого: ; ;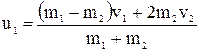

- абсолютного неупругого : 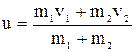, где v₁ и v₂ – скорости шаров массой m₁и m₂ до удара.

Работа переменной силы на пути 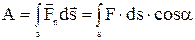, где α – угол между векторами 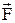и d . Мощность

Сила упругости: F = - kx, где k – коэффициент жесткости упругого элемента.

Потенциальная энергия упругодеформированного тела: W_П = kx²/2,

Сила гравитационного притяжения: F = Gm₁m₂/r², где G – гравитационная постоянная, r – расстояние между телами m₁ и m₂.

Потенциал гравитационного поля Земли: j = GM_З/(R₃ + h),

Напряженность гравитационного поля Земли: Е = GM_З/(R₃ + h)², где М_З – масса и R_з – радиус Земли, h – высота точки над поверхностью Земли.

Потенциальная энергия тела в поле земного тяготения вблизи поверхности: W_П = mgh, где g— ускорение свободного падения, h – высота тела

над поверхностью Земли.

Кинетическая энергия движущегося тела: Т = mv²/2 = р²/2m,

Закон сохранения механической энергии: W = Т +W_П = const.

Момент инерции материальной точки относительно оси: J = mR², где R - расстояние от точки массой m до оси вращения.

Моменты инерции некоторых тел массой m:

- сплошного однородного цилиндра (диска) относительно оси вращения

J = mR²/2;

- полого цилиндра относительно оси вращения J = mR²;

- шара относительно центра J = 0,4mR², где R - радиус цилиндра или шара;

- стержня длиной l, ось вращения которого перпендикулярна стержню

и проходит через его центр масс J₀ = ml²/12, стержня длиной l, ось вращения которого проходит через один из концов стержня J = ml²/3;

-тела c моментом инерции J₀ относительно произвольной оси вращения

(теорема Штейнера): J = J_o + md², где d – расстояние от оси вращения до центра масс тела.

Момент силы относительно оси вращения M = Fd, где d - плечо силы, т.е. кратчайшее расстояние от оси вращения до линии действия силы.

Основное уравнение динамики вращательного движения: M = ,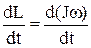

где L = Jω – момент импульса тела. То же, но при J = const M = J 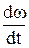= Jε,

Закон сохранения момента импульса: 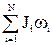= const.

Кинетическая энергия вращающегося тела: T = Jω²/2,

Работа при вращательном движении: dA = Mdφ,

Энергия покоя частицы массой m₀: E₀ = m₀c², где с – скорость света.

Зависимость от скорости v в релятивистской механике:

-импульса частицы: р = , длины тела: l = ,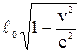

времени: t = 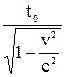, кинетической энергии: T = E – E₀ =m₀c² ,

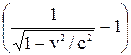- полной энергии частицы: E = mc² = ,

Теорема сложения скоростей в теории относительности: u^/ = ,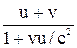

где u^/ - скорость тела в инерциальной системе К^/, которая движется со скоростью v относительно инерционной системы К, в которой тело движется со скоростью u.

Количество вещества: ν = , где N – число молекул, N_А – число Авогадро, m – масса вещества, μ – молярная масса. Уравнение Клапейрона – Менделеева: pV = RT, где р – давление газа, V – его объем, R –универсальная газовая постоянная, T – термодинамическая температура. Уравнение молекулярно – кинетической теории газов:

p = 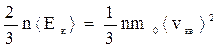, где n = N/V – концентрация молекул,

<E_к> - средняя кинетическая энергия поступательного движения молекул,

m₀ – масса, <υ_кв> - среднеквадратичная скорость молекулы.

Закон Дальтона для смеси газов: р = 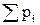, где p_i – парциальные давления компонентов смеси. Средняя кинетическая энергия молекул: <E_к> = ,

где i – число степеней свободы молекулы, k – постоянная Больцмана.

Внутренняя энергия идеального газа: U = .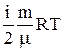

Скорости молекул: среднеквадратичная: <v_кв> = ,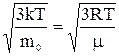

- среднеарифметическая: <v> = ,

- наиболее вероятная: v_в =

Средняя длина свободного пробега молекулы: <λ> = ,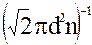

где d – эффективный диаметр молекулы.

Среднее число столкновений молекул в един. времени: <z> = .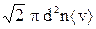

Уравнение диффузии: dm = -D 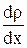dSdt, где – коэффициент диффузии, ρ – плотность, dS- элементарная площадка, перпендикулярная оси Х, 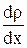- градиент плотности. Уравнение теплопроводности: dQ = - χ ,

где χ = c_v ρ 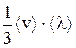– коэффициент теплопроводности, с_v – удельная теплоемкость при постоянном объёме, 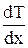- градиент температуры.

Сила внутреннего вязкого трения: , где – динамическая вязкость, - градиент скорости.

Удельная теплота плавления: r = 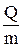. Удельная теплота парообразования: λ = 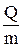. Удельная теплоемкость газа: С_уд = .

Молярная теплоемкость идеального газа: С= .

- изохорная: , изобарная: .

Уравнение первого начала термодинамики: dQ = dU + dA, где dU = C_vdT, dA = pdV.

Работа расширения газа при процессах:

- изобарный: ;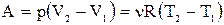

- изотермический: ;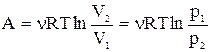

- адиабатический:

,

где 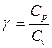= (i + 2)/i – показатель адиабаты или коэффициент Пуассона.

Уравнения адиабатического процесса:

; ; .

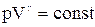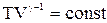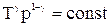Коэффициент полезного действия тепловой машины: η = .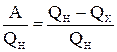

Коэффициент полезного действия цикла Карно: ,

где Q_Н и T_Н – количество теплоты, полученное от нагревателя, и его температура, Q_Х и T_Х – количество теплоты, переданное охладителю, и его температура.

Изменение энтропии при обратимом переходе системы из состояния 1 в состояние 2: .

Примеры решения задач

1. Движение тела массой 1кг задано уравнением: s = 6t³ + 3t + 2. Найти зависимость скорости и ускорения от времени. Вычислить силу, действующую на тело в конце второй секунды движения.

Дано: m=1 кг; s = 6t³ + 3t + 2; t = 2 с.

Найти: F, v, а.

Решение. Мгновенную скорость находим как производную от пути по времени: ; v = 18t² + 3 Мгновенное ускорение определяется первой производной от скорости по времени или второй производной от пути по времени: а = 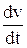= ; a = 36 t

Сила, действующая на тело, определяется по второму закону Ньютона: F = ma, где а,согласно условию задачи, есть ускорение в конце второй секунды. Тогда: F = m36t; F= 1∙ 36×2 = 72 кг∙м/с² =72 Н

Ответ: v = 18t² + 3; a = 36t; F = 72 H.

2. Стержень длиной 1 м движется мимо наблюдателя со скоростью

0,8 с. Какой покажется наблюдателю длина стержня?

Дано: l₀ = 1 м, v = 0,8 с.

Найти: l.

Решение. Зависимость длины тела от скорости в релятивистской механике выражается формулой: l = l₀ 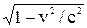, где l₀— длина покоящегося стержня; v— скорость его движения; с — скорость света в вакууме. Подставляя в формулу числовые значения, имеем: l =1∙ 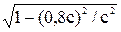= 1∙ = 0,6 м.

Ответ: l = 0,6 м.

3. Две частицы движутся навстречу друг другу со скоростями:

1) v = 0,5 с и u = 0,75 с;2) v = c и u = 0,75 с. Найти их относительные скорости в первом и во втором случаях.

Дано: 1) v = 0,5 с, u = 0,75 с; 2) v = c, и = 0,75 с. Найти: и^/_1, u^/₂.

Решение. Согласно теореме сложения скоростей в теории относительности:

;

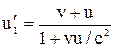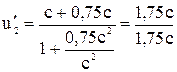где v, u — скорости соответственно первой и второй частиц; u' — их относительная скорость; с — скорость света в вакууме. Для первого и второго случаев находим: = 0,91 с; = с;

Это означает, во-первых, что ни в какой инерциальной системе отсчета скорость тела не может превзойти скорость света; во-вторых, скорость распространения света в вакууме одна и таже во всех инерциальных системах отсчёта.

Ответ: u¢₁ =0,91 с; u¢₂ = с.

4. На двух шнурах одинаковой длины, равной 0,8 м, подвешены два свинцовых шара массами 0,5 и 1 кг. Шары соприкасаются между собой. Шар меньшей массы отвели в сторону так, что шнур отклонился на угол a = 60°, и отпустили. На какую высоту поднимутся оба шара после столкновения? Удар считать центральным и неупругим. Определить энергию, израсходованную на деформацию шаров при ударе.

Дано: m₁ = 0,5 кг, m₂ =1 кг, a=60°; l = 0,8 м. Найти: h, DE_д.

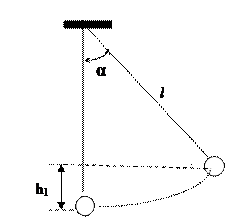Решение. Так как удар шаров неупругий, то после удара шары будут двигаться с общей скоростью v. Закон сохранения импульса при таком ударе имеет вид: m₁v₁ + m₂v₂ = (m₁ + m₂)v. (I)

1. Здесь v₁ и v₂ — скорости шаров до удара. Скорость большого шара до удара равна нулю (v₂ = 0). Скорость меньшего шара найдем, используя закон сохранения энергии. При отклонении меньшего шара на yгол a ему сообщается потенциальная энергия, которая при отпускании шара переходит в кинетическую энергию: m₁gh₁= m₁v²₁/2. Из рисунка видно, что высота h₁ равна: h₁= l(1— cos a) = 2l sin² (α/2);

Отсюда: 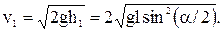(2)

Из уравнений (1) и (2) находим скорость шаров после удара:

v = m₁v₁/(m₁ + m₂) = 2m₁ 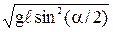(m₁ + m²) (3)

Кинетическая энергия, которой обладают шары после удара, переходит в потенциальную при последующем подъеме обоих шаров на высоту h:

(m₁ + m₂)v²/2 = (m₁ + m₂)gh,(4)

Из формулы (4) находим: h = v²/2g,или с учетом (3):

h == 2m²₁lsin²(α/2)/(m₁ + m₂)² h = 2∙0,5²∙0,8∙0,25/(0,5 +1)² = 0,044 м.

При неупругом ударе часть энергии шаров расходуется на их деформацию. Энергия деформации определяется как разность кинетических энергий шаров до и после удара: ΔЕ_Д =(m₁v²₁/2) – (m₁ + m₂)v²/2.

Используя уравнения (2) и (3), получаем: ΔЕ_Д = 2glm₁ 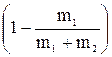sin²(α/2);

ΔЕ_Д =2·9,81м/с²·0,8м·0,5кг(1-0,5кг/1,5кг)·0,25=1,3 Дж.

Ответ: h = 0,044 м, ΔЕ_Д = 1,3 Дж.

5. Молот массой 70 кг падает с высоты 5 м и ударяет по железному изделию, лежащему на наковальне. Масса наковальни вместе c изделием 1330 кг. Считая удар абсолютно неупругим, определить энергию, расходуемую на деформацию изделия. Систему молот—изделие—наковальня считать замкнутой.

Дано: m 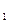= 70 кг, m₂ = 1330 кг, h = 5 м.

Найти: Е_Д.

Решение. По условию задачи система молот—изделие—наковальня считается замкнутой, а удар неупругий. На основании закона сохранения энергии можно считать, что энергия, затраченная на деформацию изделия, равна разности значений механической энергии системы до и после удара.

Считаем, что во время удара изменяется только кинетическая энергия тел, т.е. незначительным перемещением тел по вертикали во время удара пренебрегаем. Тогда для энергии деформации изделия имеем:

Е_Д = m₁v²/2 – (m₁ + m₂)v^{/ 2}/2, (1)

где v —скорость молота в конце падения с высоты h; v^/ —общая скорость всех тел системы после неупругого удара. Скорость молота в конце падения с высоты h определяется без учета сопротивления воздуха по формуле

v = ; (2) Общую скорость всех тел системы после неупругого удара найдем, применив закон сохранения количества движения: = const. (3)

Для рассматриваемой системы закон сохранения количества движения имеет вид: m₁v = (m₁ + m₂)v^/, откуда: v^/ = m₁v/(m₁ + m₂) (4)

Подставив в формулу (1) выражения (2) и (4), получим:

Е_Д = m₁m₂gh/(m₁ + m₂); Е_Д = 70∙9,8∙5∙1330/(1330 + 70) = 325,85 Дж

Ответ: Е_Д = 325,85 Дж.

6. Тело массой 1 кг под действием постоянной силы движется прямолинейно. Зависимость пути, пройденного телом, от времени задана уравнением: s = 2t² + 4t + 1. Определить работу силы за 10 с, с начала ее действия и зависимость кинетической энергии от времени.

Дано: m = 1 кг, s = 2t² + 4t + 1.

Найти: A, T = f(t).

Решение. Работа, совершаемая переменной силой, выражается через интеграл (1). Сила, действующая на тело, по второму закону Ньютона равна: F = ma или F = m (2). Мгновенное значение ускорения определяется первой производной от скорости по времени или второй производной от пути по времени. В соответствии с этим находим:

v = = 4t + 4 (3); a = = 4 м/с². (4)

Тогда F = m = 4m (5). Из выражения (3) определим ds: ds = (4t+4)dt. (6). Подставив (5) и (6) в уравнение (1), получим: A = .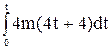

По этой формуле определим работу, совершаемую силой за время 10 с. с начала ее действия:

A = 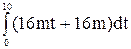= m 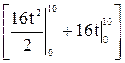= 1(8∙100 + 16∙10) = 960 Дж.

Кинетическая энергия определяется по формуле: T = mv²/2; (7)

Подставляя (3) в (7), имеем:

T = m(4t + 4)²/2 = m(16t² + 32t + 16)/2 = m(8t² + 16t +8)

Ответ:A = 960 Дж, T = m(8t² + 16t +8).

7. Протон движется со скоростью 0,7 с (с - скорость света). Найти

импульс и кинетическую энергию протона.

Дано: v = 0,7 с; с = 3∙10 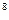м/с, m = 1,67∙10^-27 кг. Найти: р, Т.

Решение. Количество движения или импульс протона определяется по формуле: p= m₀v/ 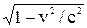= m₀v/ ; где m₀ —масса покоя протона; v— скорость движения протона; c — скорость света в вакууме; v/c = β — скорость протона, выраженная в долях скорости света.

p = 1,67∙10^-27∙3∙10⁸∙0,7/ = 4,91∙10^-19 кг·м/с.

В релятивистской механике кинетическая энергия частицы определяется как разность между полной энергией Еи энергией покояэтой частицы:

Т = Е – Е₀, где Е = m₀c²/ ; Е₀ = m₀c².

Подставив, имеем: Т = m₀c²(1/ - 1);

Вычисляем: T = 1,67∙10^-27∙(3∙10⁸)² (1/ - 1) = 0,6∙10^-10 Дж.

Ответ: р = 4,91∙10^-19 кг•м/с; Т = 0,6∙10^-10 Дж.

8. Какую наименьшую скорость нужно сообщить ракете, чтобы она, стартовав с Земли, не вернулась на Землю? Сопротивление атмосферы не учитывать.

Дано: R₃ = 6,37∙10⁶ м; g = 9,8 м/с²; R→∞.

Найти v .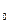

Решение. С удалением ракеты от Земли будет увеличиваться ее потенциальная энергия и уменьшаться кинетическая. По закону сохранения энергии:

mv₀²/2 – mv²/2 = m(GM/R_З – GM/R), (1)

где m- масса ракеты; М-масса Земли; G - гравитационная постоянная; v₀ и v- скорость ракеты относительно Земли в начальный и рассматриваемый моменты; R₃ и R- расстояния от центра Земли до ракеты в начальный и рассматриваемый моменты; GM/R- потенциал гравитационного поля Земли на расстоянии Rот ее центра. После преобразования уравнения (1) имеем:

v₀² - v² = 2GM(1/R_З - 1/R) ;

Ракета не вернется на Землю, если ее скорость vбудет больше или равна нулю на бесконечно большом расстоянии от Земли: v = 0 при R → ∞. Отсюда:

v₀² = 2GM/R_З; (2) Из закона всемирного тяготения следует, что на поверхности Земли GmM/R_З² = mg, откуда GM = gR_З² (3), где g -ускорение свободного падения на поверхности Земли. Подставляя формулу (2) в (3), находим:

v₀ = . Считая, что ракета приобретает нужную скоростьv_o уже вблизи поверхности Земли, находим: v₀ = = 11,2 км/с.

Такая скорость необходима для преодоления гравитационного поля Земли. Она называется второй космической или параболической скоростью.

Ответ: v_о = 11,2 км/с.

9. Тело брошено вверх с высоты 12 м под углом 30° к горизонту с начальной скоростью 12 м/с. Определить продолжительность полета тела до точек Аи В(cм. рисунок), максимальную высоту, на которую поднимается тело, и дальность полета тела. Сопротивление воздуха не учитывать.

Дано: H = 12 м, φ = 30°, v₀ = l2 м/с, g =9,8 м/с.

Найти: t_A, t_B, y_m, x_m.

Решение. В обозначенной на рис. системе координат проекции начальной скорости будут равны:v_ox = v₀cosφ (I), и v_0y = v₀sinφ (2).

Координаты тела с течением времени изменяются в соответствии с уравнением для равнопеременного движения:

y = H + v₀tsinφ – gt²/2 (3). x = v₀tcosφ (4).

Время подъема тела найдем из условия, что в наивысшей точке подъема скорость тела:

v_y = v₀sinφ – gt = 0 (2^/)

Тогда время подъема:

t_под = v₀sinφ/g (5).

Время спуска тела от точки С до точки А равно времени подъема, поэтому продолжительность полета тела от точки О 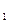, до точки Аравна:

t_A = 2t_под =2v₀sinφ/g. (6)

Максимальную высоту подъема найдем из уравнения (3), подставив в него время подъема из уравнения (5):

y_m = H + v₀²sinφ²/2g (7)

Время полета тела до точки Внайдем из уравнения (3), приравняв координату Y нулю (у = 0): t_B = v₀sinφ/g + (8)

Дальность полета найдем из уравнения (4), подставив в него время движения из уравнения (8): x_m = v₀t_Bcosφ (9) Тогда, решая совместно (6)-(9), получим:

t_A = 2∙12∙0,5/9,8 = 1,22 c. t_B = + = 2,29 c.

у_m = 12 + 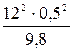= 13,8 м. x_m = 12∙2,29∙0,867 = 23,8 м.∙

Ответ: t_A = 1,22 c, t_B = 2,29 c, у_m= 13,8 м, x_m = 23,8 м.∙

10. По условию задачи 9 найти в момент приземления тела следующие величины: скорость и угол падения тела, тангенциальное и нормальное ускорения тела, радиус кривизны траектории в точке В.

Дано: H = 12 м, φ = 30°, v₀ = 12 м/с.

Найти: v_B, β, a_n, R.

Решение. Мгновенная, скорость в точке B(см. рис.):

v_B = 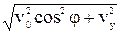Проекцию скорости v_у в точке Bнайдем из уравнения (2') задачи (9), подставив в него время

движения t_B. из (8):

v_y = v₀sinφ – gt_B = .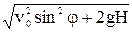

Результирующую скорость v в точке В найдем как:

v = =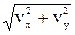

= =

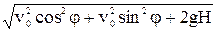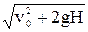= ; v = = 19,5 м/с.

Из рис. определим угол β, образуемый вектором скорости v c осью Оx:

sinβ = v_y/v = / ;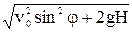

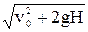sinβ = 0,85; β = arc sin 0,85 = 57₀40^/.

Построим в точке В «треугольник ускорений». Вектор тангенциального ускорения a_τ направлен вдоль вектора мгновенной скорости в данной точке, т. е. по касательной к траектории; вектор нормального ускорения а_n перпендикулярен вектору мгновенной скорости v. Из рис. видно, что

a_τ = g sinβ = gv_y/v; a_n = g cosβ = gv_x cosφ/ ;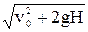

a_τ = 9,8∙0,85 = 8,3 м/с². a_n = 9,8∙12∙0,867/ = 5,25 м/с².

Радиус кривизны траектории в точке приземления (расстояние R = ОВ на рис.) определяем из уравнения: a_n = v²/R.

Отсюдаимеем: R = v²/a_n; R = 19,5²/5,25 = 72,5 м.

Ответ: v = 19,5 м/с, β = 57°40', а_τ = 8,3 м/с², a_n = 5,25 м/с², R = 72,5 м.

11.Тонкий стержень массой 300 г и длиной 50 см вращается с угловой скоростью 10 c в горизонтальной плоскости вокруг вертикальной оси, проходящей через середину стержня. Найти его угловую скорость, если в процессе вращения в той же плоскости стержень переместится так, что ось вращения пройдет через конец стержня.

Дано: m = 300 г = 0,3 кг, l = 50 см = 0,5 м, ω₁ = 10 c .

Найти: ω .

Решение. Воспользуемся законом сохранения момента импульса:

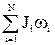= сonst, (1) где J - момент инерции стержня относительно оси вращения. Для изолированной системы тел векторная сумма момента импульсов остается постоянной. В данной задаче вследствие того, что распределение массы стержня относительно оси вращения изменяется, момент инерции стержня также изменится. В соответствии с (1) запишем:

J₁ω₁ = J₂ω₂ (2)

Известно, что момент инерции стержня относительно оси, проходящей через центр масс и перпендикулярной стержню, равен:

J₁ = J₀ = ml²/12. (3)

По теореме Штейнера: J = J₀ + md², где J - момент инерции тела относительно произвольной оси вращения; J₀ - момент инерции стержня относительно оси вращения, проходящей через центр масс; d- расстояние от центра масс до выбранной оси вращения. Найдем момент инерции относительно оси, проходящей через его конец и перпендикулярно стержню:

J₂ = J₁ + md²; J₂ = ml²/12 + m(l/2)² = ml²/3 (4)

Подставим формулы (3) и (4) в (2): ml²ω₁/12 = ml²ω₂/3,

откуда: ω₂ = ω₁/4; ω₂ = 10/4 = 2,5 c^-1.

Ответ:. ω₂ = 2,5 c^-1

12.Маховик массой 4 кг свободно вращается с частотой 720 мин^-1 вокруг горизонтальной оси, проходящей через его центр. Массу маховика можно считать равномерно распределенной по его ободу с радиусом 40 см. Через 30 с под действием тормозящего момента маховик остановился. Найти тормозящий момент и число оборотов, которое сделает маховик до полной остановки.

Дано: ω_t = 0, m = 4 кг, ν = 720 мин^{- 1}= 12с^-1; Δt = 30 с, R = 0,4 м.

Найти: М, N.

Решение. Для определения тормозящего момента М сил, действующих на тело, нужно применить основное уравнение динамики вращательного движения: JΔω = МΔt, (I), где J - момент инерции маховика относительно оси, проходящей через центр масс; Δω— изменение угловой скорости за промежуток времени Δt.

По условию задачи, Δω=-ω₀, где ω₀ — начальная угловая скорость, так как конечная углов