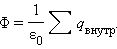Уравнение Клапейрона-Менделеева.

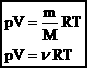
Где:

P-Давление

V-Молярный объем

R-Газовая постоянная (8,31 ^Дж⁄_{(моль∙К)}

T- Абсолютная температура (в кельвинах)

v- Количества вещества (которое можно расписать как m/M)

Формула устанавливает зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа.

38. Основное уравнение молекулярно-кинетической теории идеального газа.

Основное уравнение МКТ связывает микропараметры частиц ( массу молекулы, среднюю кинетическую энергию молекул, средний квадрат скорости молекул) с макропараметрами газа (р - давление, V - объем, Т - температура).

Давление газа на стенки сосуда пропорционально произведению концентрации молекул на среднюю кинетическую энергию поступательного движения молекулы.

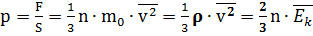
р - давление газа на стенки сосуда(Па)

n - концентрация молекул, т.е. число молекул в единице объема ( 1/м3) м0- масса молекулы (кг)

v^2 - средний квадрат скорости молекул ( м2/с2)

ρ - плотность газа (кг/м3)

Ek - средняя кинетическая энергия молекул (Дж)

Давление идеального газа на стенки сосуда зависит от концентрации молекул и пропорционально средней кинетической энергии молекул.

39Закон Максвелла для распределения молекул идеального газа по скоростям.

Распределение Ма́ксвелла — распределение вероятности, встречающееся в физике и химии. Оно лежит в основании кинетической теории газов, которая объясняет многие фундаментальные свойства газов, включая давление и диффузию.

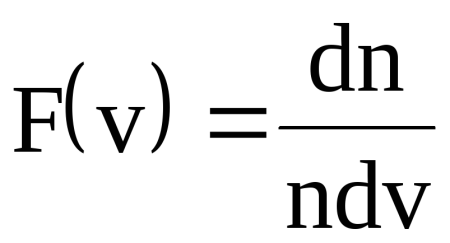
где n - общее число молекул в единице объема, т. е. концентрация; dn - число молекул в единице объема, скорости которых лежат в интервале от v до v+vd

40 . Барометрическая формула.

Барометрическая формула — зависимость давления или плотности газа от высоты в поле силы тяжести.

Где

p- давление

е- экспонента

Т- температура

x-высота

m- молярная масса

k (встречается также R, что даже вене)- Газовая постоянная

g- ускорение свободного падения

41. Среднее число столкновений и средняя длина свободного пробега молекул.

Молекулы газа, находясь в состоянии хаотического движения, непрерывно сталкиваются друг с другом. Введем определение средней длины свободного пробега молекул. Каждая, отдельно взятая молекула, между двумя последовательными соударениями проходит различные пути, но в среднем, в связи с огромным числом молекул, и их непрерывным хаотичным движением, можно говорит о средней длине свободного пробега молекул - <l>.

Минимальное расстояние, на которое сближаются при столкновении центры двух молекул, называется эффективным диаметром – d

Он зависит от скорости сталкивающихся молекул, т.е. от температуры газа (несколько уменьшается с ростом температуры).

Итак, за 1 секунду, молекула проходит в среднем путь, равный средней арифметической скорости <υ>, и если <z> - среднее число столкновений, испытываемых одной молекулой за 1 с, то среднюю длину свободного пробега можно рассчитать по формуле:

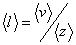42. Явления переноса (диффузия, теплопроводность), внутреннее трение.

Диф­фу­зия – это са­мо­про­из­воль­ное вза­им­ное про­ник­но­ве­ние мо­ле­кул од­но­го ве­ще­ства в про­ме­жут­ки между мо­ле­ку­ла­ми дру­го­го.

Теплопередача — это изменение внутренней энергии без совершения работы: энергия передается от более нагретых тел к менее нагретым.

Теплопередача бывает трех видов:

теплопроводность (непосредственный обмен энергией между хаотически движущимися частицами взаимодействующих тел или частей одного и того же тела);

конвекция (перенос энергии потоками жидкости или газа)

излучение (перенос энергии электромагнитными волнами).

Мерой переданной энергии при теплопередаче является количество теплоты ( ).

Вя́зкость (вну́треннее тре́ние) — одно из явлений переноса, свойство текучих тел (жидкостей и газов) оказывать сопротивление перемещению одной их части относительно другой. В результате работа, затрачиваемая на это перемещение, рассеивается в виде тепла.

43. Внутренняя энергия.

Внутренняя энергия — это величина, характеризующая собственное состояние тела, т.е. энергия хаотического (теплового) движения микрочастиц системы (молекул, атомов, ионов) и энергия взаимодействия этих частиц

Внутренняя энергия одноатомного идеального газа определяется по формуле

44. .

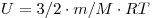Внутренняя энергия тела может изменяться только в результате его взаимодействия с другими телами. Существует два способа изменения внутренней энергии: теплопередача и совершение механической работы (например, нагревание при трении или при сжатии, охлаждение при расширении).

45. Число степеней свободы молекулы. Закон равномерного распределения энергии по степеням свободы.

Числом степеней свободы материального объекта называют число независимых координат, которые необходимо задать, чтобы однозначно определить положение этого объекта относительно рассматриваемой системы отсчета.

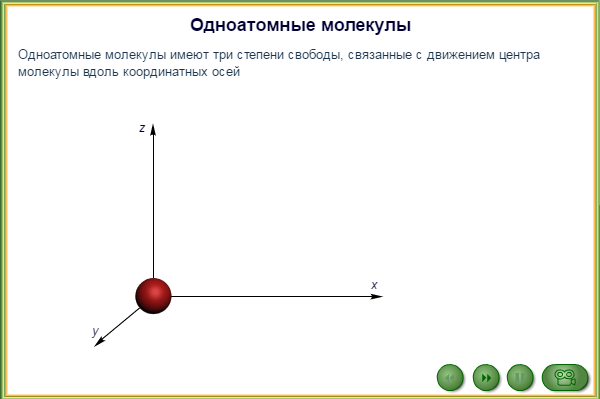Например, положение материальной точки в пространстве определяется тремя координатами x, y, z, следовательно, материальная точка обладает тремя степенями свободы

Tеорема о равномерном распределении энергии по степеням свободы:

Если система молекул находится в тепловом равновесии при температуре T, то средняя кинетическая энергия равномерно распределена между всеми степенями свободы и для каждой поступательной и вращательной степени свободы молекулы она равна:

kT/2.

Если рассматриваются и колебательные степени свободы, то для каждой колебательной степени свободы молекулы средняя кинетическая энергия равна kT, так как колебательное движение связано с наличием не только кинетической, но и потенциальной энергии, причем для малых (гармонических) колебаний среднее значение потенциальной энергии равно среднему значению кинетической. Поэтому на каждую колебательную степень свободы приходится:

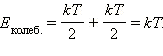46. Первое начало термодинамики.

Первый закон термодинамики, установленный на основании многочисленных опытов, утверждает, что изменение внутренней энергии ΔU системы равно сумме совершаемой над системой работы A' внешних сил и количества теплоты Q, переданного системе извне.

.

По сути дела, формулировка 1-го начала термодинамики послужила основанием для утверждения в физике понятия "энергия". С той поры оно заняло центральное место в физике, отодвинув на второй план введенное Ньютоном понятие "сила". Признание энергии как наиболее общего понятия, позволяющего рассматривать с единой точки зрения все явления и процессы, следует признать основным достижением науки XIX в.

47. Теплоемкость. Уравнение Майера.

Теплоёмкость тела характеризуется количеством теплоты, необходимой для нагревания этого тела на один градус:

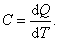(4.2.1)

Размерность теплоемкости: [C] = Дж/К.

Однако, теплоёмкость – величина неопределённая, поэтому пользуются понятиями удельной и молярной теплоёмкости.

Удельная теплоёмкость (С_уд) есть количество теплоты, необходимое для нагревания единицы массы вещества на 1 градус [C_уд] = Дж/К.

Для газов удобно пользоваться молярной теплоемкостью Cμ- количество теплоты, необходимое для нагревания 1 моля газа на 1 градус:

(4.2.2)

[Cμ] = Дж/(моль×К).

Из основного уравнения молекулярно-кинетической теории . При изобарическом процессе Р = const. Следовательно, из (4.2.7) получим:

.

(4.2.8)

Это уравнение Майера для одного моля газа.

Из этого следует, что физический смысл универсальной газовой постоянной в том, что R – численно равна работе, совершаемой одним молем газа при нагревании на один градус в изобарическом процессе.

Используя это соотношение, Роберт Майер в 1842 г. вычислил механический эквивалент теплоты: 1 кал = 4,19 Дж.

Полезно знать формулу Майера для удельных теплоёмкостей:

.

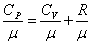или

.

48. Работа газа при изменении его объема.

Газ оказывает давление на любую стенку сосуда. Если стенка подвижна, то сила давления F совершит работу A, переместив поршень на расстояние DL.

Если DL невелико, то давление газа останется примерно постоянным. Тогда работа будет равна:

A = F·DL·cosa = P·S·DL,
где S - площадь поршня,
a - угол между направлением силы и перемещением поршня (a = 0).

Произведение S·DL равно изменению объема газа DV от начального V₁ до конечного V₂значения, т.е. S·DL =DV = V₁ - V₂. Тогда

A = P·(V₂ - V₁) = P·DV.

В изобарном процессе расширения газа P = const. Следовательно, при любом сколь угодно большом увеличении объема сила давления газа на поршень будет постоянной, и формула работы сохранит свой вид

A = P·(V₂ - V₁).

49. Применение первого начала термодинамики к изопроцессам (изохорный, изобарный, изотермический).

ПРИМЕНЕНИЕ 1 ЗАКОНА ТЕРМОДИНАМИКИ К ИЗОПРОЦЕССАМ.
Процесс	Постоянные	График	Изменение внутренней энергии	Запись 1-го закона термодинамики	Физический смысл
Изотермическое Расширение	m=const M=const T=const pV=const		U=const ΔU=0	Q=A'	Изотермический процесс не может происходить без теплопередачи. Все количество теплоты, переданное системе, расходуется на совершение этой системой механической работы.
Изотермическое Сжатие	m=const M=const T=const pV=const		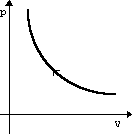U=const ΔU=0	A=-Q	Изотермический процесс не может происходить без теплопередачи. Вся работа внешних сил выделяется в виде тепла.
Изохорное Нагревание	m=const M=const V=const		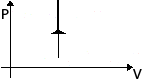p↑ T↑ U↑ ΔU>0	A=0 Q= ΔU	Все количество теплоты, переданное системе, расходуется на увеличение ее внутренней энергии.
Изохорное Охлаждение	m=const M=const V=const		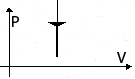p↓ T↓ U↓ ΔU<0	A=0 Q= ΔU<0	Система уменьшает свою внутреннюю энергию, отдавая тепло окружающим телам.
Изобарное расширение (нагревание)	m=const M=const p=const	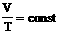	V­↑ T­↑ U­↑ ΔU>0	Q=ΔU+A' ΔU=Q-А'>0	Количество теплоты, переданное системе, превышает совершенную механическую работу. Часть тепла расходуется на совершение работы, а часть – на увеличение внутр. энергии.
Изобарное сжатие (охлаждение)	m=const M=const p=const	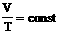	V↓ T↓ U↓ ΔU<0	ΔU=Q+A<0 Q<0	Количество теплоты, отдаваемое системой, превышает работу внешних сил. Часть тепла система отдает за счет уменьшениявнутр. энергии.
Адиабатное Расширение	m=const M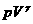=const =const		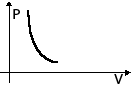ΔU<0 U↓ T↓	Q=0 A' > 0 ΔU=-A' < 0 A'=-ΔU	Система совершает механическую работу только за счет уменьшения своей внутренней энергии.
Адиабатное Сжатие	m=const M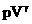=const =const		ΔU>0 U­↑ T­↑	Q=0 A>0 ΔU=A	Внутренняя энергия системы увеличивается за счет работы внешних сил.

50. Адиабатический процесс. Уравнение Пуассона. Работа при адиабатическом процессе.

Термодинамический процесс, в котором система при переходе из состояния 1 в состояние 2 не обменивается теплотой с окружающей средой, называют адиабатическим.

При возникновении ударной волны газ адиабатически сжимается и сильно нагревается, т.к. он не успевает отдать выделившуюся теплоту.

Метеориты при вхождении в атмосферу оплавляются и испаряются в основном по этой причине, а не из-за наличия трения и сопротивления при движении в атмосферном воздухе.

При адиабатическом процессе газ совершает работу за счет убыли его внутренней энергии.

Работу, совершаемую газом в адиабатическом процессе, найдем интегрируя выражение

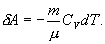
Полная работа

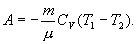
Уравнение Пуассона описывает адиабатный процесс, протекающий в идеальном газе.

Уравнение Пуассона имеет вид:

PV^k=const

Здесь V – объем, занимаемый газом, P– его давление, а k-величина называется показателем адиабаты.

Показатель адиабаты можно рассчитать, как отношение изобарной теплоемкости газа к его изохорной теплоемкости:

K= Cp/Cv

51. Давление Лапласа. Смачивание. Капиллярные явления

Наличие сил поверхностного натяжения и кривизны поверхности жидкости в капиллярной трубочке ответственно за дополнительное давление под искривленной поверхностью, называемое давлением Лапласа.

Pл=2G/r

G (сигма)- капиллярное давление

r- радиус кривизны

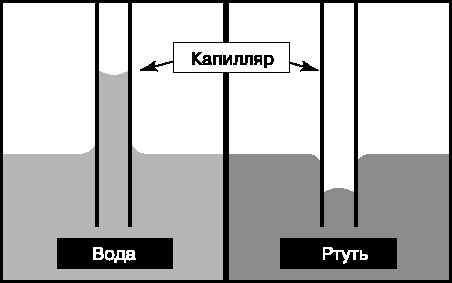
Смачивание и несмачивание- Если силы взаимодействия молекул жидкости с молекулами твердого тела больше сил взаимодействия между молекулами самой жидкости- жидкость смачивает поверхность.

Если меньше- не смачивает.

Капиллярные явления- изменение уровня жидкости в очень тонких трубках — капиллярах. Если диаметр капилляра мал, то мениски, образующиеся у его стен, сливаются друг с другом, образуя поверхность, близкую к сферической.

52. Закон Кулона. Точечный заряд. Диэлектрическая проницаемость среды.

Закон Кулона: сила взаимодействия двух точечных зарядов в вакууме прямо пропорциональна произведению модулей зарядов и обратно пропорциональна квадрату расстояния между ними.

Точечный заряд— идеализация, вводимая для упрощения описания поля заряженного тела или системы тел. Иногда также определяется как электрически заряженная материальная точка.

Диэлектрическая проницаемость среды (относительная) — физическая величина, характеризующая свойства изолирующей (диэлектрической) средыи показывающая, во сколько раз сила взаимодействия двух электрических зарядов в этой среде меньше, чем в вакууме

53. Напряженность электростатического поля.

Напряжённость электрического поля — векторная физическая величина, характеризующая электрическое поле в данной точке и численно равная отношению силы, действующей на неподвижный точечный заряд, помещённый в данную точку поля, к величине этого заряда

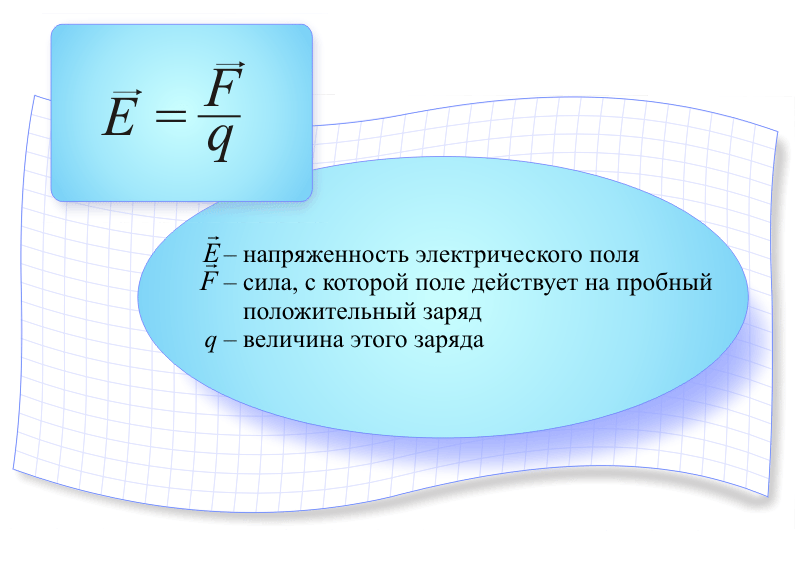
Из этого определения видно, почему напряжённость электрического поля иногда называется силовой характеристикой электрического поля

54. Поток вектора напряженности. Теорема Гаусса для электростатического поля в вакууме.

Полное число силовых линий, проходящих через поверхность S называетсяпотоком вектора напряженностиФ_Ечерез эту поверхность.

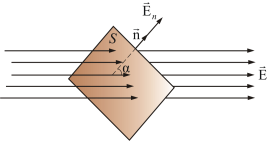
Теорема Гаусса утверждает:

Поток вектора напряженности электростатического поля 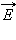через произвольную замкнутую поверхность равен алгебраической сумме зарядов, расположенных внутри этой поверхности, деленной на электрическую постоянную ε₀.

Для тупых как я: поток вектора напряженности зависит от заряда. В этом смысл теоремы Гаусса.

55. Потенциал электростатического поля.

Потенциал электростатического поля — скалярная величина, равная отношению потен­циальной энергии заряда в поле к этому заряду: 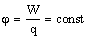Потенциал не зависит от величины заряда, помещенного в это поле.