Энтропия активации. Стерический фактор

Кроме энергии активации важным условием осуществления химической реакции является ориентация молекул в момент столкновения. Большую роль играют размеры и форма молекул, место расположения реакционно-способных атомов или групп атомов в молекуле.

Вероятность необходимой для взаимодействия ориентации молекул при столкновении

,

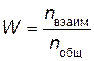где, n_взаим - число способов ориентации, приводящих к взаимодействию; n_общ - общее число возможных способов ориентации.

Энтропия активации (в расчете на 1 моль) по уравнению Больцмана

.

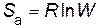Вероятность необходимой ориентации

.

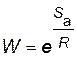Чем больше вероятность необходимой для реакции ориентации, т.е. чем больше значение энтропии активации и чем меньше значение энергии активации, тем выше скорость реакции и, соответственно, константа скорости

,

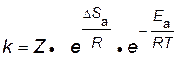(2.15)

где Z – коэффициент пропорциональности.

Для бимолекулярных реакций Z – это число столкновений частиц в единице объема за единицу времени (1с, 1 см³).

Уравнение (2.15) называют основным уравнением химической кинетики. Энергия активации и энтропия активации являются теми факторами, посредством которых сказывается влияние природы реагирующих веществ на скорость реакции.

Множитель 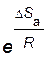называется стерическим фактором (или стерическим множителем, или фактором вероятности).

Стерический фактор 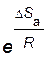и частота столкновений Z учитываются в уравнении Аррениуса (2.14) через предэкспоненциальный множитель А.

Применение уравнения Аррениуса

Энергию активации можно рассчитать по экспериментальным данным графическим или аналитическим способами, используя уравнение Аррениуса

,

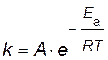представив его в логарифмическом виде

.

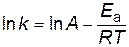(2.16)

Графический способ

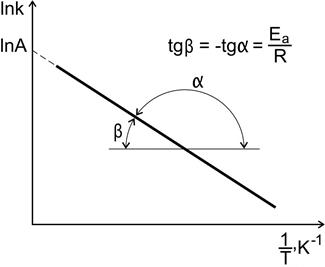
Рис. 8. Зависимость константы скорости реакции от температуры

По экспериментальным значениям константы скорости реакции при различных температурах строят график зависимости lnk = f ( 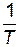) (рис. 8).

По тангенсу угла наклона прямой к оси абсцисс вычисляют энергию активации

.

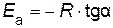Аналитический способ

Если предположить, что для выбранной реакции величины А и Е_а постоянны в небольших пределах температур от Т₁ до Т₂, то уравнение Аррениуса (2.16) можно применить для двух различных температур (Т₂> Т₁; k (Т₂) = k₂; k (Т₁) = k₁)

;

.

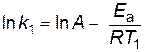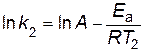В результате вычитания первого уравнения из второго получим

,

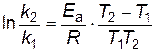(2.17)

следовательно,

.

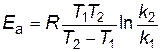(2.18)

Под символом логарифма находится отношение констант скоростей реакции при двух температурах, поэтому константы можно заменить любыми пропорциональными им величинами при тех же температурах. Например, вместо констант скоростей можно подставить скорости реакции, если исходные концентрации реагирующих веществ при измерении скоростей в обоих опытах были одинаковы и скорость изменилась только под влиянием изменения температуры. Тогда получим следующие выражения:

;

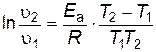(2.19)

.

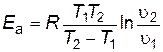(2.20)

Каталитические реакции

Основные понятия

Катализаторы - вещества, изменяющие скорость реакции и остающиеся к концу реакции химически неизменными.

Явление изменения скорости реакции под действием таких веществ называется катализом.

Реакции, протекающие под действием катализаторов, называются каталитическими реакциями.

Реакции, в которых катализатором является продукт реакции, называются автокаталитическими.

Важным свойством катализаторов является селективность (избирательность) их действия, проявляющаяся в увеличении скорости только определенной из нескольких возможных реакций.

Вещества, малые примеси которых могут сильно снижать или полностью подавлять активность катализатора, называются каталитическими ядами.

Промоторы – вещества, которые увеличивают активность катализаторов, хотя сами таковыми не являются.

По фазовому принципу различают гомогенный и гетерогенный катализ.