Свойства неопределённого интеграла
Цели
Знать:
v Определения первообразной и неопределённого интеграла; их геометрический смысл;
v свойства неопределённого интеграла;
v таблицу интегралов от основных элементарных функций;
v основные методы интегрирования.
Уметь:
v Находить интегралы методом непосредственного интегрирования.
▼Функция F(x), определённая в промежутке (a;b), называется первообразной функции f(x)в этом промежутке, если для любого значения 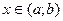 выполняется равенство
выполняется равенство

 или dF(x)=f(x)dx (1) ▲
или dF(x)=f(x)dx (1) ▲
Пример.1) Функция F(x)=х5 — первообразная функции f(x)=5х4 в промежутке  , поскольку
, поскольку 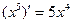 для всех х;
для всех х;
2) функция F(x)=lnx первообразная функции 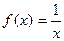 в промежутке
в промежутке  , так как
, так как  ;
;
3) функция F(x)=arcсosx — первообразная функции 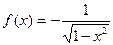 в интервале (-1;1), т.к.
в интервале (-1;1), т.к.  .
.
Теорема. Если F(x) — первообразная функции f(x) на промежутке (a;b),то множество всех первообразных для f(x) задаётся
Ф(х)=F(x)+С, (2)
где С — произвольная постоянная.
▼Совокупность всех первообразных для функции f(x) на промежутке (a;b) называется неопределённым интегралом от функции f(x) и обозначается  ,
,
где 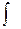 — знак неопределённого интеграла,
— знак неопределённого интеграла,
функция f(x) — подынтегральная функция,
выражение f(x)dx — подынтегральное выражение.
Таким образом,

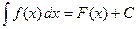 , (3)
, (3)
где F(x) — некоторая первообразная для f(x), С — произвольная постоянная.
Аудиторное занятие
Пользуясь основными правилами и формулами интегрирования, найти следующие интегралы, результаты проверить дифференцированием:
aЗдесь и далее при записи ответов постоянную С мы фиксировать не будем.
№1.  . Ответ: 3х.
. Ответ: 3х.
№2. 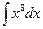 . Ответ:
. Ответ:  .
.
№3.  . Ответ:
. Ответ:  .
.
№4.  . Ответ: tgx-3 cosx.
. Ответ: tgx-3 cosx.
№5.  . Ответ:
. Ответ:  .
.
№6.  . Ответ:
. Ответ: 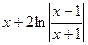 .
.
№7.  . Ответ:
. Ответ: 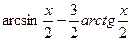 .
.
№8.  . Ответ:
. Ответ:  .
.
№9.  . Ответ:
. Ответ: 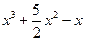 .
.
№10.  .
.
Ответ:  .
.
№11. 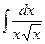 . Ответ:
. Ответ:  .
.
№12. 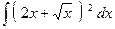 . Ответ:
. Ответ: 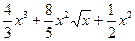 .
.
№13.  . Ответ:
. Ответ:  .
.
№14.  .
.
Указание. Применить формулу  .
.
Ответ: -x-ctgx.
№15. 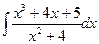 . Ответ:
. Ответ:  .
.
№16.  .
.
Указание. Применить формулу cos2x=cos2x-sin2x.
Ответ: -tgx-ctgx.
№17.  .
.
Ответ:  .
.
№18.  .
.
Указание. Применить формулу  .
.
Ответ:  .
.
№19.  . Ответ:
. Ответ:  .
.
№20. 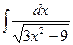 . Ответ:
. Ответ:  .
.
№21.  . Ответ:
. Ответ:  .
.
№22.  . Ответ: -2cos x.
. Ответ: -2cos x.
№23.  . Ответ:
. Ответ:  .
.
Домашнее задание
Пользуясь основными правилами и формулами интегрирования, найти следующие интегралы, результаты проверить дифференцированием:
№24.  . Ответ:
. Ответ:  .
.
№25.  . Ответ:
. Ответ:  .
.
№26. 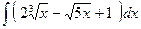 . Ответ:
. Ответ:  .
.
№27.  . Ответ:
. Ответ:  .
.
№28.  . Ответ:
. Ответ:  .
.
№29.  . Ответ:
. Ответ:  .
.
№30. 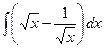 . Ответ:
. Ответ:  .
.
№31. 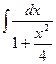 . Ответ:
. Ответ: 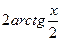 .
.
№32. 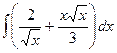 . Ответ:
. Ответ: 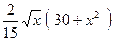 .
.
№33.  . Ответ: x+cos x.
. Ответ: x+cos x.
№34. 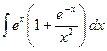 . Ответ:
. Ответ: 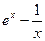 .
.
№35.  . Ответ:
. Ответ:  .
.
№36.  . Ответ:
. Ответ: 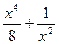 .
.
№37.  .
.
Указание. Учесть, что 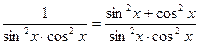 .
.
Ответ: tg x - ctg x.
№38.  . Ответ: cos x-3ctg x.
. Ответ: cos x-3ctg x.
№39. 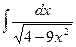 . Ответ:
. Ответ:  .
.
№40. 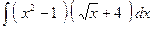 .
.
Ответ: 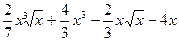 .
.
№41.  . Ответ:
. Ответ:  .
.
№42.  . Ответ:
. Ответ:  .
.
№43.  . Ответ:
. Ответ: 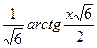 .
.
№44.  . Ответ: x-arctg x.
. Ответ: x-arctg x.
№45.  . Ответ:
. Ответ:  .
.
Дополнительные задания
Пользуясь основными правилами и формулами интегрирования, найти следующие интегралы, результаты проверить дифференцированием:
№46.  . Ответ:
. Ответ:  .
.
№47. 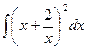 . Ответ:
. Ответ: 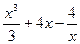 .
.
№48.  . Ответ:
. Ответ:  .
.
№49.  . Ответ: -4cos x+2x4-11tg x.
. Ответ: -4cos x+2x4-11tg x.
№50.  . Ответ:
. Ответ:  .
.
№51. 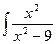 . Ответ:
. Ответ:  .
.
№52. 
Ответ: 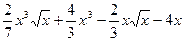 .
.
№53.  . Ответ:
. Ответ: 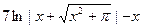 .
.
№54.  . Ответ:
. Ответ:  .
.
№55.  . Ответ:
. Ответ: 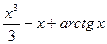 .
.
№56. 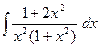 . Ответ:
. Ответ:  .
.
№57.  . Ответ:
. Ответ:  .
.
№58.  , где a,b — const.
, где a,b — const.
Ответ:  .
.
№59.  , где a,b — const.
, где a,b — const.
Ответ: 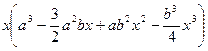 .
.
№60.  .
.
Указание. Учесть, что  .
.
Ответ:  .
.
№61.  .
.
Указание. Учесть, что  .
.
Ответ:  .
.
№62. 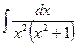 .
.
Указание. Учесть, что  .
.
Ответ:  .
.
№63. 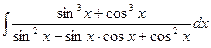 .
.
Указание. Воспользоваться формулой суммы кубов.
Ответ: sin x-cos x.
Занятие 2
Метод подстановки (замена переменной)
Цели
Знать:
v таблицу дифференциалов от основных элементарных функций;
v таблицу интегралов от основных элементарных функций;
v основные приёмы метода подведения под дифференциал.
Уметь:
v Находить интегралы методом непосредственного интегрирования и методом подведения под дифференциал.
Если интеграл непосредственно не берётся, то во многих случаях метод интегрирования заменой переменной приводит к цели.
Пусть требуется найти 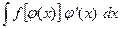 , где подынтегральная функция непрерывна. Применив подстановку
, где подынтегральная функция непрерывна. Применив подстановку  , получим
, получим

 . (9)
. (9)
Не существует общего «рецепта», следуя которому можно всегда понять, какую подстановку надо применить к данному интегралу, однако после приобретённого навыка вы скоро научитесь этому. Однако следует иметь в виду следующие полезные подсказки:
- Если под знаком интеграла стоит сложная функция
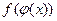 , как правило, используется подстановка
, как правило, используется подстановка  .
. - Если в подынтегральном выражении есть готовый дифференциал функции
 , т.е. выражение
, т.е. выражение  , то имеет смысл попробовать подстановку
, то имеет смысл попробовать подстановку  . Поэтому целесообразно запомнить таблицу дифференциалов.
. Поэтому целесообразно запомнить таблицу дифференциалов.
- Правило поправочного коэффициента

 , (a, b — const). (10)
, (a, b — const). (10)
Постановка задачи. Найти 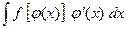 .
.
План решения. Для нахождения интеграла следует:
- переписать интеграл в виде
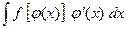 ;
; - заменить
 , что приводит к равенству
, что приводит к равенству  ;
; - вычислить последний интеграл;
- в полученном ответе произвести обратную замену t=
 .
.
№2.Найти интегралы:1)  ; 2)
; 2) 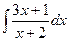 ;
;
3)  ; 4)
; 4)  ; 5)
; 5)  ;
;
6)  , 7)
, 7) 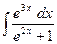 .
.
►1)  =
= 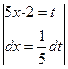 =
= 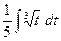 =
=  =
=  =
=
= 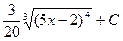 ;
;
Здесь и далее при записи решений примеров все промежуточные выкладки мы будем заключать между вертикальными линиями.
2) 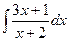 =
=  =
=  =
=
=  =3х-ln|x+2|+C;
=3х-ln|x+2|+C;
Замечание. Фактически мы здесь разделили числитель на знаменатель, т.е. из неправильной алгебраической дроби выделили целую часть.
Проверка. 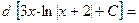
 ;
;
3)  =
=  =
= 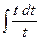 =
=  =t+C=
=t+C=  ;
;
4)  =
=  =
= 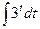 =
=  =
=  ;
;
5)  =
= 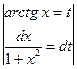 =
= 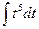 =
=  =
=  ;
;
6)  =
= 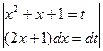 =
=  =lnt+C=ln|x2+x+1|+C;
=lnt+C=ln|x2+x+1|+C;
7) 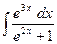 =
= 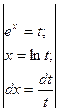 =
=  =
=  =
=  =
=
=  = t-arctg t=
= t-arctg t= 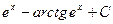 .◄
.◄
Аудиторное занятие
Найти интегралы:
№64. 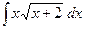 . Ответ:
. Ответ: 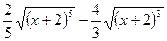 .
.
№65.  . Ответ:
. Ответ:  .
.
№66.  . Ответ:
. Ответ: 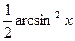 .
.
№67.  . Ответ:
. Ответ:  .
.
№68.  . Ответ:
. Ответ:  .
.
№69.  . Ответ:
. Ответ:  .
.
№70.  . Ответ:
. Ответ:  .
.
№71.  . Ответ:
. Ответ:  .
.
№72. 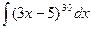 . Ответ:
. Ответ:  .
.
№73.  . Ответ: ln|x2+5x-6|.
. Ответ: ln|x2+5x-6|.
№74.  . Ответ:
. Ответ:  .
.
№75.  . Ответ:
. Ответ:  .
.
№76.  . Ответ: sin(ln x).
. Ответ: sin(ln x).
№77.  . Ответ:
. Ответ: 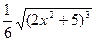 .
.
№78.  . Ответ:
. Ответ:  .
.
№79. 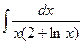 . Ответ: ln|2+ln x|.
. Ответ: ln|2+ln x|.
№80.  .
.
Указание. Подстановка х3=t. Ответ:  .
.
№81.  . Ответ:
. Ответ:  .
.
№82.  . Ответ:
. Ответ:  .
.
№83.  . Ответ: x-ln|ex+1|.
. Ответ: x-ln|ex+1|.
Домашнее задание
Найти интегралы:
№84.  . Ответ:
. Ответ:  .
.
№85. 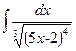 . Ответ:
. Ответ:  .
.
№86.  . Ответ:
. Ответ:  .
.
№87. 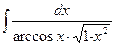 . Ответ: -ln |arccos x|.
. Ответ: -ln |arccos x|.
№88.  . Ответ:
. Ответ:  .
.
№89.  . Ответ:
. Ответ:  .
.
№90.  . Ответ:
. Ответ:  .
.
№91.  . Ответ:
. Ответ: 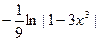 .
.
№92.  . Ответ:
. Ответ:  .
.
№93. 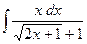 . Ответ:
. Ответ:  .
.
№94.  . Ответ:
. Ответ:  .
.
№95.  . Ответ:
. Ответ:  .
.
№96.  . Ответ:
. Ответ:  .
.
№97.  .
.
Указание. Выделить 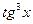 . Ответ:
. Ответ:  .
.
№98.  . Ответ:
. Ответ:  .
.
№ 99. 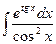 . Ответ:
. Ответ:  .
.
№100.  . Ответ:
. Ответ:  .
.
№101.  .
.
Указание.  . Ответ:
. Ответ:  .
.
№102.  . Ответ:
. Ответ:  .
.
№103.  . Ответ:
. Ответ:  .
.
№104.  . Ответ:
. Ответ:  .
.
Дополнительные задания
Найти интегралы:
№105. 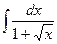 . Ответ:
. Ответ:  .
.
№106. 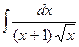 . Ответ:
. Ответ: 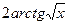 .
.
№107.  . Ответ:
. Ответ: 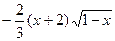 .
.
№108.  . Ответ: x-5ln|x+3|.
. Ответ: x-5ln|x+3|.
№109.  . Ответ:
. Ответ:  .
.
№110.  . Ответ:
. Ответ: 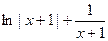 .
.
№111.  . Ответ:
. Ответ:  .
.
№112.  . Ответ:
. Ответ:  .
.
№113.  . Ответ:
. Ответ:  .
.
№114.  . Ответ:
. Ответ: 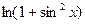 .
.
№115.  . Ответ:
. Ответ:  .
.
№116. 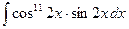 . Ответ:
. Ответ: 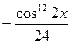 .
.
№117. 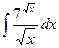 . Ответ:
. Ответ: 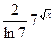 .
.
№118.  . Ответ:
. Ответ: 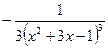 .
.
№119. 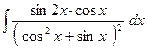 . Ответ:
. Ответ: 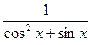 .
.
№120.  . Ответ:
. Ответ:  .
.
№121.  . Ответ:
. Ответ: 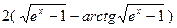 .
.
№122.  . Ответ:
. Ответ:  .
.
№123.  . Ответ:
. Ответ:  .
.
№124. 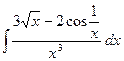 . Ответ:
. Ответ: 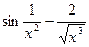 .
.
№125.  . Ответ:
. Ответ: 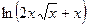 .
.
№126. 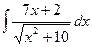 . Ответ:
. Ответ:  .
.
№127.  . Ответ:
. Ответ: 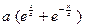 .
.
№128.  . Ответ:
. Ответ:  .
.
№129. 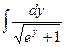 . Ответ:
. Ответ: 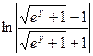 .
.
№130.  . Ответ:
. Ответ:  .
.
№131.  . Ответ:
. Ответ:  .
.
№132. 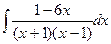 . Ответ:
. Ответ:  .
.
№133.  .
.
Ответ:  .
.
№134.  .
.
Ответ: 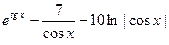 .
.
№135. 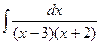 .
.
Указание. Учесть, что 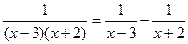 .
.
Ответ:  .
.
Примерный вариан решения
индивидуального задания
Найти неопределённые интегралы:
№1.  .
.
► 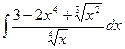 =
=  =
=
=  =
=
=  .◄
.◄
№2.  .
.
►  =
=  =
=  .◄
.◄
№3.  .
.
►  =
=  .◄
.◄
№4. 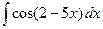 .
.
► 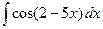 =
=  .◄
.◄
№5.  .
.
►  =
=  =
=  =
=
=  .◄
.◄
№6. 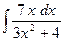 .
.
► 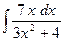 =
=  =
= 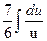 =
=  =
=
=  .◄
.◄
№7.  .
.
►  =
=  =
=  .◄
.◄
№8.  .
.
►  =
=  .◄
.◄
№9.  .
.
►  =
= 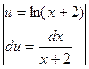 =
=  =
= 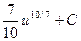 =
=
=  .◄
.◄
№10.  .
.
►  =
= 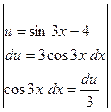 =
=  =
=
=  =
= 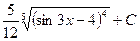 .◄
.◄
№11.  .
.
►  =
= 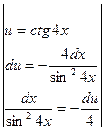 =
=  =
=
= 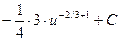 =
=  .◄
.◄
№12.  .
.
►  =
=  =
=  =
=
=  =
=  =
= 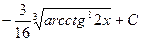 .◄
.◄
№13.  .
.
►  =
=  =
=  =
=  =
=
=  .◄
.◄
№14.  .
.
►  =
= 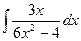 +
+  =
= 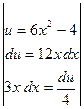 =
=
=  =
= 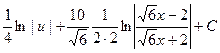 =
=
=  .◄
.◄
№15.  .
.
►  =
=  -
-  =
=  =
=
= 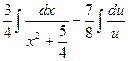 =
=  =
=
= 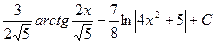 .◄
.◄
№16.  .
.
►  =
=  =
=  =
=  =
=
=  .◄
.◄
Занятие 3
Интегрирование по частям
Цели
Знать:
v Суть метода интегрирования по частям;
v основные типы интегралов, которые удобно вычислять методом интегрирования по частям;
Уметь:
v Применять метод интегрирования по частям при нахождении интегралов.
Пусть u и v — две функции аргумента х, имеющие производные  и
и  . Тогда справедлива формула:
. Тогда справедлива формула:

 . (11)
. (11)
При нахождении интегралов методом интегрирования по частям удобно пользоваться таблицей 1 выбора функции u=u(x).
Таблица 1
Таблица выбора функции u=u(x)
| вид интеграла | u |
 ; ; 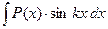 ; ;  . . | u=P(x) |
 ; ;  ; ;  ; ; 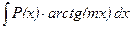 ; ;  . . | u= 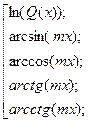 |
возвратные  ; ;  ; ;  . . | u=  или u= или u=  . . 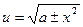 . . |
Постановка задачи.Найти неопределённый интеграл  .
.
План решения.Пусть v(x) имеет очевидную первообразную V(x), а u(x) — дифференцируемая функция, причём её производная является более простой функцией, чем u(x).
- Выбрать u(x), dv, используя таблицу выбора функции u(x);
- Найти du; v;
- Применить формулу (11).
· В некоторых случаях для сведения данного интеграла к одной из формул простейших интегралов формула (11) применяется несколько раз.
- Иногда искомый интеграл определяется из алгебраического уравнения, получающегося с помощью интегрирования по частям (возвратные интегралы);
- Записать ответ.
№3. Найти интегралы: 1)  ; 2)
; 2) 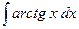 ;
;
3)  ; 4)
; 4)  .
.
►1)  =
=  =
=  =
=
=  ;
;
2) 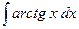 =
=  =
=
=  =
= 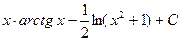 ;
;
3)  =
=  =
=
= 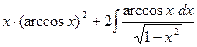 .
.
Этот интеграл также находим методом интегрирования по частям
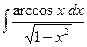 =
= 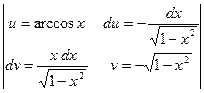 =
=
= 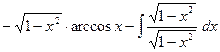 =
=  .
.
Следовательно,
 =
=  ;
;
4)  =
= 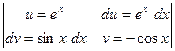 =
=
= 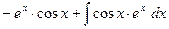 .
.
Этот интеграл также находим методом интегрирования по частям:

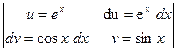 =
=
=  .
.
Подставив это выражение в последнее равенство, имеем:

по условию это выражение равно  , т.е.
, т.е.
 =
=  .
.
Разрешим данное выражение относительно интеграла (как неизвестного):
 , следовательно,
, следовательно,
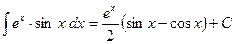 .◄
.◄
Аудиторное занятие
Найти интегралы:
№136.  . Ответ: sin x-x cos x.
. Ответ: sin x-x cos x.
№137. 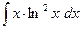 . Ответ:
. Ответ: 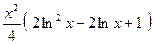 .
.
№138.  . Ответ:
. Ответ:  .
.
№139.  . Ответ:
. Ответ:  .
.
№140. 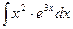 . Ответ:
. Ответ:  .
.
№141.  . Ответ:
. Ответ:  .
.
№142.  . Ответ: xtg x+ln|cos x|.
. Ответ: xtg x+ln|cos x|.
№143.  . Ответ:
. Ответ:  .
.
№144.  .
.
Указание. Подстановка t=ln x.
Ответ:  .
.
№145. 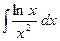 . Ответ:
. Ответ:  .
.
№146.  . Ответ:
. Ответ:  .
.
№147.  .
.
Ответ:  .
.
Домашнее задание
Найти интегралы:
№148. 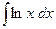 . Ответ: x(ln x-1).
. Ответ: x(ln x-1).
№149.  . Ответ:
. Ответ:
