А. Интегрирование линейного однородного уравнения
Рассмотрим линейное однородное уравнение 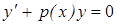 (2)
(2)
Это уравнение с разделяющимися переменными. Пусть 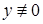 , тогда
, тогда 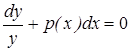 . (3)
. (3)
Отсюда общий интеграл 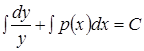 или
или 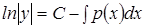
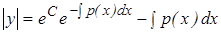
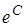 заменяем на
заменяем на 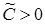
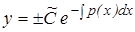
Но 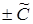 есть любое число, кроме нуля. Положим
есть любое число, кроме нуля. Положим 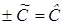 .
.
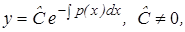
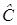 – произвольная постоянная (4). Это общее решение не содержит функции
– произвольная постоянная (4). Это общее решение не содержит функции 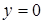 , которая является решением уравнения (2). Для того чтобы общее решение содержало бы все решения, его надо записать в виде:
, которая является решением уравнения (2). Для того чтобы общее решение содержало бы все решения, его надо записать в виде: 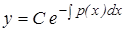 (5),
(5),
где С – произвольная постоянная, принимающая любые значения.
Пример. Написать общее решение уравнения 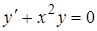 .
.
Решение. Имеем 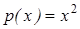 . Поэтому
. Поэтому 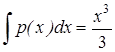 (произвольную постоянную можно считать = 0). И
(произвольную постоянную можно считать = 0). И 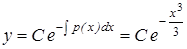 – общее решение.
– общее решение.
В. Интегрирование линейного неоднородного уравнения
Рассмотрим линейное неоднородное уравнение 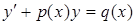 (1)
(1)
Для его интегрирования применим метод вариации произвольной постоянной. Положим 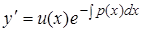 (6)
(6)
Здесь решение ищется в такой же форме, как для однородного уравнения, но вместо произвольной постоянной стоит функция 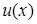 – новая неизвестная функция. Для ее определения подставляем y, определенное по (6), в (1).
– новая неизвестная функция. Для ее определения подставляем y, определенное по (6), в (1).
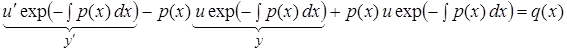 или
или 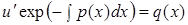 .
.
Отсюда 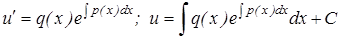
Следовательно, 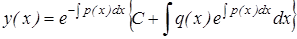 . (7)
. (7)
Это и есть общее решение уравнения (1). Оно содержит все решения. Особых решений нет.
Рассмотрим вопрос об отношении частного решения уравнения (1), удовлетворяющего начальному условию 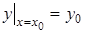 . (8)
. (8)
Теорема. Решением задачи Коши 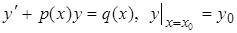 служит функция:
служит функция:
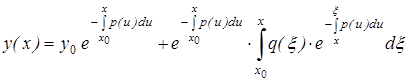 . (9)
. (9)
Замечания:
1. Формулу (9) можно записать короче, если 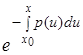 ввести под интеграл:
ввести под интеграл:
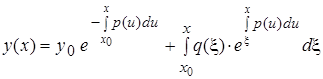 (10)
(10)
2. Если в формуле (10) 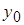 считать произвольной постоянной (при этом значение
считать произвольной постоянной (при этом значение 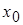 безразлично какое), то формула (10) определит общее решение уравнения (1).
безразлично какое), то формула (10) определит общее решение уравнения (1).
3. Запоминать формулу (10) не следует. Надо помнить способ получения формулы (7).
Примеры:
1. Найти общее решение уравнения 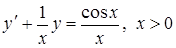
Решение. Здесь 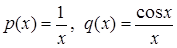 . Вычислим
. Вычислим 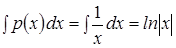 (С можно положить = 0).
(С можно положить = 0).
Положим 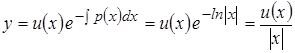 . Так как
. Так как 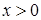 , то
, то 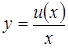 .
.
Подставляем в уравнение 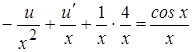 .
.
Отсюда 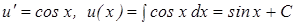 .
.
Следовательно, общее решение будет 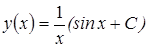
Теорема.(о структуре решения линейного неоднородного уравнения)
Общее решение линейного неоднородного уравнения состоит из суммы: какого-либо частного решения неоднородного уравнения и общего решения соответствующего ему однородного уравнения.
27. Уравнение Бернулли, его решение. Уравнение в полных дифференциалах и его решение.
Уравнением Бернулли называется уравнение вида
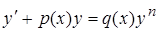 , (1)
, (1)
где n – любое число, не обязательно целое.
При 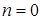 уравнение Бернулли превращается в линейное неоднородное уравнение. При
уравнение Бернулли превращается в линейное неоднородное уравнение. При 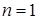 оно превращается в линейное однородное уравнение.
оно превращается в линейное однородное уравнение.
Таким образом, уравнение Бернулли служит некоторым обобщением линейных уравнений, в общем случае оно является нелинейным дифференциальным уравнением (при 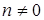 и
и 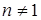 ).
).
Однако во всех случаях его решение тесно связано с решением линейного уравнения.
Теорема. Пусть 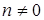 и
и 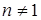 . Тогда уравнение Бернулли (1) подстановкою
. Тогда уравнение Бернулли (1) подстановкою 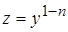 сводится к решению линейного уравнения (для функции z).
сводится к решению линейного уравнения (для функции z).
Замечание. Уравнение Бернулли (1) может быть решено другим способом. Введем вместо неизвестной функции 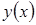 две неизвестные функции
две неизвестные функции 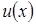 и
и 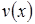 , такие, что
, такие, что 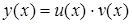 . (7)
. (7)
Подставляя это в уравнение (1), получим:
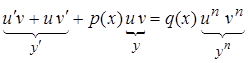 (8)
(8)
Из этого одного уравнения определить две функции u и v нельзя.
Для того, чтобы определить конкретные функции 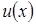 и
и 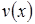 , необходимо задать еще одну зависимость между
, необходимо задать еще одну зависимость между 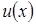 и
и 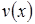 , причем вообще говоря, произвольную.
, причем вообще говоря, произвольную.
Но проще всего положить 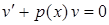 . (9)
. (9)
Тогда уравнение (8) примет вид: 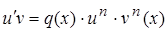 или, считая
или, считая 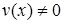 (или, что то же,
(или, что то же, 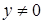 )
) 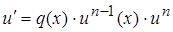 . (10)
. (10)
Так как 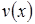 есть решение однородного линейного уравнения (9), то его можно считать его известным:
есть решение однородного линейного уравнения (9), то его можно считать его известным: 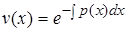 . (11)
. (11)
Здесь, при интегрировании уравнения (8), мы положили произвольную постоянную 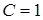 . Это можно делать, так как за функцию
. Это можно делать, так как за функцию 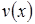 мы можем взять любое решение уравнения (9).
мы можем взять любое решение уравнения (9).
Итак, 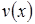 известно. Отсюда следует, что уравнение (10) для определения
известно. Отсюда следует, что уравнение (10) для определения 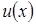 будет с разделяющимися переменными (считаем
будет с разделяющимися переменными (считаем 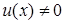 ). (12)
). (12)
Отсюда получаем 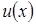 :
: 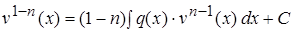 или
или 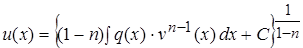 (13)
(13)
Формулы (11) и (13) позволяют построить решение уравнения Бернулли
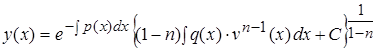 .
.
Такой способ решения годится и для и 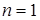 . В этом случае только формула (13) будет иметь другой вид, именно:
. В этом случае только формула (13) будет иметь другой вид, именно: 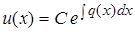 , где С – произвольная постоянная.
, где С – произвольная постоянная.
Пример. 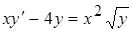 или
или 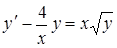 .
.
Это уравнение Бернулли. Здесь 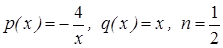 .
.
Преобразуем уравнение, разделив его на 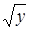 :
: 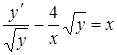 .
.
Положим 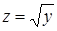 , тогда
, тогда 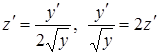 .
.
Следовательно, 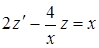 или
или 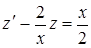 .
.
Отсюда 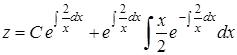 .
.
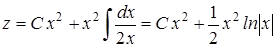 и
и 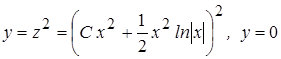 – особое решение.
– особое решение.
Дифференциальное уравнение вида
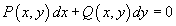
называется уравнением в полных дифференциалах, если существует такая функция двух переменных u(x,y) с непрерывными частными производными, что справедливо выражение
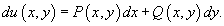
Общее решение уравнения в полных дифференциалах определяется формулой
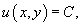
где C − произвольная постоянная.
