Вычисление объемов тел вращения с помощью интегралов.
Вычисление объема тела по известным площадям параллельных сечений.
Определение. Объем тела может быть вычислен по формуле 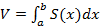 , где S(
, где S( 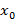 )-площадь попереного сечения тела T плоскостью x=
)-площадь попереного сечения тела T плоскостью x= 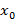 . в частности, если тело образовано вращением криволинейной трапеции вокруг оси Oх, то
. в частности, если тело образовано вращением криволинейной трапеции вокруг оси Oх, то 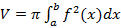 , а если вокруг оси Оу, то
, а если вокруг оси Оу, то 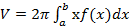 [5].
[5].
а) Тело и его объем. Произвольное ограниченное множество точек пространства будем называть телом.
Основные определения и утверждения, относящиеся к телам, аналогичны соответствующим определениям и утверждениям, содержащимся в главе 4 нашей курсовой работы. Поэтому некоторые утверждения для тел (см. теоремы 1 и 2) будут опущены.
По аналогии с понятием клеточной фигуры назовем тело клеточным, если его можно представить как объединение конечного числа непересекающихся параллелепипедов, т. е. тел вида М = {{x,y,z): 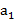 ≤ х ≤
≤ х ≤ 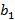 ,
, 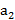 ≤у ≤
≤у ≤ 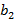 ,
, 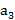 ≤ z ≤
≤ z ≤ 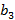 }, а также тел, получаемых из М удалением части границы (или всей границы) тела М. Объемом параллелепипеда М назовем число (
}, а также тел, получаемых из М удалением части границы (или всей границы) тела М. Объемом параллелепипеда М назовем число ( 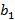 —
— 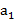 )(
)( 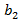 —
— 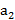 )(
)( 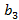 —
— 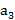 ), а объемом клеточного тела — сумму объемов составляющих его параллелепипедов[14].
), а объемом клеточного тела — сумму объемов составляющих его параллелепипедов[14].
Рассмотрим подробнее. Пусть требуется найти объем V тела (рис 14), причем известны площади сечений этого тела плоскостями, перпендикулярными некоторой оси, например оси Ox:S = S(x), a≤ x≤ b[13].
Рисунок 14.
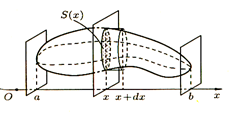
1. Через произвольную точку x 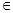 [а; b] проведем плоскость П, перпендикулярную оси Ох. Обозначим через S(x) площадь сечения тела этой плоскостью; S(x) считаем известной и непрерывно изменяющейся при изменении x. Через v(x) обозначим объем части тела, лежащее левее плоскости П. Будем считать, что на отрезке [а; x] величина v есть функция от x, т. е. v = у(x) (v(a) = 0, v(b) = V).
[а; b] проведем плоскость П, перпендикулярную оси Ох. Обозначим через S(x) площадь сечения тела этой плоскостью; S(x) считаем известной и непрерывно изменяющейся при изменении x. Через v(x) обозначим объем части тела, лежащее левее плоскости П. Будем считать, что на отрезке [а; x] величина v есть функция от x, т. е. v = у(x) (v(a) = 0, v(b) = V).
2. Находим дифференциал dV функции v = v(x). Он представляет собой
“элементарный слой” тела, заключенный между параллельными плоскостями, пересекающими ось Ох в точках x и x + Δx, который приближенно может быть принят за цилиндр с основанием S(x) и высотой dx. Поэтому дифференциал объема dV = S(х) dх.
3. Находим искомую величину V путем интегрирования dА в пределах от a до b:
V = 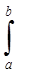 S(x) dx
S(x) dx
Объем тела вращения
Пусть функция f(x) непрерывна и неотрицательна на отрезке 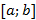 . Тогда тело, которое образуется вращением вокруг оси Ox криволинейной трапеции, ограниченной сверху графиком функции y=f(x), имеет объем
. Тогда тело, которое образуется вращением вокруг оси Ox криволинейной трапеции, ограниченной сверху графиком функции y=f(x), имеет объем
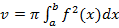 .
.
Рисунок 6 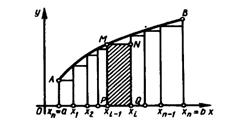
Доказательство. Разобьем произвольно отрезок [a;b] на n частей точками a= 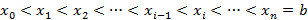 . На каждом частичном отрезке [
. На каждом частичном отрезке [ 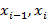 ] построим прямоугольник (рис. 15). При вращении вокруг оси Ox каждый прямоугольник опишет цилиндр. Найдем объем i-го цилиндра, образованного вращением прямоугольника PMNQ:
] построим прямоугольник (рис. 15). При вращении вокруг оси Ox каждый прямоугольник опишет цилиндр. Найдем объем i-го цилиндра, образованного вращением прямоугольника PMNQ:
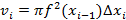 ,
,
где 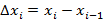 .
.
Сумма объемов всех n цилиндров приближенно равна объему данного тела вращения:
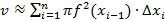 .
.
С другой стороны эта сумма является интегральной суммой для интеграла 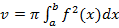 . Так как функция
. Так как функция 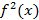 непрерывна на [a;b], то предел этой суммы при
непрерывна на [a;b], то предел этой суммы при
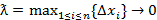 существует и равен определенному интегралу
существует и равен определенному интегралу 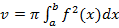 . Таким образом,
. Таким образом,
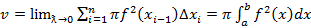 [15].
[15].
