Поверхности уровня определяются уравнением

ЭЛЕМЕНТЫ ТЕОРИИ ПОЛЯ

Электронное учебное пособие для студентов 2 – 3 курсов

всех специальностей заочной и дистанционной форм обучения

Шахты – 2003

Составитель:

кандидат физико-математических наук, доцент кафедры математики ЮРГУЭС В.И. Филиппенко

В пособии рассмотрены основные понятия теории поля: градиент, дивергенция, ротор, циркуляция. Даны приложения теорем Гаусса – Остроградского и Стокса. Указаны условия потенциальности и соленоидальности векторных полей. Приведены детальные решения типовых примеров на вычисление числовых характеристик векторного поля. Подобрано достаточное количество примеров для самостоятельного решения студентами.

Пособие предназначено для студентов-заочников ЮРГУЭС.

© Южно-Российский государственный университет экономики и сервиса. 2003

© Филиппенко В.И., 2003 г.

Содержание

Введение………….………………………………………………………………………………….4

1. Скалярные и векторные поля……………...…………………………………………………..……4

2. Циркуляция векторного поля вдоль кривой……………..…….......………………………………8

3. Формула Гаусса-Остроградского. Дивергенция……………………….………………..……….10

4. Формула Стокса……………………………………………………………………………….……14

5. Ротор векторного поля………………….…………...……………………………………………..16

6. Потенциальное поле и его свойства………………………………………………………………19

7. Соленоидальное поле и его свойства……………………………………………………………..22

8. Векторный потенциал…………………..…………………………………………………………23

Ответы………………………………………………………………………………………………25

Литература…………………………………………………………………………………………..27

ВВЕДЕНИЕ

Физика в своем историческом развитии постепенно превратилась из науки описательной в науку точную. Для характеристики различных явлений и процессов, происходящих в природе и технике, физики все шире используют математические методы, или, как принято говорить, соответствующий математический аппарат. Для этой цели пришлось прежде всего ввести меру каждого физического свойства. Пока физики имели дело с простейшими свойствами тел, в качестве меры каждого из них можно было ограничиться скалярными величинами, обычно показывающими, во сколько раз мера данного свойства рассматриваемого тела больше некоторого единичного масштаба. Так были введены такие скалярные величины, как длина, площадь, объем, масса, время, температура, электрический заряд, энергия и т.п.

Со временем выяснилось, что для количественного описания скорости движения, изменения этой скорости, взаимодействия тел и т.п. скалярные величины не подходят. В этих случаях оказались пригодными более сложные математические величины — направленные отрезки, или векторы. Развитие количественных методов показало, что одно и то же физическое свойство в разных точках исследуемого объекта может принимать различные значения, и поэтому для их математического описания необходимо знать совокупность значений соответствующей величины во всех точках рассматриваемого объекта. Так в физике постепенно сложилось представление о математическом поле – области пространства, каждой точке которого соответствует определенное значение некоторой физической величины.

Поля бывают скалярные и векторные. Каждое из них в свою очередь может быть стационарным (если физическая величина в каждой точке области со временем не меняется) или нестационарным. Введение понятия поля в физике сыграло такую же прогрессивную роль, как в свое время появление в математике переменной величины.

1. Скалярные и векторные поля

Множество Е точек рассматриваемого пространства, совместно с приписанными этим точкам числами, называется скалярным полем. Скалярным полем часто называют и саму функцию F(M), породившую это поле на точечном множестве Е. Если Е – множество точек на плоскости, то скалярное поле называется плоским; если же Е – множество точек в трехмерном пространстве, то поле называется пространственным.

Примеры скалярных полей различной природы доставляет нам физика. Так, можно говорить о скалярном поле температур в пространстве, занятом нагретым телом (в каждой точке этого пространства температура имеет определенное значение); можно говорить о скалярном поле электрического потенциала в пространстве вокруг электрического заряда и т.п. Известные из физики изотермы (линии равной температуры), изобары (линии равного давления), эквипотенциальные линии (линии равного потенциала) являются примером линий уровня в различных плоских физических скалярных полях.

Для пространственного скалярного поля F(M) = F(x,y,z) уравнение F(x,y,z) = С с переменным параметром С определяет семейство поверхностей уровня, т.е. семейство поверхностей во всех точках каждойиз которых скалярное поле F(М) имеет одно и тоже значение. Поверхности уровня могут вырождаться в линии и точки. Для сферически симметричного поля, т.е. такого, что значение F(М) зависит только от расстояния точки М до некоторой фиксированной точки N, любая сфера с центром в точке N является поверхностью уровня. Если F(М) = const во всей области Е, то множество точек, удовлетворяющих уравнению F(x,y,z) = С, либо пусто, либо совпадает со всей областью Е.

Градиент скалярного поля u(M) = u(x,y,z) определяется равенством

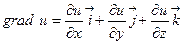. (1)

В математической теории поля широко используют символическое выражение, обозначаемое 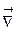("набла"): 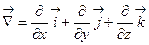, напоминающее по формевектор, разложенный по базисным ортам 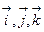, где вместо координат вектора записаны операторы дифференцирования 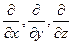. Это выражение называют векторным дифференциальным оператором или оператором Гамильтона.

Если каждой точке М данной области Е соответствует определенный вектор 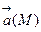, то говорят, что в области Е задано векторное поле. В декартовой системе координат векторное поле 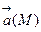задается тремя функциями P,Q,R, определенными в области Е

.

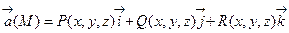Здесь и в дальнейшем будем предполагать, что эти функции во всей области непрерывны вместе с частными производными. Для плоского векторного поля:

.

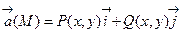Векторной линией данного поля 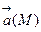называют такую линию ℓ, в каждой точке которой вектор 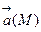имеет направление касательной к этой линии. Через каждую точку векторного поля проходит (при условии, что 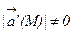)одна векторная линия. Совокупность всех векторных линий определяется системой дифференциальных уравнений:

.

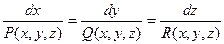Векторные линии характеризуют векторные поля геометрически и дают известную информацию о структуре этого поля. Так, если 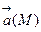– стационарное поле скоростей текущей жидкости, то в этом поле векторные линии, очевидно, будут являться траекториями частиц жидкости; называются они в таком случае линиями тока. В векторном поле 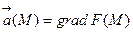векторные линии нормальны в каждой точке поверхностям уровня F(x,y,z) = С; вдоль этих линий функция F(M) изменяется быстрее всего. В случае плоского векторного поля семейство векторных линий определяется уравнением

.

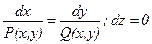Примеры

1. Найти линии уровня плоского поля u=xy.

Решение. Линии уровня определяются уравнением xy=С и представляют собой равносторонние гиперболы. При С = 0 линиями уровня являются координатные оси Ох и Оу.

2. Найти поверхности уровня скалярного поля:

.

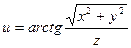Решение. Поверхности уровня определяются уравнением 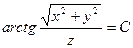. Отсюда находим 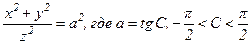. Мы видим, что поверхностями уровня являются круговые конусы x²+y²-a²z² = 0, ось симметрии которых совпадает с осью Оz.

3. Найти поверхности уровня скалярного поля:

.

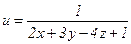Решение. Скалярное поле определено для всех точек пространства, кроме точек, расположенных на плоскости:

2x + 3y – 4z + 1 = 0

Упражнения

В следующих задачах установить область определения и найти линии и поверхности уровня скалярного поля:

10. .

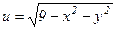11. .

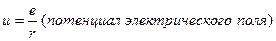12. .

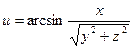13. .

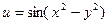14. .

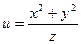15. Найти градиент скалярного поля:

а) .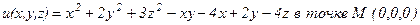

б) .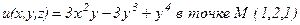

в) .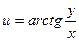

16. Найти векторные линии сферически симметричного поля.

17. Найти векторные линии поля .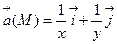

18. Найти векторные линии поля .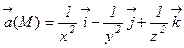

19. Найти уравнения семейства векторных линий поля: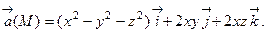

20. Найти векторные линии поля 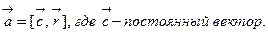( 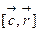– векторное произведение ).

21. Найти силовые линии:

а) магнитного поля прямолинейного тока;

б) гравитационного поля точечного источника.

22. Поток несжимаемой жидкости имеет потенциал 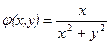. Найти траектории движения частиц жидкости.

23. В точке (0;0) найти направление, в котором функция z=xsiny + ycosx изменяется быстрее всего.

24.1) Найти наибольшую крутизну подъема поверхности z=ln(x²+4y²) в точке (6; 4; ln100).

2) Найти наибольшую крутизну подъема поверхности z=x^y в точке (2; 2; 4).

25. Каково направление наибольшего изменения функции

j(x,y,z)=xsinz – ycosz в начале координат?

Рис. 1.

26.1) 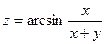. Найти угол между градиентами этой функции в точках (1; 1) и (3; 4).

2) Даны функции 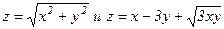. Найти угол

между градиентами этих функций в точке (3; 4).

Примеры

27. Вычислить циркуляцию плоского векторного поля 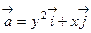вдоль кривой x=3cost, y=sint с

обходом по часовой стрелке.

Решение. Данная кривая является эллипсом. Обход кривой совершается по часовой стрелке, поэтому t меняется от 2p до 0. Следовательно, циркуляция вычисляется следующим образом: 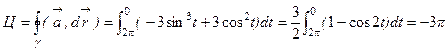. Ответ: –3p

28. Вычислить циркуляцию вектора 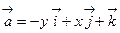вдоль окружности 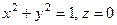в положительном направлении.

Решение. Параметрическое уравнение окружности: x=cost, y=sint, z=0, 0 £ t £ 2p. Поскольку P = –y =

= ‑sint, Q=x=cost, R=1, dx= –sintdt, dy=costdt, dz=0, то по определению циркуляции получаем:

.

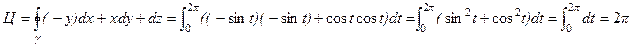Ответ: 2p

29. Найти циркуляцию векторного поля 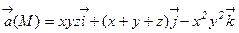вдоль контура квадрата

ABCDA, определяемого уравнениями: –x+y=a; x+y=a; x–y=a; x+y=–a; z=0. См. рис. 2.

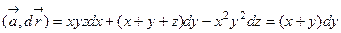Решение. Имеем: , так как z=0 и dz=0. Разбиваем искомую циркуляцию на четыре линейных интеграла, причем в качестве параметра на каждой стороне квадрата выбираем координату y:

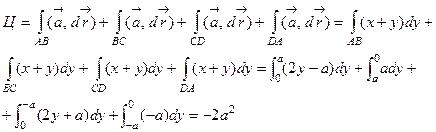
Ответ: –2а².

Упражнения

30. Найти циркуляцию поля 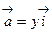по контуру окружности x=bcost, y=b+bsint, расположенной в плоскости ХОY.

31. Найти циркуляцию векторного поля 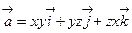вдоль окружности x²+y²=R²; z=0.

32. Вычислить циркуляцию поля 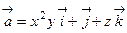вдоль окружности x²+y²=R, z=0.

33. Найти циркуляцию Ц вектора :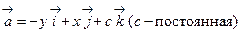

а) вдоль окружности x²+y²=1, z=0;

б) вдоль окружности (x–2)²+y²=1, z=0.

Примеры

34. Пользуясь формулой Остроградского-Гаусса, вычислить интеграл 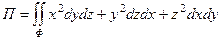, где Ф – внешняя сторона сферы (x–a)²+(y-b)²+(z–c)²=R².

Решение. По формуле Остроградского-Гаусса имеем:

,

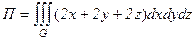где G – шар (x–a)²+(y-b)²+(z–c)²£R². Для вычисления интеграла перейдем к сферическим координатам:

x=a+rcosjsinq, y=b+rsinjsinq, z=c+rcosq, 0 £ j £ 2p, 0 £ q £ p.

Якобиан перехода равен r²sinq. Уравнение границы области G имеет вид r = R. Следовательно, .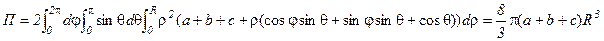

Ответ: .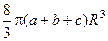

Пусть задана ориентированная поверхность (Ф), т.е. такая поверхность, в каждой точке которой выбран единичный вектор 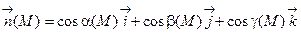, меняющийся на поверхности непрерывно. В случае замкнутой поверхности в качестве 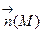будем всегда выбирать вектор внешней нормали.

Потоком П векторного поля 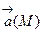через ориентированную поверхность (Ф) называют поверхностный интеграл (первого рода): .

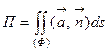Дивергенция (расходимость) векторного поля 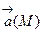может быть определена выражением: 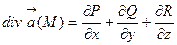, т.е. дивергенция векторного поля 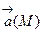представляет собой скалярное поле в области G.

Если 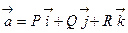– разложение векторного поля 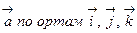, то формулу, определяющую поток, можно записать в виде:

,

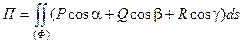либо записать в форме поверхностного интеграла (второго рода):

.

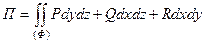Теперь теорему Остроградского-Гаусса можно сформулировать следующим образом: поток векторного поля через замкнутую поверхность равен тройному интегралу от дивергенции векторного поля по объему, ограниченному этой поверхностью.

35. Найти поток векторного поля 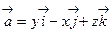через замкнутую поверхность (Ф), состоящую из поверхности конуса x²+y²=z² и плоскости z=1. См. рис 3.

Решение. Имеем .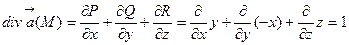

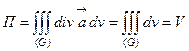Следовательно, , где V–объем конуса.

Так как 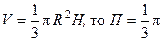. Ответ: p/3.

36. Найти поток векторного поля 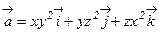через поверхность сферы x²+y²+z²=R².

Решение. В данном случае поверхность (Ф) – замкнутая, поэтому для вычисления потока можно применить формулу Гаусса - Остроградского. Имеем

.

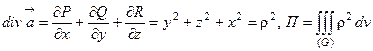Рис. 3.

Вычисляем интеграл в сферических координатах:

.

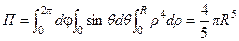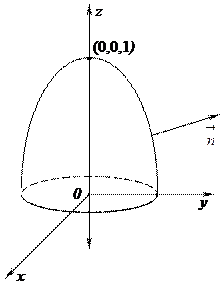
37. Найти поток векторного поля 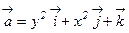через часть поверхности параболоида 1 – z = x²+y² (0 £ z £ 1). См. рис. 4.

Решение. Обозначим данную поверхность через (Ф₁) и рассмотрим замкнутую поверхность 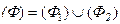, где (Ф₂) – круг радиуса R=1 на плоскости XOY. Из формулы Гаусса - Остроградского вытекает, что поток через поверхность (Ф) равен нулю. Действительно, для данного поля

.

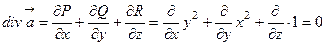Рис. 4

Следовательно, 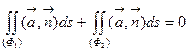. Отсюда искомый поток через поверхность (Ф₁):

.

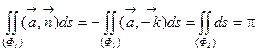Ответ: p.

38. Пользуясь формулой Остроградского-Гаусса, вычислить поток векторного поля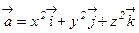

через полную поверхность конуса .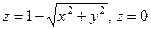

Решение. Найдем дивергенцию векторного поля: 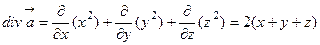. Тогда .

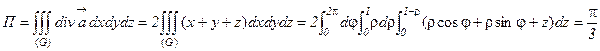Упражнения

Применяя формулу Остроградского-Гаусса, преобразовать поверхностные интегралы в интегралы по объему:

39. .

40. .

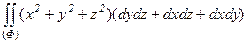41.

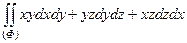
С помощью формулы Остроградского-Гаусса вычислить следующие интегралы:

42.

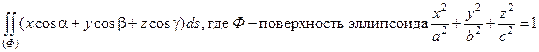
43.

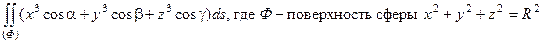
44.

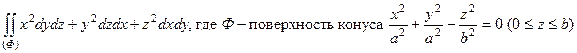
45. Найти дивергенцию вектора .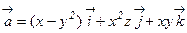

46. Пользуясь формулой Остроградского-Гаусса, преобразовать поверхностный интеграл

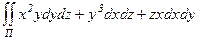в интеграл по объему.

47. Вычислить поверхностный интеграл 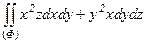, где Ф – полная поверхность параболоида z=x²+y², ограниченного плоскостью z=1.

48. Пользуясь формулой Остроградского–Гаусса, вычислить поверхностные интегралы по внешней стороне поверхности Ф (если поверхность не замкнутая, дополните её до замкнутой).

а) ;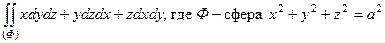

б) ;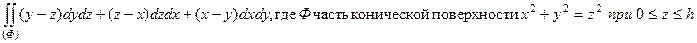

в) ;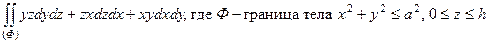

г) ;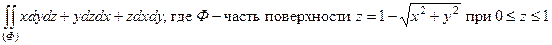

д) 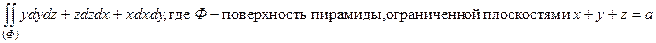(a>0), x=0, y=0, z=0;

е) ;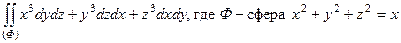

ж) .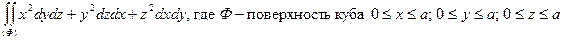

Формула Стокса

Пусть в области G определено векторное поле 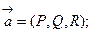L – замкнутый контур, лежащий в области G; Ф- произвольная поверхность, границей которой является контур L; ФÌG (говорят "поверхность Ф натянута на контур L"); 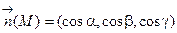–единичный вектор нормали на выбранной стороне поверхности Ф.

Поверхность Ф называется xyz – проектируемой, если она однозначно проектируется на каждую координатную плоскость прямоугольной системы координат Oxyz. Такую поверхность можно задать с помощью любого из уравнений: z=z(x,y), (x,y)Î G₁; x=x(y,z), (y,z)ÎG₂; y=y(z,x), (z,x)Î G₃.

Пусть Ф – гладкая xyz – проектируемая ориентированная поверхность, ограниченная кусочно-гладким контуром L и расположенная внутри области G, в которой функции P(x,y,z), Q(x,y,z), R(x,y,z) имеет непрерывные частные производные первого порядка. Тогда справедлива формула Стокса

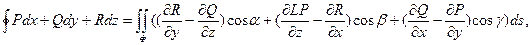
где ориентация контура L согласована с ориентацией поверхности Ф. Левая часть формулы Стокса есть циркуляция векторного поля вдоль контура L, а правая часть представляет собой поток через поверх

ность Ф векторного поля с координатами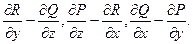

Эта формула названа по имени английского физика и математика Д. Стокса. Её формулу можно переписать также в следующем виде:

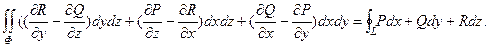
Формула Стокса остается верной для иной ориентированной поверхности Ф с кусочно-гладким краем L , которую можно разбить при помощи кусочно-гладких линий на конечное число гладких кусков, проецирующихся на все три плоскости координат. Ориентированная поверхность, которую можно разбить на конечное число и плоского треугольников, называется полиэдральной поверхностью и представляет собой пример простейшей поверхности, к которой применима формула Стокса.

Примеры

49. Вычислить циркуляцию вектора 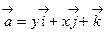вдоль окружности x²+y²=1, z=0 в положительном направлении.

Решение. В этом случае P=y; Q=x; R=1. Следовательно,

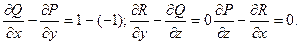
по формуле Стокса

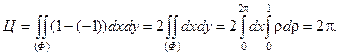
Применяя формулу Стокса, вычислить интегралы:

50 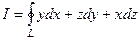, где L - окружность x²+y²+z² a², x+y+z=0, пробегаемая против хода часовой стрелки, если смотреть с положительной оси Ox.

Решение. Применив формулу Стокса и взяв в ней в качестве поверхности Ф круг радиуса а, лежащий в плоскости x+y+z=0, получаем:

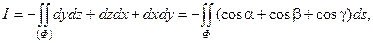
где 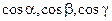- направляющие косинусы нормали к поверхности Ф – плоскости x+y+z=0, так как нормаль этой плоскости образует с положительным направлением оси Oz острый угол, то в каждой из формул для вычисления 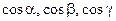перед знаком радикала возьмем знак "+".

Очевидно, 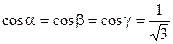, в силу чего имеем:

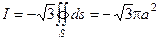
Ответ: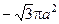

51. 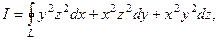L - замкнутая кривая x=acost, y=acos2t, z=acos3t, пробегается в направлении возрастания параметра t.

Решение. При изменении t от 0 до p подвижная точка М(x,y,z) пробегает кривую L от точки M₀(a_,a_,a) до точки M₁(-a_,a_,-a), а при изменении t от p до 2p точка М пробегает ту же самую часть кривой L в противоположном направлении – от точки М, до точки М₀. Таким образом, точки замкнутой кривой L взаимно накладываются и кривая L не ограничивает никакой поверхности, вследствие чего I=0.

Ответ: 0.

Упражнения

52. Интеграл 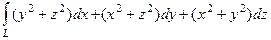, взятый по некоторому замкнутому контуру, преобразовать с помощью формулы Стокса в интеграл по поверхности, "натянутой" на этот контур.

53. Вычислить интеграл 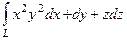, где контур L – окружность x²+y²= R², z=0, используя формулу Стокса, взяв в качестве поверхности полусферу 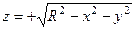. Интегрирование по окружности в плоскости xOy ведется в положительном направлении.

Ротор векторного поля

С понятием циркуляции тесно связано понятие ротора, или вихря. Циркуляция характеризует завихренность векторного поля вдоль всего контура. Локальной характеристикой поля, связанной с завихренностью, является ротор.

Рассмотрим сначала плоское векторное поле и какой-то контур L , окружающий выбранную точку М₀. Величину площади области, заключенной внутри L, обозначим через S. Тогда отношение

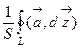(1)

дает среднюю плотность циркуляции вектора на площадке S. Плотность циркуляции в точке М₀ характеризуется пределом выражения (1) при условии стягивания контура L в точку М₀, тогда площадь S, охватываемая контуром L, стремится к нулю, таким образом, если предел 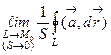существует, то он дает величину завихренности поля в точке М₀.

Если векторное поле - пространственное, то можно говорить о завихренности поля в каком-либо направлении .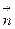

Ротором векторного поля в точке М₀ обозначаемым 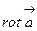называется вектор, проекция которого на каждое направление 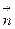равна пределу отношения циркуляции векторного поля по контуру L плоской области G, перпендикулярной этому направлению, к величине площади S этой области, когда размеры площади стремятся к нулю, а сама область стягивается в точку М₀, т.е.

,

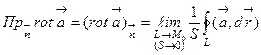где L – контур, лежащий в плоскости, перпендикулярной вектору 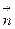, S- площадь области, ограниченной этим контуром.

Если задано векторное поле 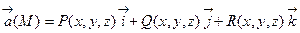, где функции P, Q и R – непре

рывно дифференцируемые в соответствующей области , то

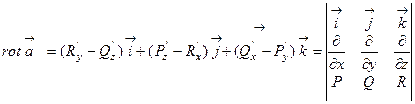
Примеры

54. Найти ротор векторного поля .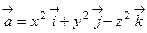

Решение. 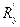= = 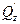= = 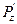= =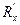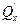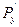0, то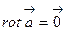

Ответ: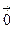

55. Найти rot (grad u), если u=x²+ y²+ z²

Решение. Поскольку grad u = 2x² + 2y² +2z² , то rot (grad u)=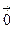

Ответ: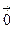

56. Найти ротор поля скоростей твердого тела, вращающегося вокруг неподвижной точки с мгновенной угловой скоростью .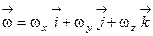

Решение. Как известно, скорость твердого тела определяется по формуле

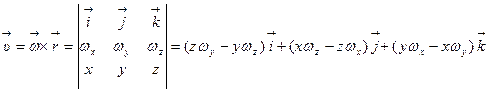
Отсюда находим .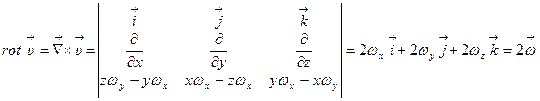

Таким образом, 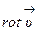, характеризуя "вращательную компоненту" поля скоростей, равен удвоенной скорости вращения.

57. Доказать, что завихренность поля достигает наибольшего значения в направлении ротора.

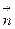Решение. Завихренность поля в направлении равна проекции ротора на это направление, т.е. 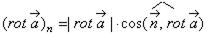.Отсюда видно, что поле наибольшую завихренность имеет в случае, когда 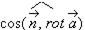=1, а это означает, что направление нормали 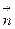совпадает с направлением 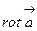, причем наибольшая завихренность равна .

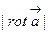58. Вычислить ротор векторного поля: = y² - x² +z² .

Решение .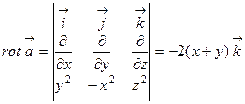

Ответ: .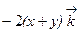

Упражнения

59. Доказать свойства ротора:

а) 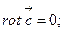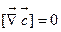, где 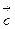=const

б)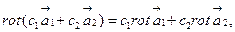

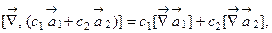где с₁, с₂ – постоянные коэффициенты.

в) 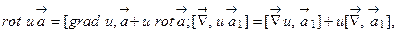где u - скалярное поле.

60. Вычислить ротор векторного поля:

а)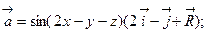

б)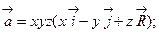

в)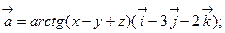

61. Вычислить ротор векторного поля 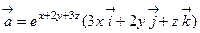в точке М₀(3,-3,1).

62. Найти функцию векторного поля 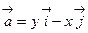вдоль замкнутой линии ABОA, где АВ – дуга астроиды, определяемой уравнением: 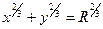или x=Rcos³t, y=Rsin³t.

Указание. Следует применить формулу Стокса:

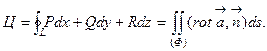
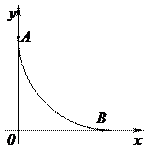Рис. 4.

3. С помощью формулы Стокса найти циркуляцию векторного поля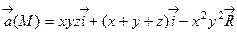

вдоль контура квадрата АВСDА определяемого уравнениями: –x+y=a; x+y=a; x–y=a; x+y=–a; z=0.

64. Вычислить с помощью формулы Стокса циркуляцию векторного поля 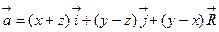вдоль окружностей:

а) (y+1)² +(z–1)²=1, x=5 (вектор положительной нормали );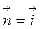

б) (x–3)² +(y–2)²=4, z=0 (вектор положительной нормали )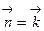

65. Доказать, что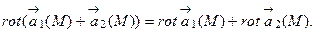

Примеры

66. Проверить, что поле =(y+z) + (z+x) +(x+y) является потенциальным, и найти его потенциал.

Решение. Поле определено во всем пространстве, т.е. в односвязной области, поэтому достаточно проверить, что rot =0. Имеем:

rot = =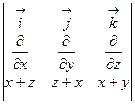(1–1) +(1–1) +(1–1) = ,

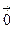что и доказывает потенциальный характер поля .

Найдем потенциал двумя способами.

1 способ.

Для нахождения потенциала воспользуемся формулой (*), беря в качестве М₀ начало координат:

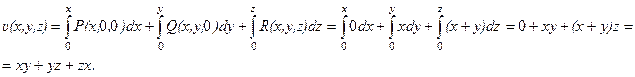
2 способ.

Будем снова считать М₀(0,0,0).

Пусть 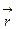=x +y +z – радиус-вектор точки М(x,y,z), а точка N пробегает отрезок M₀М; ее радиус‑вектор 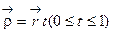. Точка N имеет координаты t_x, t_y, t_z.

Отсюда d 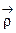= 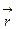dt. Положим .

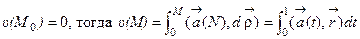Для рассматриваемого поля (t)=t(y+z) + t(z+x) +t(x+y) .

( (t), 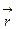)=t(y+z)x+t(z+x)y+t(x+y)z=2t(xy+yz+zx).

Следовательно, 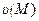=(xy+yz+zx) 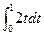= xy+yz+zx.

Ответ: xy+yz+zx.

67. Доказать, что циркуляция потенциального поля по любому замкнутому контуру равна нулю.

Решение: Пусть - потенциальное поле и (L) - замкнутый контур, началом и концом которого является точка М(М=М₀).

Тогда 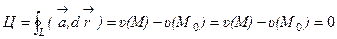, что и требовалось доказать.

Упражнения

68. Пусть 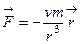– гравитационное поле (поле сил тяготения), которое представляет собой силу притяжения единичной массы, помещенной в точку М, массой m, находящийся в начале координат. Сила определена во всех точках, кроме начала координат и образует векторное поле – поле тяготения точечной массы m. Показать, что поле 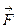потенциально во всем пространстве, кроме начала координат и найти его потенциал.

69. Проверить , что поле =(3yz+x²) + (2y²+3xz) +(z²+3xy) является потенциальным, и найти его потенциал.

70. Доказать, что векторное поле = y² +2xy +z потенциально, и найти его потенциал.

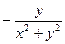
71. Выяснить, является ли векторное поле = + +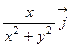2 потенциальным.

72. Даны векторные поля: ₁=(y+z) + (x+z) +(x+y) ; ₂=f(x) + f₂(y) + f₃(z) ; ₃=x + y +y .

Выяснить какие из них являются потенциальными.

73. Проверить, будет ли потенциальным поле