Статистическая обработка ряда наблюдений

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

по выполнению лабораторных работ по курсу

«Математической обработки результатов наблюдений»

Москва, 2017 г.

Лабораторная работа № 1

Статистическая обработка ряда наблюдений

Точечное оценивание параметров.

Пример решения лабораторной работы.

Задан ряд невязок (в секундах) в треугольниках триангуляции II класса общим объемом 50:

- 1,81;	- 1,82;	+ 2,32;	0,00;	- 0,70;
+ 1,51;	+ 0,61;	- 1,29;	- 2,64;	+ 0,04;
+ 0,01;	+ 0,11;	+1,56;	- 1,09;	+ 2,78;
- 0,35;	- 0,01;	+ 1,64;	- 0,77;	- 1,26;
- 0,52;	- 0,69;	+ 1,02;	- 1,58;	+ 1,78;
+ 0,16;	+ 0,64;	+ 0,42;	+ 0,99;	- 2,08;
- 0,55;	+ 0,64;	- 0,09;	+ 0,56;	- 0,35;
- 2,55;	- 0,76;	+ 1,05;	- 1,51;	+2,71;
+ 0,70;	- 0,40;	+ 2,22;	- 1,14;	- 0,17;
- 0,31;	- 0,01;	+ 0,21;	+ 1,32;	- 0,85.

Рассматривая этот ряд невязок как выборку из некоторой генеральной совокупности ошибок суммы измеренных углов треугольников триангуляции, необходимо рассчитать точечные оценки математического ожидания, дисперсии, среднего квадратического отклонения, асимметрии и эксцесса. Решение выполнить по предварительно группированным данным.

Решение.

В качестве границ интервалов групп здесь принимают следующие значения: - 3,5"; - 2,5"; -1,5"; - 0,5"; + 0,5"; + 1,5"; + 2,5"; + 3,5". Тогда центрами интервалов будут значения: - 3,0"; -2,0";
- 1,0"; -0,0"; + 1,0"; + 2,0"; + 3,0". Все расчеты сведены в табл. 1.

После заполнения таблицы вычислены оценки по формулам:

1. Математического ожидания

M(х) = a =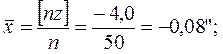

2. Дисперсии

D(x) =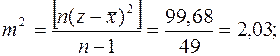

3. Среднего квадратического отклонения

σ =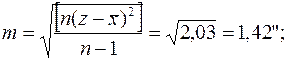

4. Третьего центрального момента

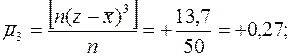
5. Асимметрии

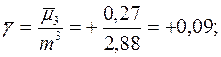
6. Четвертого центрального момента

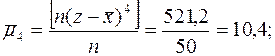
7. Эксцесса

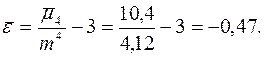
Таблица 1

№	Грани-цы интер-валов	Сорти-ровка	ni	Центры интер-валов zi	zini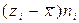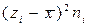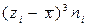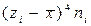
	- 3,5
		- 3,0	- 6,0	-2,92	-5,84	17,05	-49,8	145,0
	- 2,5
		- 2,0	-12,0	-1,92	-11,52	22,12	-42,5	81,5
	- 1,5
		- 1,0	-11,0	-0,92	-10,12	9,31	-8,6	7,9
	- 0,5
		0,0	0,0	+0,08	+1,20	0,10	-0,1	0,0
	+ 0,5
		+ 1,0	+9,0	+1,08	+9,72	10,50	+11,3	12,2
	+ 1,5
		+ 2,0	+10,0	+2,08	+10,40	21,63	+45,0	94,6
	+ 2,5
		+ 3,0	+6,0	+3,08	+6,16	18,97	+58,4	180,0
	+ 3,5
Σ					- 4,0			99,68	+13,7	521,2

Доверительное оценивание параметров.

По данным приведенного выше примера построить доверительные интервалы для математического ожидания, дисперсии и среднего квадратического отклонения при уровне значимости
α = 0,05.

Решение.

Из решения, приведенного выше, имеем 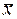= - 0,08, 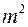= 2,03 и m = 1,42.

Для расчета доверительных границ математического ожидания из таблиц распределения Стьюдента найден tq. При этом учтено, что число степеней свободы ν = n – 1 = 49, а уровень значимости
α задан равным 0,05. Выбор tq произведен по данным таблицы распределения Стьюдента (Приложение 3) по двухсторонней критической области tq= 2,01. Доверительные границы найдены по формулам:

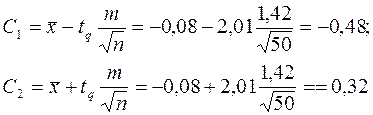
Доверительный интервал математического ожидания имеет вид:

- 0,48 < M(X) < + 0,32.

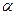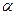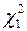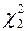Для нахождения доверительных границ дисперсии по вероятностям Р₂ = 1 - /2 = 0,975 и Р₁ = /2 = 0,025 и числу степеней свободы ν = n – 1 = 49, использованы таблицы критических точек распределения χ² величины и , которые оказываются равными 31,6 и 70,2. Расчет границ доверительного интервала дисперсии произведен по формулам:

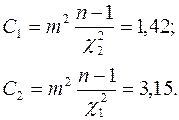
Доверительный интервал для дисперсии имеет вид:

1,42 < D(X) < 315.

Используя данные расчетов п.2, по формулам:

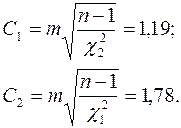
получены доверительные границы среднего квадратического отклонения.

Доверительный интервал для среднего квадратического отклонения имеет вид:

.

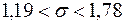Проверка статистических гипотез.

По данным приведенного выше примера проверить гипотезу о нормальном распределении невязок в треугольниках триангуляции II класса.

Решение.

Первым шагом решения задачи по проверке статистических гипотез о законе распределения является группировка исходных данных. Рекомендуется так подбирать границы интервалов, чтобы число попаданий в каждый интервал было не менее 5.

Руководствуясь этим правилом и используя результаты группировки, выполненные при решении приведенного выше примера, в качестве границ интервалов выбраны следующие значения: - ∞ ;- 1,5; - 0,5; + 0,5; + 1,5; + ∞ .Тогда число попаданий в каждый интервал соответственно равны 8, 11, 15, 9, 7. Для расчета теоретического числа попаданий в каждый обозначенный интервал, соответствующих нормальному распределению, рассчитаны центрированные, нормированные границы интервалов. Центрирование границ произведены с помощью оценки математического ожидания
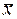= - 0,08, а нормирование – с помощью оценки среднего квадратического отклонения т = 1,42. Окончательный расчет центрированных, нормированных значений границ интервалов произведен по формуле:

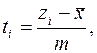
где z_i – выбранное значение границы интервала; t_i - центрированное, нормированное значение той же границы интервала.

По центрированным, нормированным значениям границ интервалов из таблиц распределения функции Лапласа (Приложение 1) найдены значения функции нормального распределения. Затем по формуле 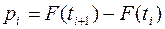найдены вероятность попадания в i – ый интервал, а по формуле 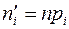- теоретическое число попаданий в тот же интервал.

Контроль вычислений - .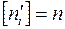

Для подсчета меры расхождения практического и теоретического числа попаданий вычислены для каждого интервала величины 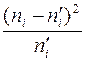. Их сумма дает величину меры расхождения 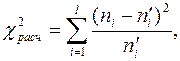где l – число групп. Все вычисления проведены в табл. 2.

В результате проведенных вычислений получена общая расчетная мера расхождения практического и теоретического числа попаданий χ²_расч, которая оказалась равной 0,298. Окончательное решение вопроса о согласованности опытных данных с выдвигаемой гипотезой нормального распределении угловых невязок принимается по результатам сравнения расчетной меры расхождения с предельно возможной. Предельно возможное значение меры расхождения (критическое значение) χ²_кр находят по таблицам распределения χ² по уровню значимости α = 0,05 и числу степеней свободы ν = l – c – 1 (Приложение 2). В приведенной формуле l – число интервалов группировки, в данном случае равное 5, c – число ранее определенных параметров, которые использовались при расчетах, проводимых в табл. 1. При расчетах центрированных, нормированных значений границ интервалов были использованы ранее вычисленные значения оценок математического ожидания 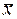и среднего квадратического отклонения т. Следовательно, в данном случае c = 2. Тогда число степеней свободы также равно 2.

Значение χ²_кр , выбранное из таблиц, равно 6,0. В этом случае χ²_расч < χ²_кр , что дает право делать вывод о хорошем согласовании результатов опыта с выдвинутой гипотезой о нормальном распределении невязок в треугольниках триангуляции II класса.

Таблица 2

№	Границы интервалов	Центр. норм. границы интерв.	F(ti)	pi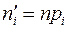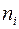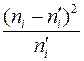
	- ∞	- ∞	0,0000
0,1587	7,9350		0,003
	- 1,5	- 1,00	0,1587
0,2234	11,1700		0,003
	- 0,5	- 0,30	0,3821
0,2770	13,8500		0,095
	+ 0,5	+ 0,41	0,6591
0,2074	10,3700		0,181
	+ 1,5	+ 1,11	0,8665
0,1335	6,6750		0,016
	+ ∞	+ ∞	1,0000
				1,0000	50,0000		0,298

Контрольная задача 1

Для исследования точности измерения линий светодальномером тахеометра 2ТА-5М было проведено 120 измерений на эталонном полигоне. Линии полигона ранее были измерены со значительно более высокой точностью, поэтому их значения можно принять за точные. Расхождения между эталонными значениями и значениями измерений линий светодальномером представляют собой ошибки светодальномерных измерений. Необходимо:

1. Построить гистограмму.

2. Вычислить оценки математического ожидания, дисперсии, среднего квадратического отклонения, асимметрии и эксцесса.

3. Построить доверительные интервалы для математического ожидания, дисперсии и среднего квадратического отклонения.

4. Проверить гипотезу о нормальном распределении ошибок светодальномерных измерений.

В табл. 3 приведены ошибки светодальномерных измерений. Значения ошибок даны в миллиметрах.

Таблица 3

№		№		№		№		№		№
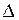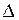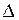	+ 14		+ 5		- 1		+ 2				+ 12
	+ 3		- 2		+ 2		+ 9		- 3		+ 6
	- 4		+ 14		+ 14		- 1		+ 5		- 5
	- 4		+ 11		- 6		- 6		+ 6		- 7
	+ 4		+ 2		- 4		+ 14		- 9		+ 4
	- 10		+ 6		- 8		- 2		+ 9		+ 3
	- 11		- 1		+ 2		+ 7		- 2		+ 4
	+ 6		- 12		+ 2		+ 3		- 11		+ 13
	- 4		- 2		+ 5		+ 2		+ 8		+ 3
	- 3		+ 4		+ 10				- 5		+ 6
	- 1		+ 8		+ 5		- 9		- 2		- 4
	+ 1		+ 10		- 4		+ 3		- 7
	+ 6		- 10		- 2		- 1		+ 1		+ 14
	+ 5		- 4		+ 5		- 9		- 14		+ 3
	- 13		+ 10		- 1		- 4		+ 7		+ 3
	+ 4		+ 2		+ 9		- 3		- 11		+ 6
	+3		- 10		+19		- 9		+ 8		+ 11
	+ 4		- 13		+ 6		- 6		+ 9		+ 2
	- 1		- 2		- 10		- 4		- 5		+ 2
	+ 5		- 8		+ 12		- 9				+ 4

Варианты для контрольной задачи 1

В каждом варианте необходимо вычеркнуть 20 элементов с соответствующими номерами:

№№ варианта	№№ вычеркиваемых элементов	№№ варианта	№№ вычеркиваемых элементов
	1-10; 21-30		21-30; 81-90
	1-10; 31-40		21-30; 91-100
	1-10; 41-60		21-30; 101-110
	1-10; 51-60		21-30; 111-120
	1-10; 61-70		31-40; 41-50
	1-10; 71-80		31-40; 51-60
	1-10; 81-90		31-40; 61-70
	1-10; 91-100		31-40; 71-80
	1-10; 101-110		31-40; 81-90
	1-10; 111-120		31-40; 91-100
	11-20; 21-30		31-40; 101-110
	11-20; 31-40		31-40; 111-120
	11-20; 41-50		41-50; 51-60
	11-20; 51-60		41-50; 61-70
	11-20; 61-70		41-50; 71-80
	11-20; 71-80		41-50; 81-90
	11-20; 81-90		41-50; 91-100
	11-20; 91-100		41-50; 101-110
	11-20; 101-110		41-50; 111-120
	11-20; 111-120		51-60; 61-70
	21-30; 31-40		51-60; 71-80
	21-30; 41-50		51-60; 81-90
	21-30; 51-60		51-60; 91-100
	21-30; 61-70		51-60; 101-110
	21-30; 71-80		51-60; 111-120

Лабораторная работа № 2

Уравнения регрессии

Пример решения лабораторной работы.

На геодезическом пункте одновременно выполнялись измерения угла двумя теодолитами, из которых один был установлен на сигнале, а второй – на штативе под сигналом. При этом получены результаты:

	№№ наблюдений
Сигнал, 57º 21ʹ 40"	3,21	2,21	2,11	2,49	3,19	3,29	4,41	2,67	0,75	2,20
Штатив, 57º 21ʹ 40"	5,10	4,02	3,22	2,57	3,62	4,93	6,53	4,59	2,84	3,46

Вычислить оценку коэффициента корреляции между наблюдениями на сигнале и на штативе и построить уравнение регрессии значения угла, измеренного на штативе в зависимости от значения угла, полученного на сигнале.

Решение.

Таблица 4

№	X	Y	X2	Y2	XY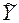
	3,21	5,10	10,30	26,01	16,37	4,65
	2,21	4,02	4,88	16,16	8,88	3,64
	2,11	3,22	4,45	10,37	6,79	3,54
	2,49	2,57	6,20	6,60	6,40	3,92
	3,19	3,62	10,18	13,10	11,55	4,63
	3,29	4,93	10,82	24,30	16,22	4,73
	4,41	6,53	19,45	42,64	28,80	5,86
	2,67	4,59	7,13	21,07	12,26	4,11
	0,75	2,82	0,56	7,95	2,12	2,16
	2,20	3,46	4,84	11,97	7,61	3,63
[ ]	26,53	40,86	78,82	180,17	117,00

Подставив полученные значения в формулу, получают

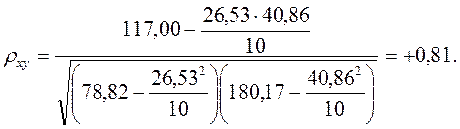
Для проверки значимости сравнивают вычисленное значение 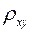с величиной 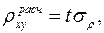где t – величина, выбираемая из таблиц нормального распределения по уровню значимости α = 0,05 (Приложение 3), а 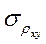- СКО величины ρ, вычисляемое по формуле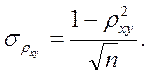

Сравнение 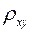с 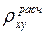приводит к выводу, что коэффициент корреляции значим.

Уравнение регрессии строят в виде

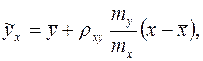
где

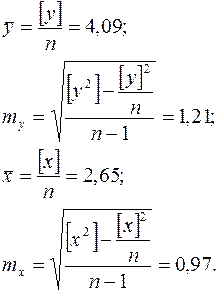
Подставляя вычисленные значения в формулу, получают

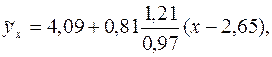
или окончательно

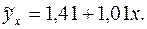
Значения 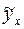для всех заданных значений х_i представлены в столбце 7 табл. 4.

По результатам расчетов строят график уравнения регрессии.

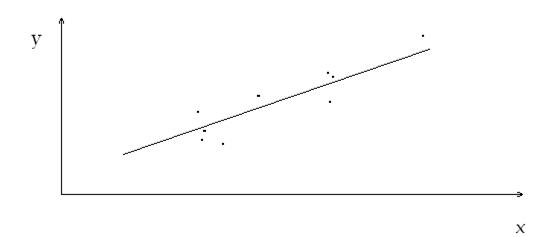
Рис. 1

Лабораторная работа № 3

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

по выполнению лабораторных работ по курсу

«Математической обработки результатов наблюдений»

Москва, 2017 г.

Лабораторная работа № 1

Статистическая обработка ряда наблюдений