Закон полного тока. магнитный поток
· Закон Ампера: сила 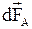 , действующая на элемент
, действующая на элемент 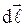 проводника с током
проводника с током 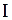 в магнитном поле
в магнитном поле 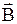 , равна
, равна
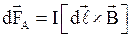 .
.
· Сила Лоренца: сила 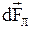 , действующая на заряд
, действующая на заряд 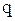 , движущийся со скоростью
, движущийся со скоростью 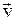 в магнитном поле
в магнитном поле 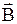 , равна
, равна
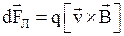 .
.
· Связь магнитной индукции и напряженности магнитного поля для изотропного магнетика 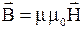 .
.
· Закон Био-Саварра-Лапласа 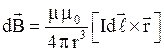 , где
, где 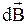 - магнитная индукция поля, создаваемого элементом проводника с током
- магнитная индукция поля, создаваемого элементом проводника с током 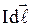 ;
; 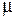 - магнитная проницаемость;
- магнитная проницаемость; 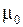 - магнитная постоянная;
- магнитная постоянная; 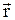 - радиус-вектор, проведенный от элемента тока до исследуемой точки.
- радиус-вектор, проведенный от элемента тока до исследуемой точки.
· Магнитное поле, создаваемого отрезком прямолинейного проводника с током:
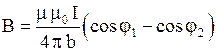 ,
,
где 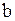 - расстояние от оси проводника;
- расстояние от оси проводника; 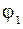 и
и 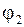 - углы между элементами тока, соответствующими началу и концу отрезка проводника с током, и радиусами-векторами, проведенными от этих элементов, до точки наблюдения.
- углы между элементами тока, соответствующими началу и концу отрезка проводника с током, и радиусами-векторами, проведенными от этих элементов, до точки наблюдения.
Для проводника с током конечной длины 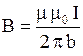 , так как
, так как 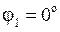 и
и 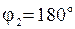 .
.
· Магнитное поле на оси кругового тока радиусом 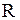
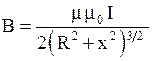 ,
,
где 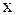 - расстояние от центра витка с током до точки наблюдения.
- расстояние от центра витка с током до точки наблюдения.
Соответственно поле в центре витка с током рассчитывают через формулу 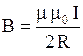 .
.
· Магнитное поле движущегося заряда 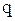 , движущегося в вакууме со скоростью
, движущегося в вакууме со скоростью 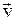
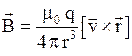 .
.
· Закон полного тока
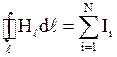 ,
,
где 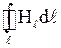 - циркуляция вектора
- циркуляция вектора 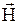 по замкнутому контуру;
по замкнутому контуру; 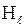 - проекция вектора напряженности
- проекция вектора напряженности 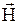 в данной точке контура на направление касательной к контуру в той же точке;
в данной точке контура на направление касательной к контуру в той же точке; 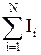 - сумма токов, охватываемых этим контуром.
- сумма токов, охватываемых этим контуром.
· Магнитное поле на средней линии тороида
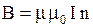 ,
,
где 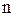 - число витков, приходящихся на единицу длины средней линии соленоида.
- число витков, приходящихся на единицу длины средней линии соленоида.
Магнитное поле бесконечно длинного соленоида вычисляют по этой же формуле; поле соленоида конечной длины вычисляют по формуле
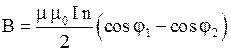 ,
,
где 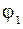 и
и 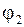 - углы между осью соленоида и радиус-векторами, проведенными из точки наблюдения к противоположным концам обмотки соленоида.
- углы между осью соленоида и радиус-векторами, проведенными из точки наблюдения к противоположным концам обмотки соленоида.
· Магнитный момент контура с током 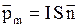 , где
, где 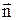 - единичный вектор, ортогональный плоскости контура и направленный по правилу буравчика;
- единичный вектор, ортогональный плоскости контура и направленный по правилу буравчика; 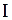 - сила тока в нем;
- сила тока в нем; 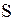 - площадь контура.
- площадь контура.
· Механический момент, действующий на контур с током, помещенный в однородное магнитное поле
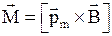 .
.
· Потенциальная энергия контура с током в магнитном поле
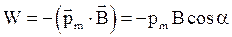 ,
,
где 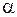 - угол между векторами
- угол между векторами 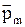 и
и 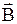 .
.
· Магнитный поток вектора через произвольную поверхность 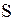 , помещенную в неоднородное поле,
, помещенную в неоднородное поле,
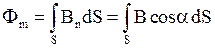 ,
,
где 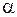 - угол между вектором магнитной индукции
- угол между вектором магнитной индукции 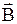 и нормалью
и нормалью 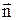 к элементу поверхности;
к элементу поверхности; 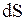 - площадь элемента поверхности;
- площадь элемента поверхности; 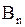 - проекция вектора напряженности на нормаль.
- проекция вектора напряженности на нормаль.
· Теорема Остроградского-Гаусса для магнитного поля
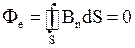 ,
,
где 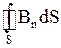 - поток вектора
- поток вектора 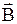 напряженности через замкнутую поверхность
напряженности через замкнутую поверхность 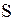 .
.
Работа по перемещению проводника с током в магнитном поле.
Электромагнитная индукция.
Энергия магнитного поля
· Работа по перемещению замкнутого контура с током в магнитном поле
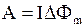 ,
,
где 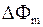 - изменение магнитного потока, пронизывающего поверхность, ограниченную контуром;
- изменение магнитного потока, пронизывающего поверхность, ограниченную контуром; 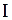 - сила тока в контуре.
- сила тока в контуре.
· Основной закон электромагнитной индукции 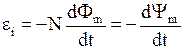 , где
, где 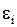 - электродвижущая сила индукции;
- электродвижущая сила индукции; 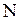 - число витков контура;
- число витков контура; 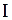 - сила тока в контуре.
- сила тока в контуре.
· Разность потенциалов 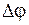 на концах проводника длиной
на концах проводника длиной 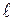 , движущегося со скоростью
, движущегося со скоростью 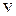 в однородном магнитном поле
в однородном магнитном поле 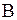
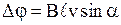 .
.
· Электродвижущая сила индукции 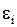 , возникающая в рамке, содержащей
, возникающая в рамке, содержащей 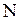 витков, площадью
витков, площадью 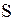 , при вращении рамки с угловой скоростью
, при вращении рамки с угловой скоростью 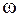 в однородном магнитном поле с индукцией
в однородном магнитном поле с индукцией 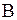
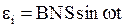 .
.
· ЭДС самоиндукции 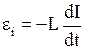 , где
, где 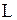 - индуктивность контура.
- индуктивность контура.
· Индуктивность соленоида 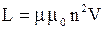 , где
, где 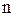 - число витков на единицу длины;
- число витков на единицу длины; 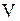 - объем соленоида.
- объем соленоида.
· Ток замыкания в цепи с индуктивностью 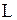 и активным сопротивлением
и активным сопротивлением 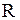
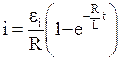 ,
,
где 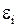 - ЭДС источника.
- ЭДС источника.
· Ток после размыкания цепи 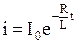 , где
, где 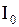 - сила тока в цепи при
- сила тока в цепи при  .
.
· Энергия магнитного поля, создаваемого током 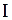 в замкнутом контуре с индуктивностью
в замкнутом контуре с индуктивностью 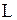
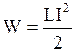 .
.
· Объемная плотность энергии магнитного поля
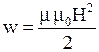 .
.
Магнитные свойства вещества
· Намагниченность диэлектрика 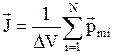 .
.
· Связь намагниченности в изотропном магнетике с напряженностью поля 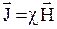 , где
, где 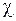 - магнитная восприимчивость.
- магнитная восприимчивость.
· Связь магнитной проницаемости 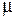 и магнитной восприимчивости
и магнитной восприимчивости 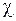 :
: 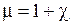 .
.
· Связь магнитной индукции, напряженности и намагниченности магнетика
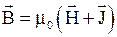 .
.
Система уравнений Максвелла
1. 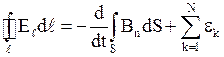 . 2.
. 2. 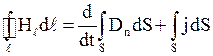 .
.
3. 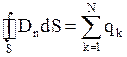 . 4.
. 4. 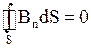 . 5.
. 5. 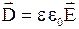 . 6.
. 6. 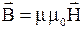 . 7.
. 7. 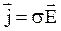 .
.
Глава 4. Колебания
Гармонические колебания
· Уравнение гармонических колебаний
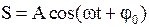 ,
,
где 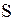 - смещение колеблющейся точки от положения равновесия;
- смещение колеблющейся точки от положения равновесия; 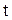 - время;
- время; 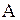 ,
, 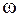 ,
, 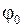 - соответственно амплитуда, угловая частота и начальная фаза колебаний;
- соответственно амплитуда, угловая частота и начальная фаза колебаний; 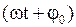 - фаза колебаний в момент времени
- фаза колебаний в момент времени 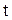 .
.
· Угловая частота колебаний 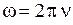 или
или 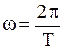 , где
, где 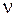 и
и 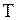 - частота и период колебаний.
- частота и период колебаний.
· Скорость точки, совершающей гармонические колебания
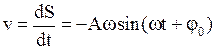 .
.
· Ускорение гармонических колебаний
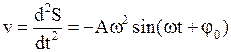 .
.
· Сложение однонаправленных колебаний одинаковой частоты:
- амплитуда результирующего колебания
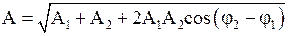 ,
,
где 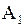 и
и 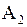 - амплитуды составляющих колебаний;
- амплитуды составляющих колебаний; 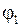 и
и 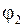 - их начальные фазы.
- их начальные фазы.
- начальная фаза результирующего колебания
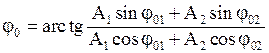 .
.
· Уравнение траектории точки при сложении двух взаимно перпендикулярных колебаний с амплитудами 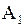 и
и 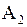 и начальными фазами
и начальными фазами 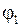 и
и 
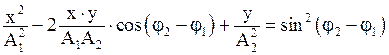 .
.
· Дифференциальное уравнение колебаний материальной точки
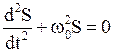 ,
,
где 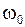 - собственная частота колебательной системы.
- собственная частота колебательной системы.
· Полная энергия механических гармонических колебаний 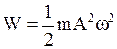 .
.
· Полная энергия электромагнитных колебаний 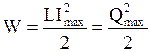 .
.
· Периоды колебаний гармонических колебательных систем:
- пружинный маятник: 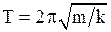 , где
, где 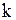 - коэффициент жесткости пружины;
- коэффициент жесткости пружины; 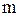 - масса тела;
- масса тела;
- математический маятник: 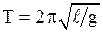 , где
, где 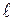 - длина нити маятника;
- длина нити маятника;
- физический маятник: 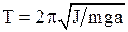 , где
, где 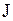 - момент инерции колеблющегося тела относительно оси колебаний;
- момент инерции колеблющегося тела относительно оси колебаний; 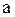 - расстояние от центра масс маятника до оси колебаний;
- расстояние от центра масс маятника до оси колебаний;
- электромагнитный колебательный контур: 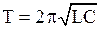 , где
, где 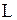 и
и 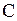 - соответственно индуктивность и емкость контура.
- соответственно индуктивность и емкость контура.
Затухающие колебания
· Дифференциальное уравнение затухающих колебаний
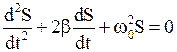 ,
,
где 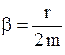 - для механических колебаний, где
- для механических колебаний, где 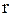 - коэффициент сопротивления;
- коэффициент сопротивления;
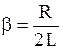 - для электромагнитных колебаний, где
- для электромагнитных колебаний, где 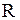 - активное сопротивление контура.
- активное сопротивление контура.
· Уравнение затухающих колебаний 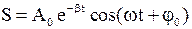 , где
, где 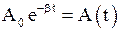 .
.
· Угловая частота затухающих колебаний 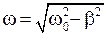 .
.
· Характеристики затухающих колебаний:
1) время релаксации 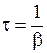 ;
;
2) логарифмический декремент затухания 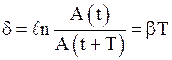 , где
, где 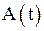 и
и 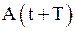 - амплитуды двух последовательных колебаний, отстоящих друг от друга по времени на период
- амплитуды двух последовательных колебаний, отстоящих друг от друга по времени на период 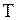 ;
;
3) добротность колебательной системы
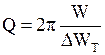 или
или 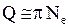 ,
,
где 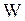 - энергия системы;
- энергия системы; 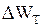 - убыль энергии системы за период;
- убыль энергии системы за период;
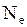 - число колебаний за время релаксации.
- число колебаний за время релаксации.
· Добротность колебательных систем:
- пружинный маятник: 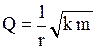 ;
;
- электромагнитный колебательный контур: 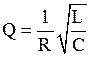 .
.
Вынужденные колебания
· Дифференциальное уравнение вынужденных механических колебаний
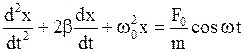 ,
,
где 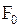 ,
, 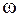 - амплитудное значение силы и круговая частота внешнего воздействия.
- амплитудное значение силы и круговая частота внешнего воздействия.
· Частное решение дифференциального уравнения вынужденных механических колебаний 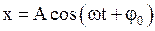 .
.
· Амплитуда вынужденных механических колебаний
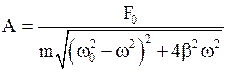 .
.
· Фаза вынужденных механических колебаний
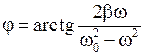 .
.
· Дифференциальное уравнение вынужденных электромагнитных колебаний
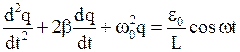 ,
,
где 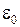 ,
, 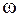 - амплитудное значение ЭДС и круговая частота внешнего источника.
- амплитудное значение ЭДС и круговая частота внешнего источника.
· Частное решение дифференциального уравнения вынужденных электромагнитных колебаний 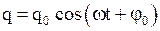 ,
,
где 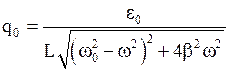 или
или 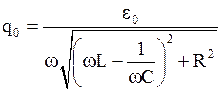 .
.
· Амплитуда вынужденных механических колебаний
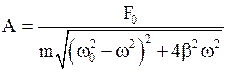 .
.
· Фаза вынужденных механических колебаний
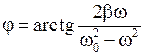 .
.
· Амплитудное значение тока при вынужденных электромагнитных колебаниях
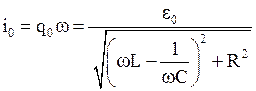 ,
,
где 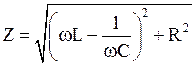 - полное колебание контура.
- полное колебание контура.
· Резонансная частота вынужденных колебаний 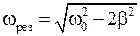 .
.
· Резонансная амплитуда вынужденных механических колебаний
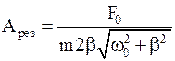 .
.
Глава 5. Волны
Волновые процессы
· Волновое уравнение для плоской бегущей гармонической волны, распространяющейся вдоль оси х:
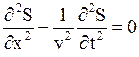 ,
,
· Уравнение плоской бегущей гармонической волны
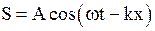 ,
,
где 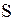 - смещение точек среды с координатой
- смещение точек среды с координатой 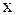 в момент времени
в момент времени 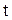 ;
; 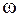 - угловая частота;
- угловая частота; 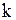 - волновое число;
- волновое число; 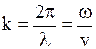 ;
; 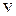 - скорость распространения волны в среде (фазовая скорость);
- скорость распространения волны в среде (фазовая скорость); 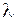 - длина волны;
- длина волны; 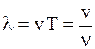 ;
; 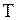 и
и 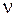 - период и частота колебаний.
- период и частота колебаний.
· Уравнение сферической волны
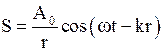 ,
,
где 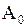 определяется свойствами источника;
определяется свойствами источника; 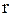 - расстояние от источника до точки наблюдения.
- расстояние от источника до точки наблюдения.
· Разность фаз колебаний двух точек среды, расстояние между которыми (разность хода) равно 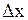 :
: 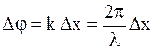 .
.
Упругие волны
· Фазовая скорость продольных волн в упругой среде:
- в твердых телах 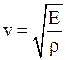 , где
, где 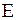 - модуль Юга;
- модуль Юга; 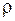 - плотность вещества;
- плотность вещества;
- в газах 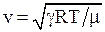 или
или 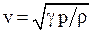 , где
, где 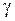 - показатель степени адиабаты;
- показатель степени адиабаты; 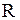 - универсальная газовая постоянная;
- универсальная газовая постоянная; 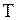 - термодинамическая температура;
- термодинамическая температура; 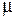 -молярная масса;
-молярная масса; 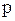 -давление газа.
-давление газа.
· Объемная плотность кинетической энергии в упругой волне
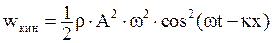 .
.
· Объемная плотность потенциальной энергии в упругой волне
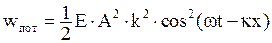 .
.
· Объемная плотность полной энергии
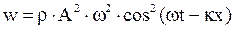 или
или 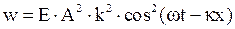 .
.
· Среднее за период значение объемной плотности энергии
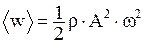 или
или 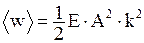 .
.
· Вектор плотности потока энергии (вектор Умова)
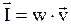 ,
,
где 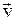 - вектор скорости волны.
- вектор скорости волны.
· Интенсивность звука 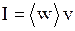 , где
, где 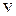 - скорость звука в среде.
- скорость звука в среде.
· Связь групповой и фазовой скорости
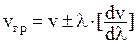 .
.
· Акустический эффект Доплера
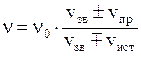 ,
,
где 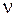 - частота звука, воспринимаемая движущимся приемником;
- частота звука, воспринимаемая движущимся приемником; 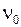 - частота звука, воспринимаемого приемником;
- частота звука, воспринимаемого приемником; 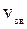 - скорость звука в среде;
- скорость звука в среде; 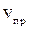 - скорость приемника относительно среды;
- скорость приемника относительно среды; 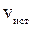 - скорость источника относительно среды.
- скорость источника относительно среды.
Электромагнитные волны
· Волновые уравнения для напряженностей электрического и магнитного полей плоской бегущей гармонической электромагнитной волны, распространяющейся вдоль оси х:
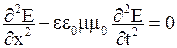 ,
,
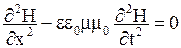 ,
,
где 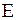 и
и 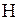 - напряженности электрического и магнитного полей в электромагнитной волне;
- напряженности электрического и магнитного полей в электромагнитной волне; 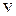 - фазовая скорость электромагнитной волны в среде с показателем преломления
- фазовая скорость электромагнитной волны в среде с показателем преломления 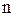 :
: 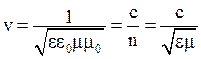 ;
; 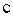 - скорость света в вакууме;
- скорость света в вакууме; 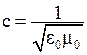 .
.
· Уравнения для напряженностей электрического и магнитного полей в плоской бегущей гармонической электромагнитной волне
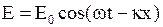 ,
,
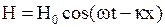 .
.
· Связь напряженностей электрического и магнитного полей в плоской бегущей гармонической электромагнитной волне
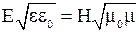 .
.
· Объемная плотность энергии электромагнитного поля
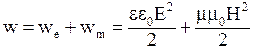 или
или
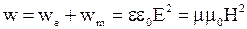 .
.
приемника относительно среды; 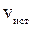 - скорость источника относительно среды.
- скорость источника относительно среды.
· Вектор плотности потока энергии электромагнитного поля
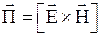 ,
,
где 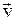 - вектор скорости волны.
- вектор скорости волны.
· Интенсивность электромагнитной волны 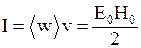 .
.
· Эффект Доплера для электромагнитных волн: если источник, испускающий волну частотой 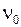 , движется со скоростью
, движется со скоростью 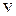 под углом
под углом 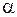 к направлению на наблюдателя, то воспринимаемая частота равна
к направлению на наблюдателя, то воспринимаемая частота равна
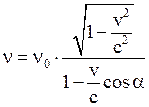 .
.
Глава 6. Волновые явления
Интерференция волн
· Оптический путь световой волны
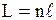 ,
,
где 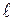 - геометрический путь световой волны в среде с показателем преломления
- геометрический путь световой волны в среде с показателем преломления 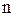 .
.
· Оптическая разность хода двух световых волн
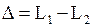 .
.
· Связь разности фаз с оптической разностью хода
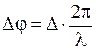 ,
,
где 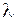 - длина волны в вакууме.
- длина волны в вакууме.
· Длина когерентности 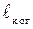 световой волны в вакууме
световой волны в вакууме
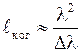 .
.
· Радиус когерентности волны, создаваемой протяженным источником на расстоянии 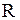 от него
от него
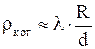 ,
,
где 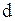 - линейный размер источника в плоскости, перпендикулярной направлению распространения волны.
- линейный размер источника в плоскости, перпендикулярной направлению распространения волны.
· Условия максимумов и минимумов интерференции двух волн, распространяющихся в одном направлении
- условие максимума 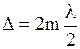
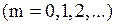 ;
;
- условие минимума 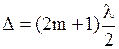
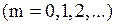 .
.
· Условия максимумов и минимумов интерференции световых волн, отраженных от верхней и нижней поверхностей тонкой плоскопараллельной пластины толщины 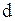 :
:
- условие максимума
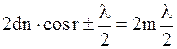
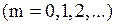 ,
,
- условие минимума
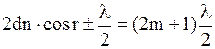 ,
, 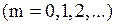
где 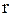 - угол преломления;
- угол преломления; 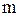 - номер максимума или минимума.
- номер максимума или минимума.
В проходящем свете условия максимумов и минимумов интерференции обратны условиям в отраженном свете (меняются местами).
· Радиусы светлых колец Ньютона в отраженном свете (или темных в проходящем)
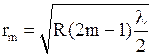
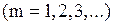 ,
,
где 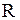 - радиус кривизны линзы, соприкасающейся с плоскопараллельной стеклянной пластинкой.
- радиус кривизны линзы, соприкасающейся с плоскопараллельной стеклянной пластинкой.
Радиусы темных колец в отраженном свете (или светлых в проходящем)
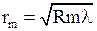
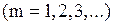 .
.
Дифракция волн
