Вынужденное излучение. Лазеры.
Отметим отличительное свойство квантовой системы – дискретность уровней энергии. В нормальных условиях ( при отсутствии внешних воздействий) большая часть электронов в атомах находятся на самом низком невозбужденном уровне  , остальные уровни
, остальные уровни  , соответствующие возбужденным состояниям, обладают минимальной заселенностью электронами или вообще свободны. Если атом находится в основном состоянии с
, соответствующие возбужденным состояниям, обладают минимальной заселенностью электронами или вообще свободны. Если атом находится в основном состоянии с  , то под действием внешнего излучения может осуществляться вынужденный переход в возбуждённое состояние с
, то под действием внешнего излучения может осуществляться вынужденный переход в возбуждённое состояние с 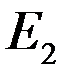 . Вероятность таких переходов пропорциональна плотности излучения, вызывающего эти переходы. Атом, находясь в возбужденном состоянии 2, может через некоторое время спонтанно (без внешних воздействий) перейти в состояние с низшей энергией, отдавая избыточную энергию в виде электромагнитного излучения, т.е. испуская фотон.
. Вероятность таких переходов пропорциональна плотности излучения, вызывающего эти переходы. Атом, находясь в возбужденном состоянии 2, может через некоторое время спонтанно (без внешних воздействий) перейти в состояние с низшей энергией, отдавая избыточную энергию в виде электромагнитного излучения, т.е. испуская фотон.
Процесс испускания фотона возбужденным атомом без каких-либо внешних воздействий называется спонтанным излучением. Чем больше вероятность спонтанных переходов, тем меньше среднее время жизни атома в возбужденном состоянии. Т.к. спонтанные переходы взаимно не связаны, то спонтанное излучение не когерентно. Если на атом, находящийся в возбужденном состоянии 2, действует внешнее излучение с частотой
 (1)
(1)
то возникает вынужденный (индуцированный) переход в основное состояние 1 с излучением фотона с той же частотой (1). Излучение, происходящее в результате внешнего облучения, называется вынужденным. В процесс вынужденного излучения вовлечены два фотона: первичный фотон, вызывающий испускание излучения возбужденным атомом, и вторичный фотон, испущенный атомом. Вторичные фотоны неотличимы от первичных. Эйнштейн и Дирак доказали тождественность вынужденного излучения вынуждающему излучению: они имеют одинаковую фазу, частоту, поляризацию и направление распространения. Вынужденное излучение строго когерентно с вынуждающим излучением.
Испущенные фотоны, двигаясь в одном направлении и, встречая другие возбужденные атомы, вызывают дальнейшие индуцированные переходы, и представляется, что число фотонов будет расти лавинообразно. Однако наряду с вынужденным излучением будет происходить поглощение. Поэтому для усиления падающего излучения необходимо, чтобы число фотонов в вынужденных излучениях (которое пропорционально заселенности возбужденных состояний) превышало число поглощенных фотонов. Если в системе атомы находятся в термодинамическом равновесии, поглощение будет преобладать над вынужденным излучением, т.е. падающее излучение при прохождении через вещество будет ослабляться.
Чтобы среда усиливала падающее на неё излучение необходимо создать неравновесное состояние системы, при котором число атомов в возбужденном состоянии больше, чем в основном. Такие состояния называются состояниями с инверсией заселённостей. Процесс создания неравновесного состояния вещества наз. накачкой. Накачку можно осуществить оптическими, электрическими и другими способами. В средах с инверсной заселённостью вынужденное излучение может превысить поглощение, т.е. падающее излучение при прохождении через среду будет усиливаться (такие среды наз. активными). Для этих сред в законе Бугера
 (2)
(2)
коэффициент 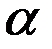 будет отрицательным.
будет отрицательным.
Лазеры – оптические квантовые генераторы.
Согласно законам квантовой механики, энергия электрона в атоме может иметь только определённый дискретный ряд значений
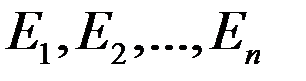 , называемых уровнями энергии. Эти значения различны для разных атомов. Набор дозволенных значений носит название энергетического спектра атома. В нормальных условиях (при отсутствии внешних воздействий) большая часть электронов в атомах находится на самом низком уровне
, называемых уровнями энергии. Эти значения различны для разных атомов. Набор дозволенных значений носит название энергетического спектра атома. В нормальных условиях (при отсутствии внешних воздействий) большая часть электронов в атомах находится на самом низком уровне 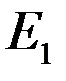 , остальные уровни называются возбужденными.
, остальные уровни называются возбужденными.
При переходе электрона с одного уровня энергии на другой атом может испускать или поглощать электромагнитные волны, частота которых определяется по формуле
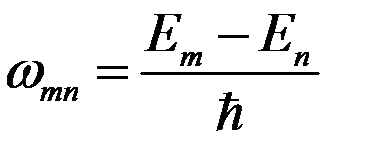 . (1)
. (1)
Возбужденный атом может отдать свою некоторую энергию, полученную, например, от внешнего источника, двумя различными способами.
Всякое возбужденное состояние атома неустойчиво, и всегда существует вероятность его самопроизвольного перехода в более низкое энергетическое состояние с испусканием фотона. Такой переход называется спонтанным. Он носит нерегулярный хаотический характер. Все обычные источники дают свет в результате спонтанного излучения. В рассмотренной двухуровневой схеме никакого усиления излучения добиться не удастся. Поглощённая энергия  выделяется в виде кванта с той же энергией и можно говорить о термодинамическом равновесии: процессы возбуждения атомов уравновешиваются обратными процессами испускания.
выделяется в виде кванта с той же энергией и можно говорить о термодинамическом равновесии: процессы возбуждения атомов уравновешиваются обратными процессами испускания.
Если подействовать на систему возбуждающим излучением с частотой, попадающей в резонанс с переходом между уровнями 1 и 3, то атомы будут поглощать это излучение и переходить с уровня 1 на уровень 3. Если интенсивность излучения достаточно велика, то число атомов, перешедших на уровень 3, может быть весьма значительным и мы, нарушив равновесное распределение населенностей уровней, увеличим населенность уровня 3 и уменьшим, следовательно, населённость уровня 1. С верхнего уровня 3 возможны переходы  и
и  . Переход
. Переход  не является излучательным: он ведет к заселению промежуточного уровня 2. Часть энергии электронов при этом переходе отдаётся веществу, нагревая его. Уровень 2 наз. метастабильным, и на нём в итоге окажется атомов больше, чем на первом. Поскольку атомы на уровень 2 поступают с основного уровня 1 через верхнее состояние 3, а обратно на основной уровень возвращаются с «большим запаздыванием» , то уровень 1 «обедняется».
не является излучательным: он ведет к заселению промежуточного уровня 2. Часть энергии электронов при этом переходе отдаётся веществу, нагревая его. Уровень 2 наз. метастабильным, и на нём в итоге окажется атомов больше, чем на первом. Поскольку атомы на уровень 2 поступают с основного уровня 1 через верхнее состояние 3, а обратно на основной уровень возвращаются с «большим запаздыванием» , то уровень 1 «обедняется».
В результате и возникает инверсия, т.е. обратное инверсное распределение населённостей уровней. Инверсия населённостей энергетических уровней создается интенсивным вспомогательным излучением, называемым излучением накачки и приводит в конечном итоге к индуцированному (вынужденному) размножению фотонов в инверсной среде.
Как во всяком генераторе, в лазере для получения режима генерации необходима обратная связь. В лазере обратная связь реализуется с помощью зеркал. Активная среда помещается между двумя зеркалами – плоскими или чаще вогнутыми. Одно зеркало делается сплошным, другое частично прозрачным. «Затравкой» для процесса генерации служит спонтанное излучение фотона. В результате движения этого фотона в среде он порождает лавину фотонов, летящих в том же направлении. Дойдя до полупрозрачного зеркала, лавина частично отразится, а частично пройдет сквозь зеркало наружу. После отражения от правого зеркала волна идет обратно, продолжая усиливаться. Далее она достигает левого зеркала, отражается и снова устремляется к правому зеркалу. Такие условия создаются только для осевых волн. Фотоны других направлений не способны забрать заметную часть запасённой в активной среде энергии. Выходящая из лазера волна является монохроматической, имеет почти плоский фронт, высокую степень пространственной и временной когерентности по всему сечению пучка.
Гипотеза де Бройля
Луи де Бройль в 1924 году выдвинул идею о том, что микрочастицы обладают волновыми свойствами. К тому времени в оптике уже сложилась парадоксальная, но подтвержденная опытом ситуация: в одних явлениях (интерференция, дифракция,…) свет ведёт себя как волны, другие явления (фотоэффект, эффект Комптона,…) показывают с неменьшей убедительностью, что он ведёт себя и как частицы. Таким образом, для света характерен корпускулярно-волновой дуализм. Де Бройль предположил, что корпускулярно-волновой дуализм распространяется и на обычное вещество. Гипотеза де Бройля была подтверждена экспериментально. Тонкий монохроматический пучок электронов пропускался через поликристаллическую фольгу толщиной 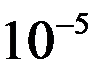 см. На фотопластинке, поставленной за фольгой, получалось центральное тёмное пятно, окруженное дифракционными кольцами. Получалась картина, такая же как и в случае дифракции рентгеновских лучей при пропускании через поликристаллическую фольгу.
см. На фотопластинке, поставленной за фольгой, получалось центральное тёмное пятно, окруженное дифракционными кольцами. Получалась картина, такая же как и в случае дифракции рентгеновских лучей при пропускании через поликристаллическую фольгу.
Пусть частица движется в свободном пространстве с постоянной скоростью. Де Бройль предположил, что с такой частицей связана плоская монохроматическая волна
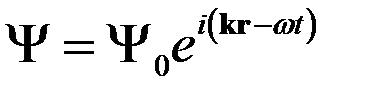 , (1)
, (1)
распространяющаяся в направлении скорости. При этом постулируются формулы
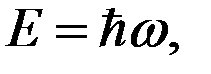 (2)
(2)
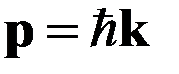 . (3)
. (3)
Они совпадают с соответствующими соотношениями для фотонов.
Уравнение Шредингера.
Найдем дифференциальное уравнение наименьшего порядка, которому удовлетворяет волна де Бройля . Имеем
 . (1)
. (1)
Далее находим

(2)
Отсюда получаем
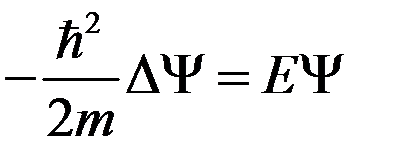 . (3)
. (3)
Далее имеем
 (4)
(4)
Отсюда находим
 . (5)
. (5)
Это и есть искомое дифференциальное уравнение, которому удовлетворяет волна де Бройля.
Обобщим уравнение (5) на случай движения в потенциальных силовых полях. Заметим, что  имеет размерность энергии. Значит одинаковую размерность имеют и величины
имеет размерность энергии. Значит одинаковую размерность имеют и величины  и
и  . Поэтому прибавление в правой части уравнения (5) слагаемого
. Поэтому прибавление в правой части уравнения (5) слагаемого  не меняет размерности этого уравнения. Можно предположить, что полученное таким путём уравнение
не меняет размерности этого уравнения. Можно предположить, что полученное таким путём уравнение
 . (6)
. (6)
будет правильно учитывать влияние потенциального силового поля на движение частицы.
Это уравнение называется уравнением Шредингера.
Уравнение Шредингера – существенно новый принцип. Его нельзя логически вывести из старых принципов, в которых он не содержится. Единственным доказательством уравнения Шредингера является только опыт – опытная проверка всех выводимых из него следствий. Такую проверку уравнение Шредингера выдержало.
Если потенциальная энергия не зависит от времени явно, решение уравнения Шредингера ищем в виде
 , (7)
, (7)
где  - полная энергия частицы. Подставляя (7) в (6) и сокращая на экспоненту, получим следующее дифференциальное уравнение
- полная энергия частицы. Подставляя (7) в (6) и сокращая на экспоненту, получим следующее дифференциальное уравнение
 . (8)
. (8)
Это уравнение не содержит времени и наз. уравнением Шредингера для стационарных состояний. Функция 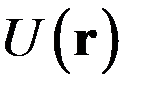 определяется классически, как если бы никакими волновыми свойствами частица не обладала.
определяется классически, как если бы никакими волновыми свойствами частица не обладала.
Уравнение Шредингера – первого порядка по времени. Отсюда следует, что заданием волновой функции  во всем пространстве в какой-либо момент времени однозначно определяется эта функция во всем пространстве во все последующие моменты времени. Данное утверждение не есть принцип причинности в квантовой механике, так как выражаемая им «причинность» относится к волновой функции
во всем пространстве в какой-либо момент времени однозначно определяется эта функция во всем пространстве во все последующие моменты времени. Данное утверждение не есть принцип причинности в квантовой механике, так как выражаемая им «причинность» относится к волновой функции  , а волновая функция связана с реально наблюдаемыми объектами вероятностными соотношениями. Поэтому квантовая механика является принципиально статистической теорией. Пси-функция не позволяет определить местоположение частицы в пространстве или траекторию, по которой движется частица. С помощью пси-функции можно лишь предсказать, с какой вероятностью частица может быть обнаружена в различных точках пространства. Квантовая механика вскрывает истинное поведение микрочастиц. Она лишь не определяет того, чего нет на самом деле. Применительно к микрочастицам понятия определённого местоположения и траектории вообще теряют смысл.
, а волновая функция связана с реально наблюдаемыми объектами вероятностными соотношениями. Поэтому квантовая механика является принципиально статистической теорией. Пси-функция не позволяет определить местоположение частицы в пространстве или траекторию, по которой движется частица. С помощью пси-функции можно лишь предсказать, с какой вероятностью частица может быть обнаружена в различных точках пространства. Квантовая механика вскрывает истинное поведение микрочастиц. Она лишь не определяет того, чего нет на самом деле. Применительно к микрочастицам понятия определённого местоположения и траектории вообще теряют смысл.
Уравнение Шредингера линейно и однородно относительно функции  .
.
Принцип суперпозиции сводится к двум утверждениям.
1. Если  и
и 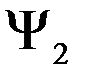 какие либо два решения уравнения Шредингера, то и всякая линейная их комбинация
какие либо два решения уравнения Шредингера, то и всякая линейная их комбинация  с постоянными (вообще говоря, комплексными) коэффициентами
с постоянными (вообще говоря, комплексными) коэффициентами 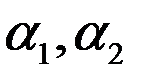 есть также решение того же уравнения.
есть также решение того же уравнения.
2. Если волновые функции  и
и 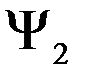 описывают какие-либо два состояния системы, то и линейная комбинация
описывают какие-либо два состояния системы, то и линейная комбинация  также описывает какое-то состояние той же системы.
также описывает какое-то состояние той же системы.
Согласно Борну квадрат модуля пси-функции определяет вероятность 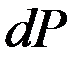 того, что частица будет обнаружена в пределах объема
того, что частица будет обнаружена в пределах объема 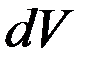 . Пси-функцию выбирают так, чтобы она удовлетворяла условию
. Пси-функцию выбирают так, чтобы она удовлетворяла условию
 . (9)
. (9)
Из формулы (9) заключаем, что квадрат модуля пси-функции дает плотность вероятности нахождения частицы в соответствующем месте пространства.
В соответствии со своим смыслом пси-функция должна быть однозначной, непрерывной и конечной (за исключением, быть может, особых точек). Кроме того, она должна иметь непрерывную и конечную производную. Совокупность перечисленных требований носит название стандартных условий.
Уравнению (8) можно придать вид
 . (10)
. (10)
Здесь
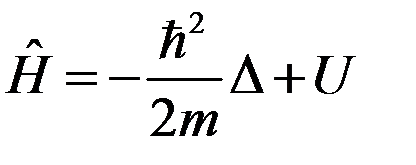 (11)
(11)
наз. оператором Гамильтона или гамильтонианом. Гамильтониан является оператором энергии 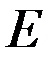 . Каждой динамической переменной
. Каждой динамической переменной  сопоставляется уравнение, аналогичное уравнению (10). Оно имеет вид
сопоставляется уравнение, аналогичное уравнению (10). Оно имеет вид
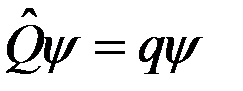 , (12)
, (12)
где  - оператор, сопоставляемый динамической переменной
- оператор, сопоставляемый динамической переменной 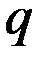 .
.
Квантование энергии
В уравнение Шредингера входит в качестве параметра полная энергия частицы 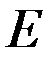 . В теории дифференциальных уравнений доказывается, что уравнения вида (9) из предыдущего раздела имеют решения, удовлетворяющие стандартным условиям, не при любых значениях параметра, а лишь при некоторых избранных значениях. Эти избранные значения называются собственными значениями соответствующей величины. Совокупность собственных значений наз. спектром величины. Спектры бывают дискретными и сплошными (непрерывными). Решения, соответствующие собственным значениям, наз. собственными функциями задачи. Квантование энергии получается из основных положений квантовой механики без каких-либо дополнительных предположений.
. В теории дифференциальных уравнений доказывается, что уравнения вида (9) из предыдущего раздела имеют решения, удовлетворяющие стандартным условиям, не при любых значениях параметра, а лишь при некоторых избранных значениях. Эти избранные значения называются собственными значениями соответствующей величины. Совокупность собственных значений наз. спектром величины. Спектры бывают дискретными и сплошными (непрерывными). Решения, соответствующие собственным значениям, наз. собственными функциями задачи. Квантование энергии получается из основных положений квантовой механики без каких-либо дополнительных предположений.
Рассмотрим простейший пример –энергию частицы в бесконечно глубокой одномерной потенциальной яме. Частица может двигаться только вдоль оси 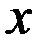 . Движение ограничено непроницаемыми стенками:
. Движение ограничено непроницаемыми стенками:  и
и 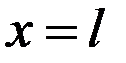 . Потенциальная энергия
. Потенциальная энергия  равна нулю при
равна нулю при 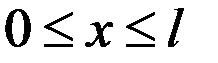 и обращается в
и обращается в  за пределами этой области. Вероятность обнаружить частицу за пределами потенциальной ямы равна нулю, а, следовательно, и функция
за пределами этой области. Вероятность обнаружить частицу за пределами потенциальной ямы равна нулю, а, следовательно, и функция 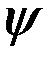 за пределами ямы равна нулю. Из условия непрерывности следует, что
за пределами ямы равна нулю. Из условия непрерывности следует, что  должна быть равна нулю и на границе ямы, т.е. должны выполняться граничные условия
должна быть равна нулю и на границе ямы, т.е. должны выполняться граничные условия
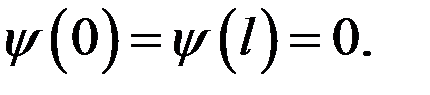 (1)
(1)
В области, где 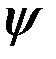 не равна тождественно нулю, уравнение Шредингера имеет вид
не равна тождественно нулю, уравнение Шредингера имеет вид
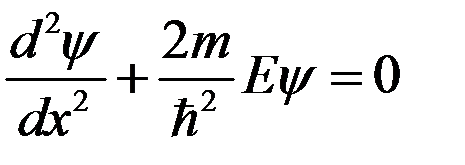 . (2)
. (2)
Или
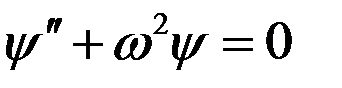 , (3)
, (3)
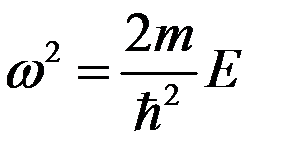 . (4)
. (4)
Решение имеет вид
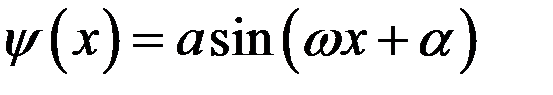 . (5)
. (5)
Далее получаем
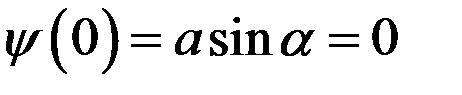 . (6)
. (6)
Следовательно, постоянная 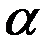 должна быть равна нулю. Далее, должно выполнять условие
должна быть равна нулю. Далее, должно выполнять условие
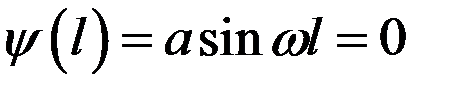 , (7)
, (7)
что возможно лишь в случае
 ,
, 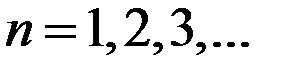 . (8)
. (8)
Случай 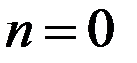 отпадает, поскольку при этом получается
отпадает, поскольку при этом получается  - частица нигде не находится. Далее имеем
- частица нигде не находится. Далее имеем
 . (9)
. (9)
Используя (4), находим энергию частицы
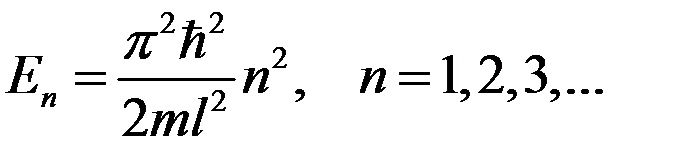 . (10)
. (10)
Спектр энергии оказался дискретным. Оценим расстояния между соседними уровнями. Разность энергий двух соседних уровней равна
 . (11)
. (11)
Если взять  порядка массы электрона
порядка массы электрона  при размере ямы
при размере ямы  порядка 10 см, то
порядка 10 см, то
 эрг
эрг  эВ. (12)
эВ. (12)
Густо расположенные энергетические уровни будут практически восприниматься как сплошной спектр энергии, так что хотя квантование энергии в принципе будет иметь место, но на характере движения электронов в этом случае сказываться не будет. Совсем иной результат получается для электрона , если область, в пределах которой он движется, будет порядка атомных размеров  . В этом случае
. В этом случае
 эрг
эрг 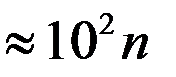 эВ,
эВ,
так что дискретность энергетических уровней будет весьма заметной. Собственные функции имеют вид

Например, в состоянии при  частица не может быть обнаружена в середине ямы и вместе с тем одинаково часто бывает как в левой, так и в
частица не может быть обнаружена в середине ямы и вместе с тем одинаково часто бывает как в левой, так и в
правой половине ямы. Такое поведение частицы несовместимо с представлением о траекториях. Согласно классическим представлениям все положения частицы в яме равновероятны.
