Функция Лагранжа и принцип наименьшего действия
Основное требование СТО – релятивистская ковариантность уравнений механики. Т.е. запись их в такой форме, чтобы они были справедливы в любой инерциальной форме отсчета. Этому требованию легко удовлетворить, если использовать принцип наименьшего действия. Формула для действия
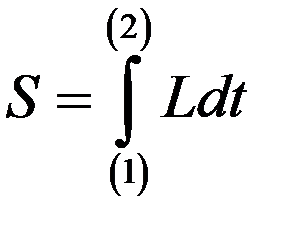 . (1)
. (1)
Более подробно:
Каждая механическая система характеризуется определённой функцией
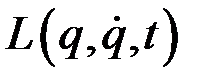 .
.
В точках 1 и 2 задаются координаты частицы и соответствующие моменты времени. Тогда между этими положениями система движется так, чтобы интеграл
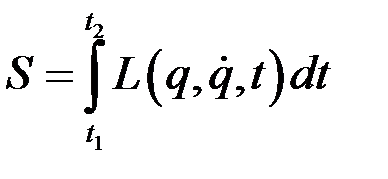 (1)
(1)
имел наименьшее возможное значение. Данный интеграл называется действием. Принцип наименьшего действия можно записать в виде
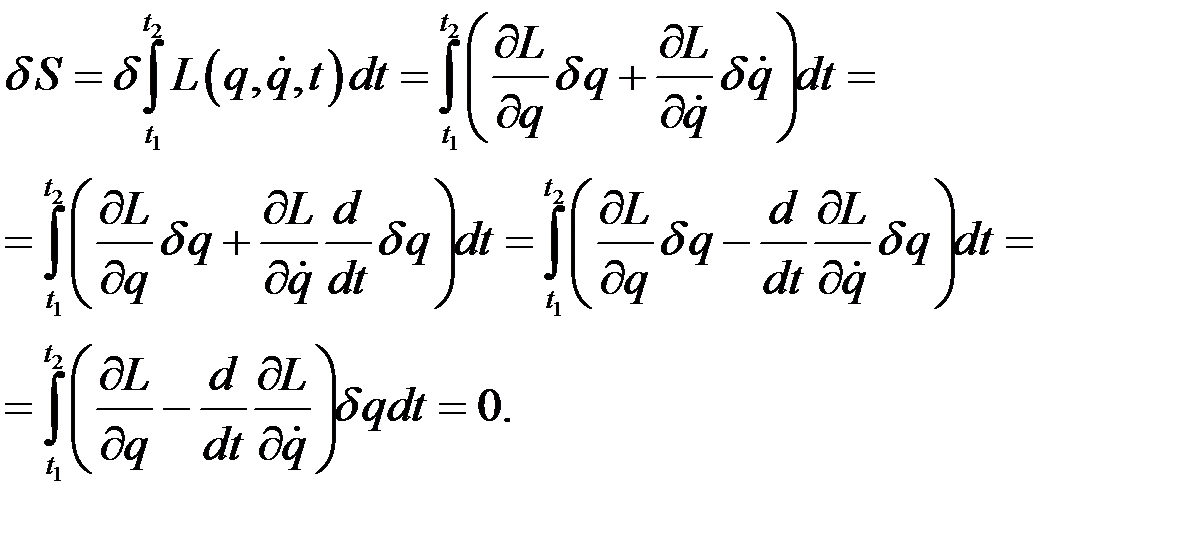 (2)
(2)
Интеграл должен быть равен нулю при произвольных значениях 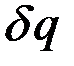 . Это возможно только в том случае, когда подынтегральное выражение тождественно обращается в нуль. Получаем уравнение
. Это возможно только в том случае, когда подынтегральное выражение тождественно обращается в нуль. Получаем уравнение
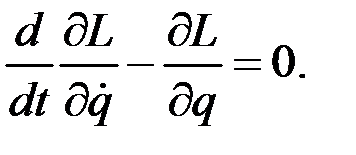 (3)
(3)
Это уравнение может быть записано в виде
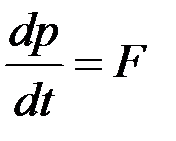 . (4)
. (4)
Величину
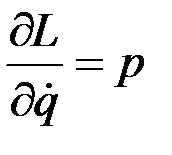 (5)
(5)
наз. обобщённым импульсом, а величину
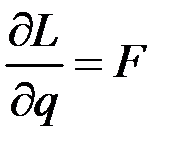 (6)
(6)
наз. обобщённой силой.
В частном случае свободной частицы в нерелятивистской механике
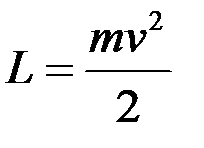 . (7)
. (7)
Интеграл (1) не должен зависеть от выбора той или иной инерциальной системы отсчета. Поэтому он должен быть взят от скаляра. Единственный скаляр для свободной частицы есть 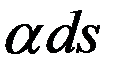 , где
, где 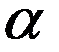 -постоянная инвариантная величина. Рассмотрим действие для релятивистской частицы
-постоянная инвариантная величина. Рассмотрим действие для релятивистской частицы
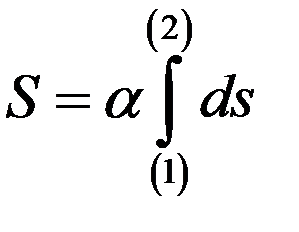 . (2)
. (2)
Приведем (2) к виду (1). Имеем
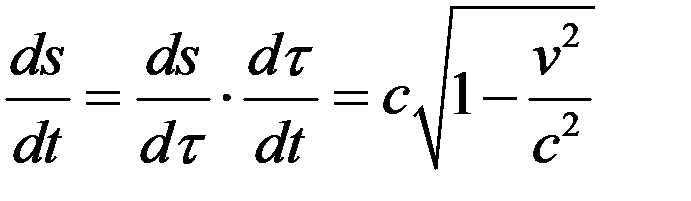 . (3)
. (3)
Поэтому
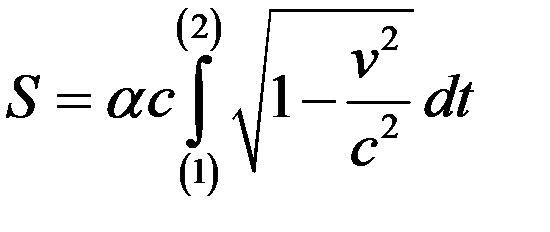 . (6)
. (6)
Отсюда следует
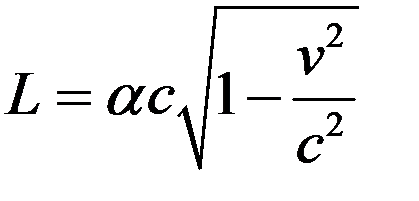 . (7)
. (7)
Значение 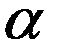 найдем из принципа соответствия. При
найдем из принципа соответствия. При 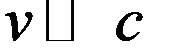 имеем
имеем
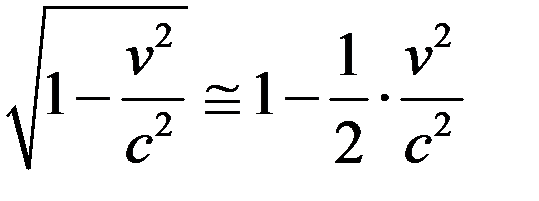 , (8)
, (8)
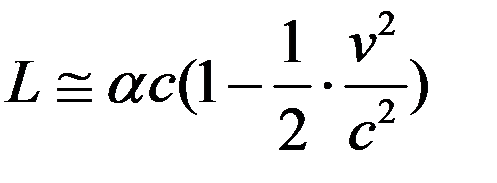 . (9)
. (9)
Так как в нерелятивистском случае
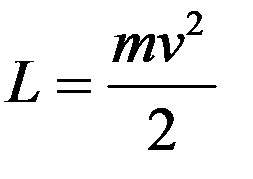 , (10)
, (10)
то следует положить
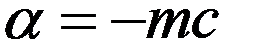 . (11)
. (11)
При этом в нерелятивистском случае
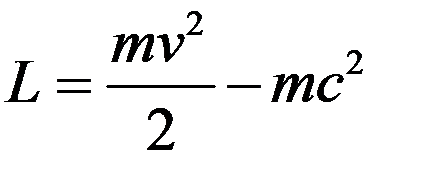 . (12)
. (12)
Отметим, что в нерелятивистском случае энергия и функция Лагранжа определяются с точностью до постоянного слагаемого.
Итак, в релятивистском случае
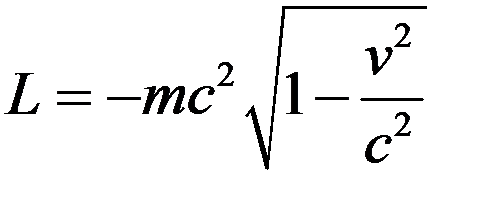 . (13)
. (13)
Некоторые сведения из математики
Частная производная
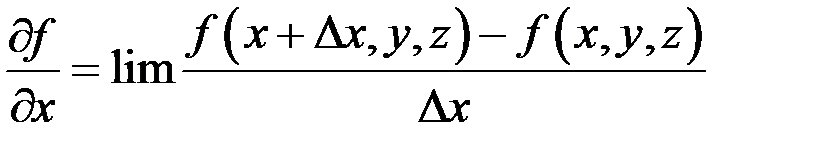 при
при 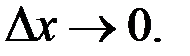
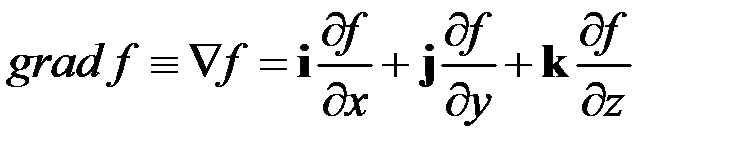 ,
,
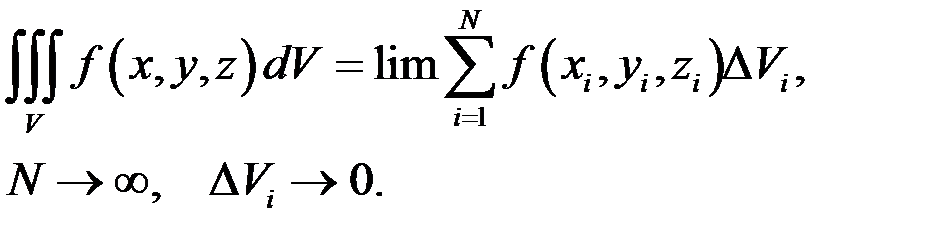
Поток вектора 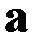 через поверхность
через поверхность
Поверхность разбивается на малые участки. Каждый такой участок можно считать плоским. К каждому участку проводится единичный вектор нормали 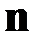 с направлением в соответствии с правилом правого буравчика. Определяется проекция вектора
с направлением в соответствии с правилом правого буравчика. Определяется проекция вектора 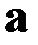 на направление
на направление
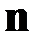 нормали. Далее эти проекции умножаются на соответствующие площади каждого малого участка и полученные результаты складываются. Получаем
нормали. Далее эти проекции умножаются на соответствующие площади каждого малого участка и полученные результаты складываются. Получаем
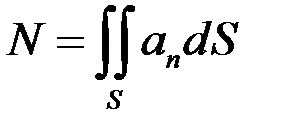 .
.
Если поверхность является замкнутой, то принято обозначение
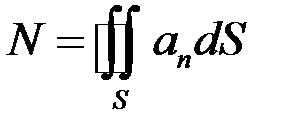 .
.
Определение дивергенции
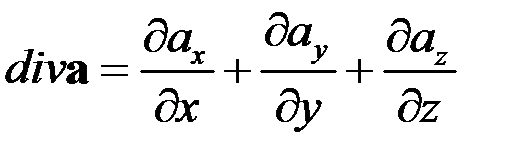 .
.
Определение ротора
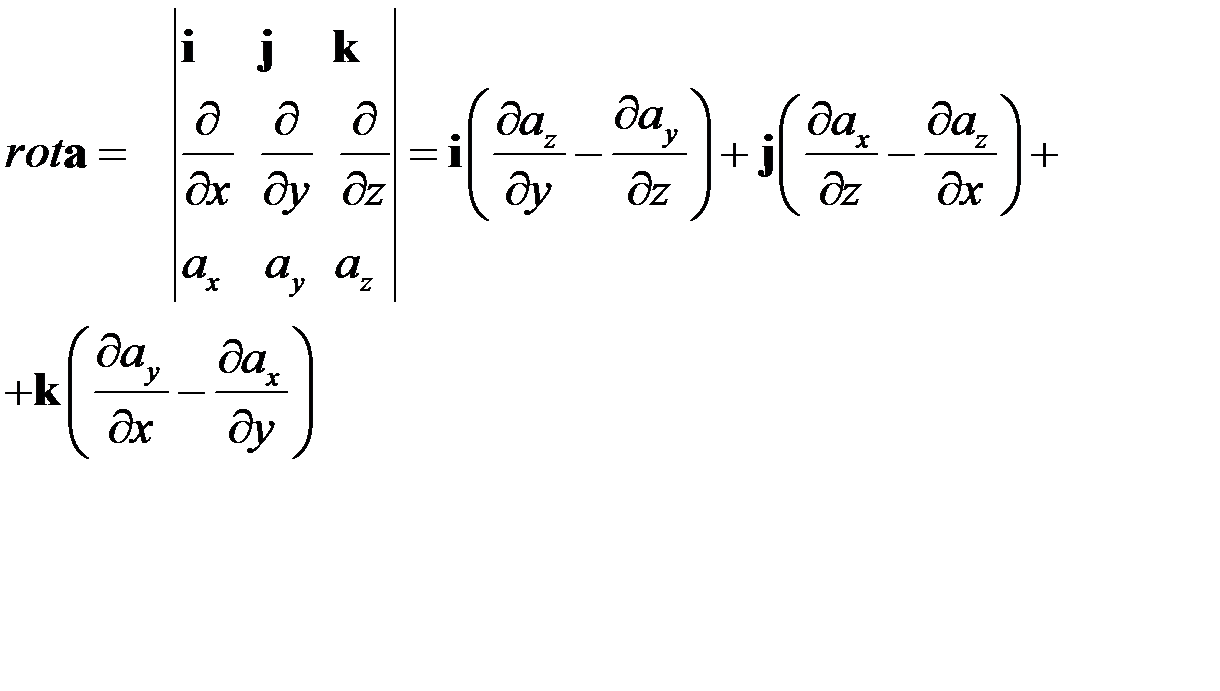
Теорема Гаусса-Остроградского
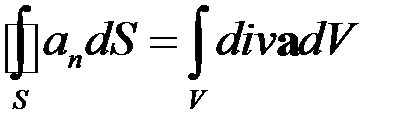
Теорема Стокса
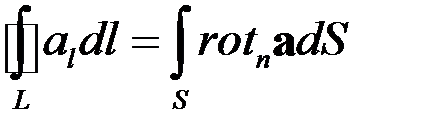
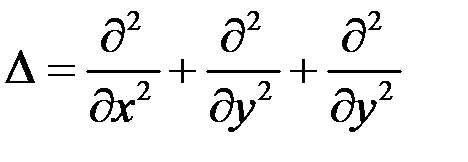
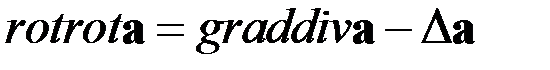
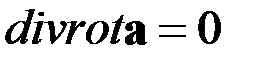
Энергия и импульс свободной частицы
Известно, что
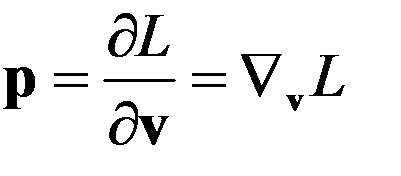 , (1)
, (1)
и
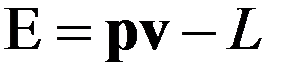 . (2)
. (2)
Поэтому
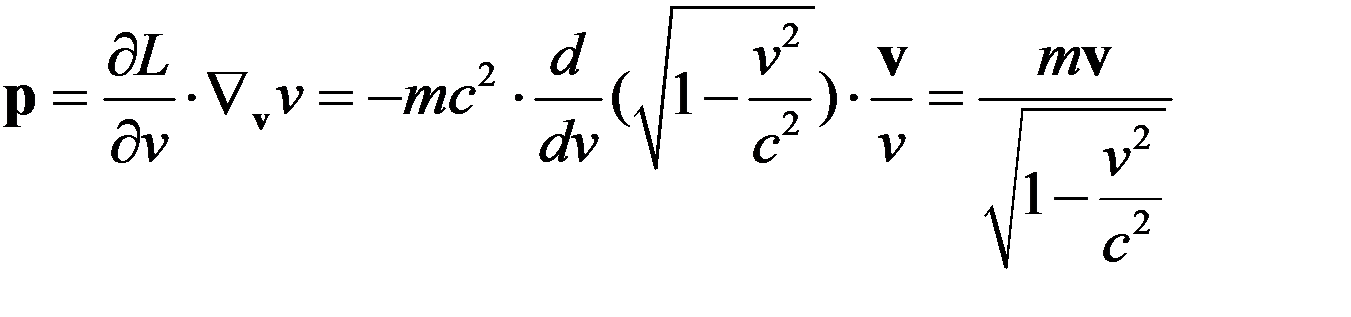 . (3)
. (3)
Далее имеем
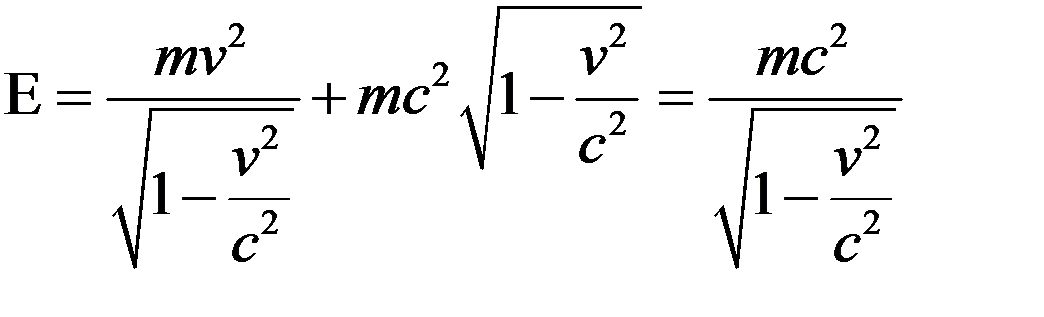 .
.
В нерелятивистском случае
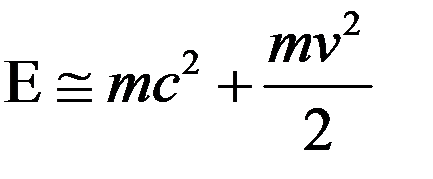 . (6).
. (6).
В процессах, в которых есть изменение массы, величину 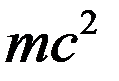 необходимо учитывать. Если масса изменяется, то соответствующее изменение энергии определяется по формуле
необходимо учитывать. Если масса изменяется, то соответствующее изменение энергии определяется по формуле
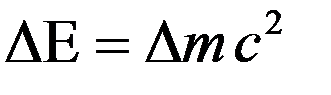 .
.
Были проведены опыты по превращению покоящегося электрона и позитрона в два 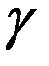 -кванта. Суммарная энергия
-кванта. Суммарная энергия 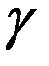 -квантов в точности равна сумме энергий покоя электрона и позитрона.
-квантов в точности равна сумме энергий покоя электрона и позитрона.
Уравнения Максвелла
Суммируя результаты теоретических и экспериментальных исследований, запишем систему четырех основных фундаментальных уравнений электродинамики в дифференциальной форме
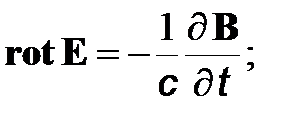 (2)
(2)
divB=0; (3)
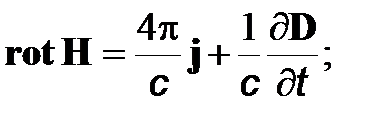 (4)
(4)
divD=4pr. (5)
Систему уравнений (2)–(5) называют системой уравнений Максвелла (уравнения (2), (3) составляют так называемую первую пару уравнений Максвелла, а уравнения (4), (5) - вторую пару уравнений Максвелла).
Отметим, что уравнение непрерывности , выражающее фундаментальный закон сохранения заряда, вытекает из второй пары уравнений Максвелла. Чтобы убедиться в этом, необходимо взять дивергенцию от обеих частей (4) и далее воспользоваться уравнением (5). Данное следствие уравнений Максвелла представляется вполне естественным, так как уравнение непрерывности непосредственно использовалось при поиске выражения для плотности тока смещения
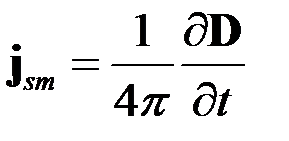 .
.
Дифференциальные уравнения (2)–(5) должны быть дополнены граничными условиями, которым должны удовлетворять величины E, H, D, B на границе раздела двух сред. Легко установить, что поверхностная плотность токов смещения всегда равна нулю. Поэтому совокупность граничных условий имеет вид
D2n–D1n=4ps; (6)
B2n=B1n; (7)
E2t=E1t; (8)
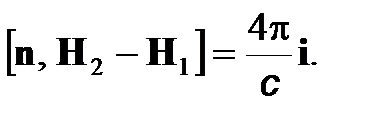 (9)
(9)
Здесь единичный вектор n, перпендикулярный к границе раздела, проведен из среды 1 в среду 2, s–поверхностная плотность заряда, i–поверхностная плотность тока проводимости.
Итак, источниками электрического поля являются либо электрические заряды, либо изменяющиеся во времени магнитные поля. Источниками же магнитного поля являются либо электрические токи (движущиеся заряды), либо переменные электрические поля.
Отсутствие симметрии уравнений относительно электрического и магнитного полей обусловлено предполагаемым отсутствием магнитных зарядов в природе ( неоднократные попытки обнаружить магнитные заряды до настоящего времени не увенчались успехом).
Интегральная форма уравнений Максвелла имеет вид
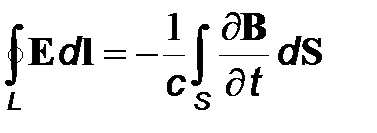 , (10)
, (10)
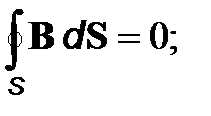 (11)
(11)
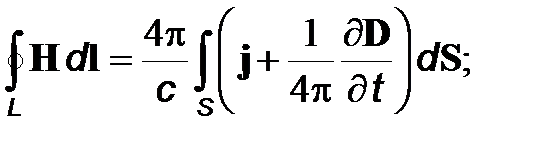 (12)
(12)
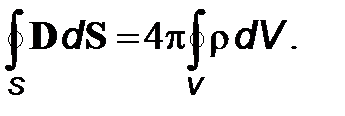 (13)
(13)
Отметим, что уравнение (12) представляет собой обобщение теоремы о циркуляции вектора напряженности магнитного поля. В уравнении (12) учтено, что магнитное поле создается как токами проводимости, так и токами смещения.
В интегральной форме уравнения Максвелла обладают наибольшей общностью, так как в этой форме уравнений не предполагается непрерывность входящих в уравнения величин. Эти уравнения выполняются и в тех случаях, когда существуют поверхности разрыва.
Система уравнений Максвелла не является полной. Например, система уравнений (2)-(5), записанная в координатной форме, содержит 8 скалярных уравнений, связывающих 16 величин. При использовании декартовой системы координат это следующие величины: Ex, Ey, Ez, Dx, Dy, Dz, Bx, By, Bz, Hx, Hy, Hz, jx, jy, jz,r.
Поэтому уравнения Максвелла необходимо дополнить так называемыми материальными уравнениями. Эти уравнения должны характеризовать свойства среды, в которой возбуждается электромагнитное поле. Необходимо сразу подчеркнуть, что одна и та же среда может характеризоваться различными материальными уравнениями в зависимости от величины параметров электромагнитного поля. Материальные уравнения должны быть получены, вообще говоря, на основе молекулярной теории среды. Возможен и феноменологический подход, опирающийся на обобщение опытных данных. В сложных случаях получение материальных уравнений может представлять собой серьезную современную научную проблему.
Как показывают, в частности, экспериментальные исследования, материальные уравнения наиболее просты в изотропных неферромагнитных и несегнетоэлектрических средах при условии незначительного изменения электромагнитного поля за характерные времена собственных внутримолекулярных колебаний и на протяжении межмолекулярных расстояний и при условии малой величины электромагнитного поля по сравнению с характерным собственным полем молекул среды (такие условия обычно выполняются при решении многих технических задач). Эти материальные уравнения имеют вид
D=eE, (14)
B=mH, (15)
j=lE. (16)
Здесь e, m, l - диэлектрическая проницаемость, магнитная проницаемость, электропроводность среды.
Теперь к основной системе уравнений Максвелла добавляется 9 скалярных материальных уравнений, и общее число уравнений становится равным 17. Некоторая математическая переопределенность общей системы уравнений обусловлена тем обстоятельством, что уравнение (3) при соответствующем выборе начального условия вытекает из уравнения (2). Действительно, возьмем дивергенцию от обеих частей уравнения (2). Тогда получим
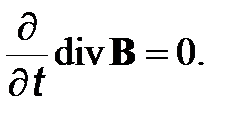 (17)
(17)
Уравнение (17) означает, что если divB=0 в начальный момент времени, то она будет равна нулю и в последующие моменты времени. Поэтому уравнение (3) с формальной точки зрения фактически лишь накладывает ограничение на вид начального условия для B.
Отметим, что в анизотропной среде, например, закон Ома принимает вид
ji=likEk. (18)
В формуле (18), как обычно, подразумевается суммирование по повторяющемуся индексу, lik–тензор электропроводности. В анизотропных средах и в сильных полях вместо (18) нередко используют следующее более общее уравнение:
ji=likEk+giknEkEn+ziknmEkEnEm. (19)
В курсе теоретической физики система уравнений Максвелла в вакууме формулируется как инвариантная система, служащая для определения четырехмерного тензора второго ранга–тензора электромагнитного поля. С помощью данного тензора можно описывать электромагнитное поле инвариантным способом (в смысле теории относительности). В рамках такого описания отчетливо проявляется следующее свойство: электрическое и магнитное поле являются составляющими единого электромагнитного поля. Выделить определенные электрическое и магнитное поле можно только в том случае, если выбрана инерциальная система отсчета. Можно находить инерциальные системы отсчета, в которых данное электромагнитное поле имеет наиболее простой вид. Например, в определенных случаях можно найти такую инерциальную систему отсчета, в которой в нуль обращается напряженность электрического поля, либо напряженность магнитного поля.
