Концепции биологических систем.

Термин «биосфера» введен в 1875 году австрийским геологом и па- леонтологом Э.Зюссом для обозначения сферы жизни на Земле. Пред- шествующие естествоиспытатели использовали понятия «картина при- роды» ,«пространство жизни» ,«живая оболочка Земли», схожие с поня- тием «биосфера» по содержанию.

По-разному трактовалась учеными роль живых организмов в био-

сфере: в основном отмечалась зависимость живых организмов от окру- жающей среды, от сил и веществ неживой природы; обратному же влиянию живых организмов на окружающую среду, на ее состав и свой- ства, как правило, не придавалось значения. ЖБ.Ламарк первым отметил огромную роль живых организмов в образовании земной коры, высказав мысль о том, что все вещества на Земле сформировались в результате деятельности живых организмов.

По современным представлениям биосфера являет собой единство живой и неживой природы, в котором существуют и взаимодействуют живые организмы с физическими, химическими, геологическими факто-

рами окружающей среды; между живой и неживой природой существу-

ют обратные связи, как положительные, так и отрицательные, которые влияют на состояние природных систем Земли. Положительные обрат-

ные связи играют важную роль при разрушении сложившихся связей в природных системах в процессе их эволюции и образовании новых свя- зей, определяющих новое состояние природных систем . Отрицательные

связи, напротив, способствуют устойчивости природных систем, обере- гая их от разрушения и восстанавливая прежние кондиции природных систем Земли. Именно благодаря отрицательным обратным связям при-

родные системы способны гасить антропогенное давление на окружаю-

щую среду и поддерживать системы в квазиустойчивом состоянии.

Тем

Влияние обратных связей в системах на характеристики сис-

Система без обратных связей

X (t) y(t)

k y(t)=kx(t)

где х(t)-воздействие на систему ;

у(t)-отклик ( реакция системы );

k-коэффициент передачи системы.

Если система линейна, то формы y(t) и x(t) одинаковы,- система функционирует как преобразователь воздействия без искажения его формы. При этом понятие формы может быть отнесено как к временной зависимости воздействия и отклика системы, так и к их законам распре- деления. В нелинейных системах формы y(t) и x(t) неодинаковы.

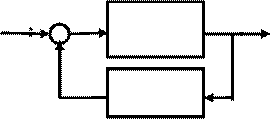
2. Система с положительной обратной связью ( ПОС ).

x(t) e(t) к y(t)

y(t)=k +x(t)

+

z(t) m

где х(t)-воздействие на систему- «входной сигнал » системы;

у(t)-отклик ( реакция системы )- «выходной сигнал» системы;

k -коэффициент передачи системы ( без обратной связи );

m-коэффициент обратной связи;

z(t)- отклик системы по каналу обратной связи- «сигнал обратной связи» системы;

k +-коэффициент передачи системы, охваченной положительной обратной связью .

Определим связь коэффициентов передачи в системе без обратной

связи и в системе с положительной обратной связью.

В системе c ПОС выполняются следующие соотношения:

e(t)=x(t)+z(t) ; y(t)=ke(t) ; z(t)=my(t),

откуда следует, что k +=

y(t )

x(t )

k

=1-mk.

Полученное соотношение показывает, что в системах с положительной обратной связью коэффициент передачи системы возрастает по сравне- нию с коэффициентом передачи системы без обратной связи. Кроме того

k + в предельном переходе ( m ®0

) обращается в

k. ( Принцип до-