Конструктивные особенности трансформатора
Раздел 3 - Трансформаторы
Однофазные трансформаторы
Конструкция и принцип действия трансформатора
Трансформатор – это статический электромагнитный аппарат, преобразующий электрическую энергию напряжения переменного тока с одними параметрами в электрическую энергию с другими параметрами (частота, напряжение, число фаз, форма напряжения и т.д.).
Принцип действия трансформатора основан на законе электромагнитной индукции. Конструкция однофазного трансформатора изображена на рисунке 3.1.
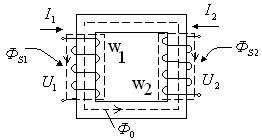
Рисунок 3.1 - Конструкция однофазного трансформатора
Здесь W1, W2 – первичная и вторичная обмотки соответственно; 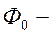 основной магнитный поток (магнитопровод трансформатора выполнен из ферромагнитного материала и предназначен для направления и концентрации основного магнитного потока);
основной магнитный поток (магнитопровод трансформатора выполнен из ферромагнитного материала и предназначен для направления и концентрации основного магнитного потока); 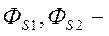 потоки рассеяния основного магнитного потока в обмотках первичной и вторичной цепей. Они зависят от сцепления обмоток (удаленности друг от друга), от расположения их на стержнях, а также от контура прохождения основного потока.
потоки рассеяния основного магнитного потока в обмотках первичной и вторичной цепей. Они зависят от сцепления обмоток (удаленности друг от друга), от расположения их на стержнях, а также от контура прохождения основного потока.
Рассмотрим работу трансформатора на “холостом" ходу. Представим принцип действия трансформатора в виде логической цепочки:
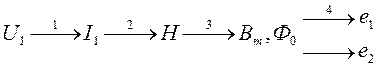
1. При подключении трансформатора к сети переменного тока возникает ток (по закону Ома), обратно пропорциональный входному сопротивлению трансформатора:
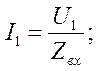
2. При протекании тока по обмотке трансформатора, намотанной на замкнутый магнитопровод, возникает напряженность магнитного поля (H):
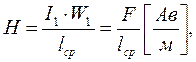
где F – магнитодвижущая сила (ампер 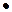 витки), lср – средняя линия магнитопровода, W1 – число витков в первичной обмотке.
витки), lср – средняя линия магнитопровода, W1 – число витков в первичной обмотке.
3. Под действием напряженности магнитного поля Н в магнитопроводе (сердечнике) трансформатора возникает основной магнитный поток Ф0, прямо пропорциональный индукции ( Вх) и сечению магнитопровода (Sмаг) как показано на рисунке 3.2.
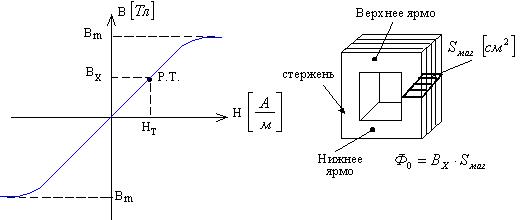
Рисунок 3.2 – Основная кривая намагничивания и сердечник трансформатора
Магнитная индукция Вх является рабочей точкой на основной кривой намагничивания и выбирается на линейном участке, чтобы при асимметричном намагничивании сердечника ( или постоянном подмагничивании ) не было захода рабочей точки в область насыщения.
4. При прохождении основного магнитного потока по сердечнику в первичной цепи возникает ЭДС самоиндукции, а во вторичной цепи ЭДС - взаимоиндукции, которые определяются по закону магнитодвижущих сил – закону Максвелла – Фарадея:
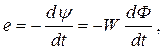
где e – изменение потокосцепления во времени.
Логическая цепочка работы трансформатора под нагрузкой
При подключении нагрузки во вторичной цепи начинает протекать ток 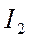 , при этом в сердечнике возникает размагничивающий магнитный поток Фр, противоположный по направлению основному потоку. Это приводит к уменьшению ЭДС в первичной цепи. В электромагнитной системе нарушается равновесие (
, при этом в сердечнике возникает размагничивающий магнитный поток Фр, противоположный по направлению основному потоку. Это приводит к уменьшению ЭДС в первичной цепи. В электромагнитной системе нарушается равновесие ( 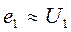 ), что приводит к возрастанию потребляемого тока из сети
), что приводит к возрастанию потребляемого тока из сети 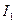 , т.е. к самобалансированию системы и поток
, т.е. к самобалансированию системы и поток 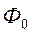 восстанавливается:
восстанавливается:
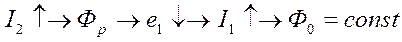 .
.
Отсюда следует уравнение магнитодвижущих сил (МДС):
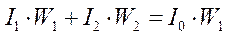 ,
,
где 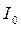 - ток цепи намагничивания (ток “холостого” хода).
- ток цепи намагничивания (ток “холостого” хода).
Уравнение ЭДС трансформатора
Рассмотрим уравнение ЭДС для низкочастотного трансформатора, в котором напряжение питания изменяется по синусоидальному закону:
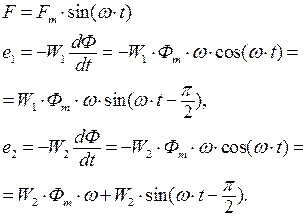 (3.1)
(3.1)
Из уравнения (3.1) следует, что ЭДС e1 , e2 отстают по фазе от потока Ф на угол π/2. Максимальное значение ЭДС
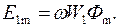
Разделив 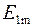 на
на 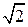 и, подставив
и, подставив 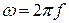 , получим действующее значение первичной ЭДС (В):
, получим действующее значение первичной ЭДС (В):
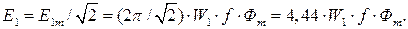 (3.2)
(3.2)
В современной электротехнике источником переменного напряжения часто являются инверторы напряжения (ИН). На рисунке 3.3 показаны две возможные формы напряжения в обмотках трансформатора инвертора.
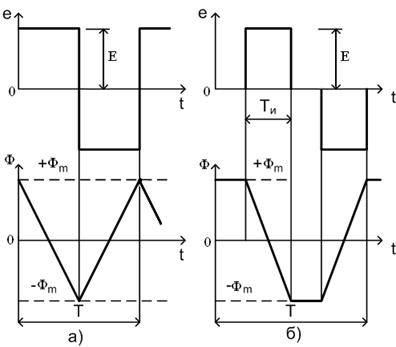
Рисунок 3.3 – Напряжение на обмотке трансформатора и магнитный поток
а) нерегулируемого инвертора; б) регулируемого инвертора
Получим уравнение ЭДС для трансформаторов при прямоугольной форме входного напряжения. Система уравнений для трансформатора имеет вид:
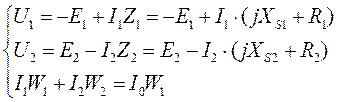 . (3.3)
. (3.3)
Пренебрегая сопротивлением первичной цепи трансформатора, на основании системы уравнений (3.3) можно записать u1≈ -e1.
Из уравнения электромагнитной индукции 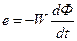 для е = Е (на интервале Δt = Tи) находим
для е = Е (на интервале Δt = Tи) находим
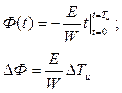
Так как уравнение Ф(t) описывает прямую линию, то в симметричном режиме перемагничивания можно принять
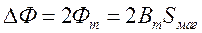
Из уравнений следует
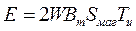
Введя обозначения Ти/Т = Кзи и 1/Т = f, получим выражение для уравнения ЭДС обмотки при прямоугольной форме напряжения:
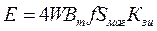
где Кзи = 0 ... 1,0 – коэффициент заполнения импульса в полупериоде. С изменением цифрового множителя в уравнении ЭДС несколько меняется и уравнение расчетной мощности трансформатора.
Приведем уравнение ЭДС к общему виду для любой формы напряжения. Для этого введем значение коэффициента формы KФ. Коэффициент формы определяет связь между действующим и средним значениями напряжений:
Кф=Е/Еср
Значения коэффициентов формы для распространенных электрических сигналов приведены в таблице ниже.
| Форма напряжения | 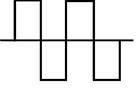 | 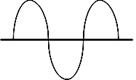 | 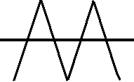 |
| Кф | 1,0 | 1,11 | 1,16 |
Для учета конструктивных особенностей сердечника трансформатора введем понятие коэффициента заполнения сердечника ферромагнитным материалом Kмаг, который учитывает процентное содержание магнитного материала в сечении сердечника Sмаг.ак = Sмаг. ×Kмаг . Под активной площадью сердечника Sмаг.ак понимается не геометрическая, а чистая площадь сечения магнитного материала. Для борьбы с вихревыми токами сердечник изготавливается из пластин или лент с лаковым покрытием, поэтому коэффициент Kмаг = 0,9…0,98.
Тогда выражение для ЭДС трансформатора принимает вид:
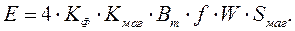
Из уравнения следует, что при неправильном проектировании трансформатора (выборе рабочей точки Вх на участке близком к области насыщения), например при понижении частоты напряжения питания или повышении уровня напряжения питания. происходит перегрев сердечника магнитопровода.
Опыт холостого хода
Условия проведения опыта: на вход подается номинальное напряжение U1ном, вторичная цепь размыкается.
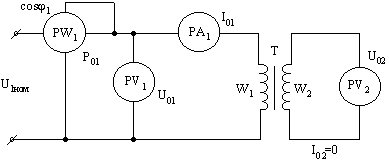
Измеряемыми параметрами являются номинальное напряжение вторичной цепи (U02) и первичной цепи (U01) (их называют напряжениями холостого хода), ток первичной цепи (I01 - ток холостого хода), активная мощность или потери в магнитопроводе (P01). Если устанавливаем измеритель коэффициента мощности, то активная мощность рассчитывается из соотношения:

В этом опыте рассчитываются - коэффициент трансформации (n) и значение процентного соотношения тока холостого хода к номинальному току первичной цепи
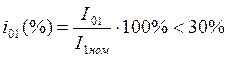
Это значение нормируется в процентах в зависимости от области использования трансформатора, его мощности и частоты.
Параметры схемы замещения поперечного плеча рассчитываются по соотношениям:
 ,
,  ,
, 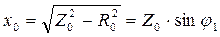 .
.
Если из опыта значение тока холостого хода получилось больше 30%, то значит завышено входное напряжение, или при проектировании завышена величина магнитной индукции. Для устранения этого потребуется измененить сечение магнитопровода или перемотать обмотки.
В опыте холостого хода схема замещения трансформатора принимает вид:

Так как параметры продольного плеча значительно меньше, чем параметры поперечного плеча схемы замещения и ток “холостого” хода значительно меньше номинального тока первичной цепи, то в схеме замещения трансформатора на “холостом” ходу пренебрегаем параметрами XS1 и R1.
Опыт короткого замыкания
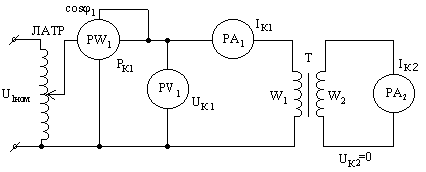
Опыт “короткого” замыкания проводится при пониженном напряжения питания, так как ток в обмотках трансформатора может превысить номинальные значения при повышении напряжения. Необходимо плавно увеличивать напряжение на выходе ЛАТРа до достижения номинальных токов в цепях. Измеряемыми параметрами являются: токи в цепях IК1, IK2 , напряжение короткого замыкания первичной цепи (UК1) и потери в обмотках. При измерении коэффициента мощности потери определяются из выражения:

Расчетными параметрами является процентное соотношение напряжения короткого замыкания по отношению к номинальному входному напряжению:

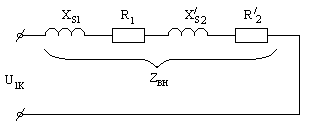
Внутреннее сопротивление трансформатора (сопротивление продольного плеча схема замещения) определяется из опыта “короткого” замыкания:
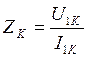 ,
,  ,
,  .
.
При переходе к реальным параметрам трансформатора принимается равенство:
 и
и  .
.
Схема замещения трансформатора в опыте “короткого” замыкания приводится к виду:
Трехфазные трансформаторы
Трехфазные сети широко распространены в энергетике и используются для производства и передачи электрической энергии. Трехфазные системы были разработаны русским электриком М.О.Доливо-Добровольским (1862 – 1919 гг.) и представляют собой систему из трёх источников переменного тока, ЭДС которых сдвинуты друг относительно друга на угол 120°.

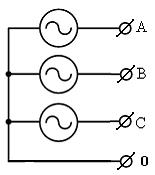
Это трёхпроводная и четырёхпроводная линии. Напряжение каждого генератора – фазное напряжение, а напряжение между фазами - линейное напряжение.
На рисунке изображены временные зависимости для фазных и линейных ЭДС трехфазной системы напряжений.

Трансформирование трехфазного тока можно осуществить тремя однофазными трансформаторами, соединенными в трансформаторную группу (так называемый групповой трансформатор) или трёхфазным трансформатором. Обмотки первичной и вторичной цепей соединяются одним из способов: ”звезда” - Y, “треугольник” - ∆ , “зигзаг” - Z.
Обмотки трехфазных трансформаторов принято соединять по следующим схемам: звезда; звезда с нулевым выводом; треугольник; зигзаг с нулевым выводом. Схемы соединения обмоток трансформатора обозначают дробью, в числителе которой указана схема соединения обмоток ВН (высшего напряжения), а в знаменателе — обмоток НН (низшего напряжения). Например, Y/Δ означает, что обмотки ВН соединены в звезду, а обмотки НН — в треугольник.
Соединение в зигзаг применяют только в трансформаторах специального назначения, например для выпрямителей. При соединении в зигзаг каждую фазу обмотки НН делят на две части, располагая их на разных стержнях. Указанные части обмоток соединяют так, чтобы конец одной части фазной обмотки был присоединен к концу другой части этой же обмотки, расположенной на другом стержне. Зигзаг называют равноплечным, если части обмоток, располагаемые на разных стержнях и соединяемые последовательно, одинаковы, и неравноплечными, если эти части неодинаковы. При соединении в зигзаг ЭДС отдельных частей обмоток геометрически вычитаются.
Выводы обмоток трансформаторов принято обозначать следующим образом: обмотки ВН — начало обмоток А, В, С, соответствующие концы X, Y, Z; обмотки НН — начала обмоток а, b, с, соответствующие концы х, у, z.
При соединении обмоток звездой линейное напряжение больше фазного в 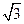 раз, а при соединении обмоток треугольником линейное напряжение равно фазному (Uл = Uф ).
раз, а при соединении обмоток треугольником линейное напряжение равно фазному (Uл = Uф ).
Отношение линейных напряжений трехфазного трансформатора определяется следующим образом:
| Схема соединения обмоток | Y/Y | Δ/Y | Δ/Δ | Y/Δ |
| Отношение линейных напряжений | w1/w2 | w1/( 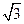 w2) w2) | w1/w2 | 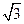 w1/w2 w1/w2 |
Видно, что отношение линейных напряжений в трехфазном трансформаторе определяется не только отношением чисел витков фазных обмоток, но и схемой их соединения.
Рассмотрим способ соединения “звезда”.
На рисунке изображена векторная диаграмма напряжений и условное обозначение схемы соединения обмоток трансформатора.
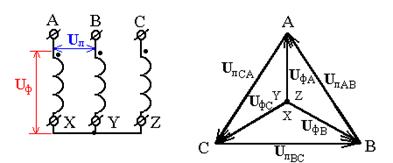
Точка на схеме трансформатора обозначает конец вектора ЭДС или начало обмотки.
При соединении звездой линейные (Iл) и фазные токи (Iф) одинаковы, потому что для тока, проходящего через фазную обмотку, нет иного пути, кроме линейного провода. Линейные напряжения (Uл) больше фазных (Uф) в 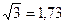 раза.
раза.

Соединение в звезду выполняется с нулевым выводом или без него, что является достоинством схемы соединения
Соединение в “треугольник”:
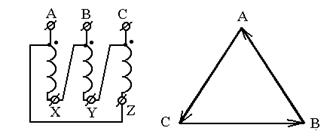
При соединении треугольником Uл = Uф, потому что каждые два линейных провода присоединены к началу и концу одной из фазных обмоток, а все фазные обмотки одинаковы. Линейные токи Iл = 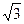 Iф.
Iф.
Мощность трёхфазной системы не зависит от схемы соединения (звездой или треугольником) и определяется выражениями:
Полная 
активная 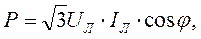 [Вт]
[Вт]
реактивная 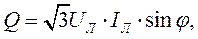 [ВАР]
[ВАР]
где j - угол сдвига фаз между напряжением и током.
Группы соединения обмоток трехфазного трансформатора
При определении группы соединения обмоток трансформатора пользуются циферблатом часов. Линейный вектор обмотки высшего напряжения (ВН) соответствует минутной стрелке циферблата часов и устанавливается на цифру 12, часовая стрелка соответствует линейному вектору ЭДС обмотки низкого напряжения (НН) и ее поворот по отношению к обмотке ВН определяет номер группы и угол поворота a = n*300, где n – группа.
Определим группу соединения обмоток трансформатора соединения “звезда-звезда”. Для построения диаграммы условно объединяют одноименные выводы обмоток первичной (С) и вторичной (с) цепей трансформатора. Из построения видно, что номер группы соединения равен
 |
n = 180°/30° = 6 .
Определим группу соединения обмоток трансформатора для соединения “звезда-треугольник”. Для построения диаграммы условно объединяем одноименные выводы обмоток первичной (а) и вторичной (А) цепей трансформатора. Из построения видно, что номер группы соединения равен n = j/30° =30°/30° = 1 .
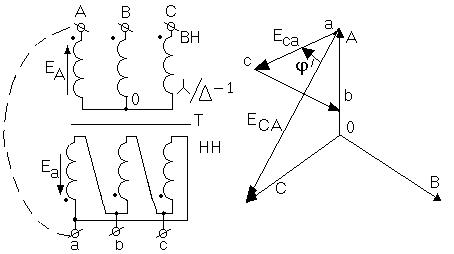
Соединение вторичных обмоток трансформатора в зигзаг
Соединение зигзагом применяют для того, чтобы нагрузку вторичных обмоток распределить более равномерно между фазами первичной сети, а также для расщепления фаз при создании многопульсных выпрямителей и в других случаях.
Для соединения зигзагом вторичная обмотка каждой фазы составляется из двух половин: одна половина расположена на одном стержне, другая – на другом. При таком соединении э.д.с. обмоток, расположенных на разных стержнях сдвинуты на угол 1200. .
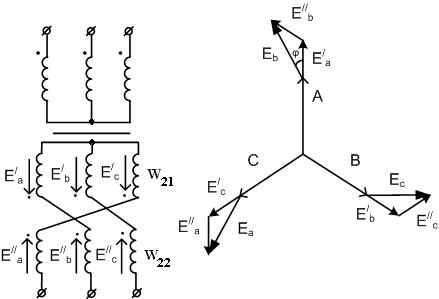
Угол поворота j вектора ЭДС вторичной цепи по отношению к первичной зависит от соотношения витков W21/W22.
Специальные трансформаторы
Трансформаторы напряжения
Измерительный трансформатор напряжения (ТН) применяется при измерениях в сетях переменного тока напряжением свыше 220 В. ТН представляет собой понижающий трансформатор с таким соотношением витков в первичной и вторичной обмотках, чтобы при номинальном первичном напряжении вторичное напряжение составляло 100В.
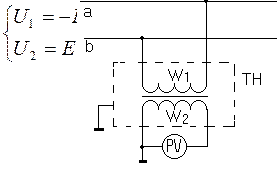 |
ТН работает в режиме, близком к режиму “холостого хода”, т.е. I2 = 0. Класс точности измерительной схемы зависит от выбора рабочей точки на петле гистерезиса (Bm=0,1….0,2 Тл , I1 » I0). Для его повышения увеличивают количество витков первичной цепи. Для обеспечения надежной работы ТН обязательно заземляется вторичная цепь и корпус трансформатора. Система уравнений для трансформатора следующая.
Так как U1 =-E1 , U2 = E2НОМ, то напряжение в первичной обмотке определяется выражением:
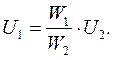
Трансформатор тока
Измерительный трансформатор тока (ТТ) применяется для включения амперметров и обмоток тока ваттметров, счетчиков энергии и фазометров в цепях переменного тока, чаще всего в сильноточных (с большим значением тока).
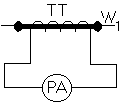 |
ТТ работает в режиме, близком к “короткому замыканию”. Первичная обмотка ТТ выполняется из провода большого сечения и включается в сеть последовательно (количество витков первичной цепи равно1). Вторичная обмотка - многовитковая.
Уравнение МДС имеет вид: I1W1 + I2W2 = I0W1;
Точность измерения тока определяется выбором точки на петле гистерезиса (Bm=0,1…0,2Тл, I0 =0). Количество витков во вторичной цепи подбирается таким , чтобы во вторичной цепи протекал ток 5 А, откуда
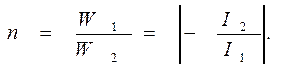
Данный трансформатор является опасным при эксплуатации, так как нельзя размыкать вторичную цепь под нагрузкой. При размыкании цепи произойдет рост потерь в магнитопроводе в квадратичной зависимости (В2), что может привести к пробою изоляции и обслуживающий персонал может попасть под высокое напряжение.
Раздел 3 - Трансформаторы
Однофазные трансформаторы
Конструкция и принцип действия трансформатора
Трансформатор – это статический электромагнитный аппарат, преобразующий электрическую энергию напряжения переменного тока с одними параметрами в электрическую энергию с другими параметрами (частота, напряжение, число фаз, форма напряжения и т.д.).
Принцип действия трансформатора основан на законе электромагнитной индукции. Конструкция однофазного трансформатора изображена на рисунке 3.1.

Рисунок 3.1 - Конструкция однофазного трансформатора
Здесь W1, W2 – первичная и вторичная обмотки соответственно; 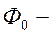 основной магнитный поток (магнитопровод трансформатора выполнен из ферромагнитного материала и предназначен для направления и концентрации основного магнитного потока);
основной магнитный поток (магнитопровод трансформатора выполнен из ферромагнитного материала и предназначен для направления и концентрации основного магнитного потока); 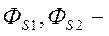 потоки рассеяния основного магнитного потока в обмотках первичной и вторичной цепей. Они зависят от сцепления обмоток (удаленности друг от друга), от расположения их на стержнях, а также от контура прохождения основного потока.
потоки рассеяния основного магнитного потока в обмотках первичной и вторичной цепей. Они зависят от сцепления обмоток (удаленности друг от друга), от расположения их на стержнях, а также от контура прохождения основного потока.
Рассмотрим работу трансформатора на “холостом" ходу. Представим принцип действия трансформатора в виде логической цепочки:
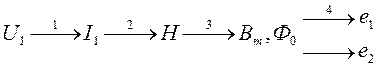
1. При подключении трансформатора к сети переменного тока возникает ток (по закону Ома), обратно пропорциональный входному сопротивлению трансформатора:
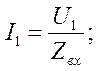
2. При протекании тока по обмотке трансформатора, намотанной на замкнутый магнитопровод, возникает напряженность магнитного поля (H):
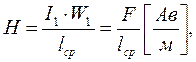
где F – магнитодвижущая сила (ампер 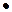 витки), lср – средняя линия магнитопровода, W1 – число витков в первичной обмотке.
витки), lср – средняя линия магнитопровода, W1 – число витков в первичной обмотке.
3. Под действием напряженности магнитного поля Н в магнитопроводе (сердечнике) трансформатора возникает основной магнитный поток Ф0, прямо пропорциональный индукции ( Вх) и сечению магнитопровода (Sмаг) как показано на рисунке 3.2.

Рисунок 3.2 – Основная кривая намагничивания и сердечник трансформатора
Магнитная индукция Вх является рабочей точкой на основной кривой намагничивания и выбирается на линейном участке, чтобы при асимметричном намагничивании сердечника ( или постоянном подмагничивании ) не было захода рабочей точки в область насыщения.
4. При прохождении основного магнитного потока по сердечнику в первичной цепи возникает ЭДС самоиндукции, а во вторичной цепи ЭДС - взаимоиндукции, которые определяются по закону магнитодвижущих сил – закону Максвелла – Фарадея:
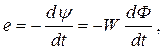
где e – изменение потокосцепления во времени.
Логическая цепочка работы трансформатора под нагрузкой
При подключении нагрузки во вторичной цепи начинает протекать ток 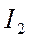 , при этом в сердечнике возникает размагничивающий магнитный поток Фр, противоположный по направлению основному потоку. Это приводит к уменьшению ЭДС в первичной цепи. В электромагнитной системе нарушается равновесие (
, при этом в сердечнике возникает размагничивающий магнитный поток Фр, противоположный по направлению основному потоку. Это приводит к уменьшению ЭДС в первичной цепи. В электромагнитной системе нарушается равновесие ( 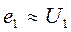 ), что приводит к возрастанию потребляемого тока из сети
), что приводит к возрастанию потребляемого тока из сети 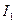 , т.е. к самобалансированию системы и поток
, т.е. к самобалансированию системы и поток 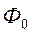 восстанавливается:
восстанавливается:
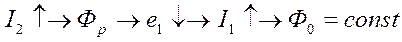 .
.
Отсюда следует уравнение магнитодвижущих сил (МДС):
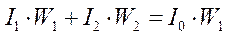 ,
,
где 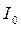 - ток цепи намагничивания (ток “холостого” хода).
- ток цепи намагничивания (ток “холостого” хода).
Уравнение ЭДС трансформатора
Рассмотрим уравнение ЭДС для низкочастотного трансформатора, в котором напряжение питания изменяется по синусоидальному закону:
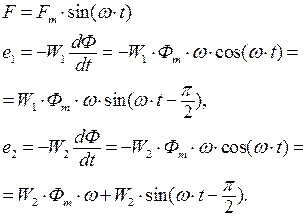 (3.1)
(3.1)
Из уравнения (3.1) следует, что ЭДС e1 , e2 отстают по фазе от потока Ф на угол π/2. Максимальное значение ЭДС
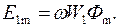
Разделив 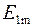 на
на 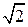 и, подставив
и, подставив 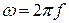 , получим действующее значение первичной ЭДС (В):
, получим действующее значение первичной ЭДС (В):
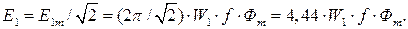 (3.2)
(3.2)
В современной электротехнике источником переменного напряжения часто являются инверторы напряжения (ИН). На рисунке 3.3 показаны две возможные формы напряжения в обмотках трансформатора инвертора.

Рисунок 3.3 – Напряжение на обмотке трансформатора и магнитный поток
а) нерегулируемого инвертора; б) регулируемого инвертора
Получим уравнение ЭДС для трансформаторов при прямоугольной форме входного напряжения. Система уравнений для трансформатора имеет вид:
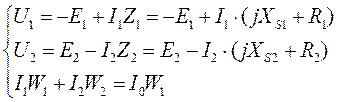 . (3.3)
. (3.3)
Пренебрегая сопротивлением первичной цепи трансформатора, на основании системы уравнений (3.3) можно записать u1≈ -e1.
Из уравнения электромагнитной индукции 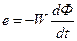 для е = Е (на интервале Δt = Tи) находим
для е = Е (на интервале Δt = Tи) находим
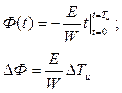
Так как уравнение Ф(t) описывает прямую линию, то в симметричном режиме перемагничивания можно принять
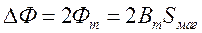
Из уравнений следует
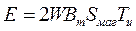
Введя обозначения Ти/Т = Кзи и 1/Т = f, получим выражение для уравнения ЭДС обмотки при прямоугольной форме напряжения:
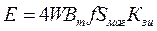
где Кзи = 0 ... 1,0 – коэффициент заполнения импульса в полупериоде. С изменением цифрового множителя в уравнении ЭДС несколько меняется и уравнение расчетной мощности трансформатора.
Приведем уравнение ЭДС к общему виду для любой формы напряжения. Для этого введем значение коэффициента формы KФ. Коэффициент формы определяет связь между действующим и средним значениями напряжений:
Кф=Е/Еср
Значения коэффициентов формы для распространенных электрических сигналов приведены в таблице ниже.
| Форма напряжения |  |  |  |
| Кф | 1,0 | 1,11 | 1,16 |
Для учета конструктивных особенностей сердечника трансформатора введем понятие коэффициента заполнения сердечника ферромагнитным материалом Kмаг, который учитывает процентное содержание магнитного материала в сечении сердечника Sмаг.ак = Sмаг. ×Kмаг . Под активной площадью сердечника Sмаг.ак понимается не геометрическая, а чистая площадь сечения магнитного материала. Для борьбы с вихревыми токами сердечник изготавливается из пластин или лент с лаковым покрытием, поэтому коэффициент Kмаг = 0,9…0,98.
Тогда выражение для ЭДС трансформатора принимает вид:
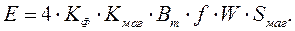
Из уравнения следует, что при неправильном проектировании трансформатора (выборе рабочей точки Вх на участке близком к области насыщения), например при понижении частоты напряжения питания или повышении уровня напряжения питания. происходит перегрев сердечника магнитопровода.
Конструктивные особенности трансформатора
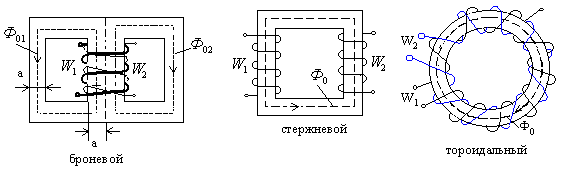
Однофазные силовые трансформаторы классифицируются по типу магнитопровода. Они делятся на броневые, стержневые и тороидальные.
Броневые сердечники используются при мощности менее 150В×А и частоте до 8 кГц, стрежневые - при мощности от 150 до 800 [В×А] и частоте до 8 кГц, тороидальные – при мощности до 250 [В×А] и частоте свыше 8 кГц.
В броневом сердечнике трансформатора основной магнитный поток раздваивается, что приводит к увеличению потока рассеяния. Расположение обмоток на одном (среднем) стержне трансформатора защищает обмотки от механических воздействий и электромагнитных помех. Такая конструкция обладает наибольшим рассеиванием основного потока ( 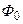 ), поэтому используется при малых мощностях.
), поэтому используется при малых мощностях.
В стержневом сердечнике трансформатора для улучшения сцепления обмоток первичную и вторичную обмотки разводят по двум стержням и при намотке чередуют послойно. В такой конструкции поток рассеяния меньше, чем в броневом трансформаторе.
Тороидальная конструкция сердечника трансформатора обладает наименьшим потоком рассеяния, благодаря круговому движению силовой линии основного магнитного потока Ф0 и хорошему сцеплению обмоток (из- за намотки по всему тороиду). Ограничение по мощности связано с плохим охлаждением сердечника и технологическими трудностями изготовления. Поперечное сечение тороида и стержней приближают к округлой форме, что позволяет экономить материал сердечника.
Сердечники магнитопроводов изготавливаются в виде лент, пластин или прессуют из ферромагнитного порошка с добавлением кремния. Низкочастотные трансформаторы выполняются из холоднокатанной (анизотропной или изотропной) стали, а также горячекатаной стали. 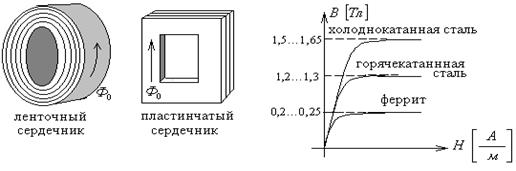
Основные виды магнитопроводов представлены в таблице.
| Внешний вид магнитопровода | Название | Шифр изделия | Основные размеры |
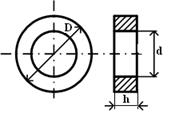 | Кольцевой сердечник | К | D*d*h |
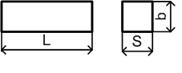 | Стержень прямоугольного сечения | С | b*s*L |
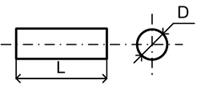 | Стержень круглого сечения | С | D*L |
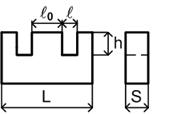 | Ш-образный сердечник | Ш | l0*S |
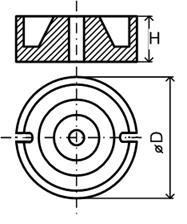 | Чашка броневого сердечника | Б | D |
Для улучшения магнитной связи между обмотками служит стальной магнитопровод. собранный из пластин специальной электротехнической стали марок 1511, 1512, 3411, 3412, 3413 и др. В этом обозначении первая цифра показывает класс стали по структурному состоянию и виду проката: 1 — горячекатанная, изотропная, 2 — холоднокатанная изотропная, 3 — холоднокатанчая анизотропная. Вторая цифра показывает процентное содержание кремния, присадка которого делает сталь более хрупкой и увеличивает электрическое сопротивление. Третья цифра указывает удельные потери (Вт/кг). Четвертая цифра — порядковый номер разработки. Холоднокатанная сталь обладает высокой магнитной проницаемостью и малыми удельными потерями, но является дорогостоящим материалом. В анизотропной холоднокатанной стали направление проката диктует направление силовой линии магнитного потока ( 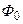 ) потому, что в перпендикулярном направлении ухудшаются магнитные свойства стали. Горячекатанная сталь более экономична, но имеет более высокие удельные потери и низкую магнитную проницаемость (mд).
) потому, что в перпендикулярном направлении ухудшаются магнитные свойства стали. Горячекатанная сталь более экономична, но имеет более высокие удельные потери и низкую магнитную проницаемость (mд).
В высокочастотных трансформаторах в качестве материала сердечников используют: феррит, пермаллой и альсифер. Альсифер(магнитодиэлектрик) используется для дросселей сглаживающих фильтров, т.к. имеется запас по намагниченности, пермаллой механически непрочен и дорог в изготовлении. Феррит обладает широким диапазоном рабочих частот, поэтому широко используется в импульсных трансформаторах.
Ферриты – это поликристаллические многокомпонентные соединения, изготавливаемыe по особой технологии, общая химическая формула которых MeFe2О3 (где Me – какой-либо ферромагнетик, например, Мn, Zn, Ni). Ферриты обладают высокими значениями собственного омического сопротивления, превышающего сопротивление сталей в 50 и более раз. Именно это обстоятельство позволяет применять ферриты в индуктивных элементах, работающих на высоких частотах, без опасения, что могут повыситься потери на вихревые токи. Наибольшее распространение в силовой технике получили марганец-цинковые ферриты марок НМ и никель-цинковые ферриты марок НН. При выборе между ними предпочтение, конечно, следует отдать ферритам марок НМ, поскольку они имеют более высокую температуру, при которой ферромагнетики теряют свои ферромагнитные свойства (температуру Кюри). Это обстоятельство позволяет эксплуатировать их при более высоких температурах перегрева. Потери на гистерезис у марганец-цинковых ферритов на порядок меньше, чем у никель-цинковых. Ферриты марок НМ обладают высокой стабильностью к воздействию механических нагрузок. Однако, омическое сопротивление ферритов марок НМ меньше, чем ферритов марок НН, поэтому последние могут применяться для работы на более высоких частотах.
Отметим из наиболее часто встречающихся никель-цинковые ферриты марок 2000НН, 1000НН, 600НН, 200НН, 100НН. Верхней границей рабочей области частот для них является 5-7 МГц. Марганцево-цинковые высокопроницаемые ферриты марок 6000НМ,4000НМ, З000НМ, 2000НМ, I500HM, 1000НМ используются в частотном диапазоне до нескольких сот килогерц в интервале температур -60...+100 °С, когда термостабильность не является определяющим параметром. В противном случае следует использовать термостабильные ферриты 2000НМ3, 2000НМ1, 1500НМ3, 1500НМ1, 1000HM3, 700НМ. Они обладают меньшими потерями на вихревые токи и большим диапазоном частот (0,3...1,5 МГц). Для импульсных источников термостабильность, конечно, важна, но не является определяющим фактором. На рисунке ниже показана зависимость В(Н) для феррита 1500НМ3 при различных температурах и частотах: 1 – 20 кГц; 2 – 50 кГц; 3 – 100 кГц.
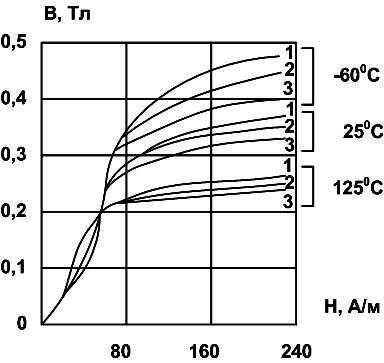
В средних и, особенно, сильных полях хорошо применять ферриты марок 4000НMC, 3000HMC, 2500НМС1, 2500НМС2. Результаты исследований показывают, что лучшими представителями в этой группе являются ферриты 2500НМС1 и 2500НМС2. Зависимость В(Н) для феррита 2500НМС1 при частоте 20 кГц показана ниже.
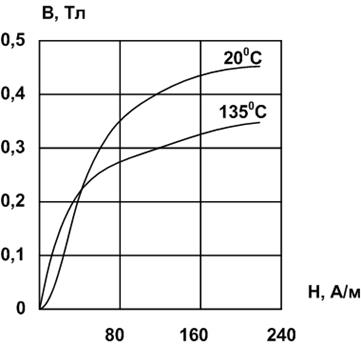
Параметры ферритов марок 2500НМС1 и 2500НМС2 сведены в таблицу.
| Параметр | Обозн | Ед. изм. | 2500НМС1 | 2500НМС2 |
| Начальная магнитная проницаемость при В = 0,2 тл, f = 16 кГц | μн | - | 4500 (при 200С) 4100 (при 1200С) | 4500 (при 200С) 4100 (при 1200С) |
| Критическая частота | F0 | МГц | 0,4 | 0,4 |
| Удельные объемные магнитные потери при В = 0,2 тл, f = 16 кГц | Psp | мкВт см3Гц | 10,5 (при 250С) 8,7 (при 1000С) | 8,5 (при 250С) 6,0 (при 1000С) |
| Магнитная индукция при H=240 А/м | В | мтл | ||
| Индукция насыщения | Вm | мтл | ||
| Остаточная магнитная индукция | Вr | мтл | ||
| Температура Кюри | Тс | 0С | >200 | >200 |
| Плотность | г/см3 | |||
| Удельное электрическое сопротивление | ρ | Ом*м | 4,9 | 4,9 |
Наши рекомендации
|
