Характеристики волнового процесса

Поскольку волна - это процесс распространения колебаний в пространстве, то для волнового процесса используются те же характеристики, что и для колебаний (T , ν ,φ ,ω ,A ), но вводятся еще и новые характеристики. Такими характеристиками являются: скорость волны - v, длина волны - λ, волновое число - k. При волновых процессах вводятся такие понятия, как фронт волны и волновая поверхность.

Фронтом волны называется поверхность, которая отделяет часть пространства, уже вовлеченную в волновой процесс, от области, в которой колебания еще не возникли.

Волновой поверхностью называется геометрическое место точек, колеблющихся в одинаковой фазе.

Волновых поверхностей существует бесчисленное множество, в то время как фронт волны один. Простейшие волновые поверхности - плоскости и сферы. Если волновые поверхности представляют собой плоскости, то волна называется плоской, если они представляют собой множество концентрических сфер, то это сферическая волна. На больших расстояниях от точечного источника можно небольшие участки волновой поверхности считать плоскими.

Скоростью волны v называется скорость перемещения волновой поверхности (фазовая скорость). Экспериментально ее можно найти, определив скорость перемещения фронта волны.

Длиной волны λ называется расстояние, пройденное волновой поверхностью за период колебаний. Длина волны вычисляется по формуле

Связь длины волны и частоты дается формулой

Волновым числом называется величина

Уравнение плоской гармонической волны

Уравнением волны называется выражение, которое определяет смещение колеблющейся частицы как функцию координат и времени.

Найдем вид уравнения для плоской гармонической волны.

Пусть в начале координат находится источник плоских волн, которые распространяются вдоль оси x. Смещение точек среды в плоскости x = 0 совершается по гармоническому закону:

.

Найдем вид функции, описывающий колебания точек в некоторой плоскости x. Для того, чтобы волна прошла путь от источника до точки наблюдения, требуется время 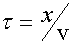, где v - фазовая скорость распространения волны (рис. 3.5).

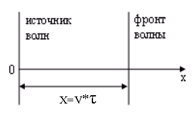
Рис.3.5

Поэтому уравнение колебаний частиц, лежащих в плоскости x, будет иметь вид

Приведем это уравнение к симметричному виду:

.

Найдем, чему равно отношение 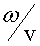, используя формулы (3.3), (3.20) и (3.22):

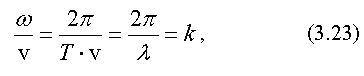
где k - волновое число.

Тогда получим уравнение плоской волны:

где A - амплитуда волны,
- фаза волны, т. е. фаза колебаний в точке с координатой x.

Формула (3.18) показывает, что смещение ξ зависит от времени t и координаты x - координаты положения равновесия колеблющейся частицы среды.

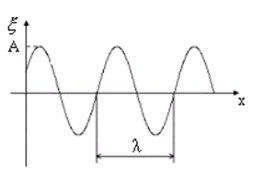
Рис.3.6

На рис. 3.6 представлен график зависимости смещения от координаты при t = const (формула (3.24)). На этом рисунке показаны амплитуда волны A и длина волны λ.

Энергия упругой волны

Распространение волн связано с переносом энергии. При этом частицы среды не переносятся волной, а совершают колебание около положения равновесия. Скорость колеблющейся частицы, в соответствии с формулами (3.11) и (3.24), равна

.

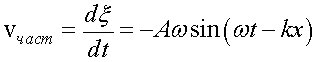Кинетическая энергия частиц, заключенных в объеме , равна (см. формулу (1.29))

.

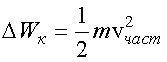Масса выделенного объема m равна

,

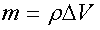где ρ - плотность среды.

Тогда значение кинетической энергии выделенного объема равно

.

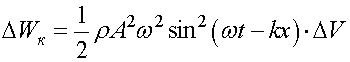Выделенный объем обладает также потенциальной энергией 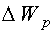. Можно показать, что

,

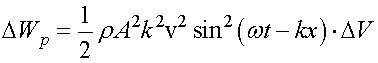где, согласно формуле (3.23), .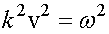

Следовательно, кинетическая энергия выделенного объема равна потенциальной энергии.

Полная энергия равна сумме кинетической и потенциальной энергии

.

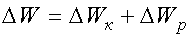Полная энергия, возникающая в упругой среде при распространении в ней плоской гармонической волны, равна

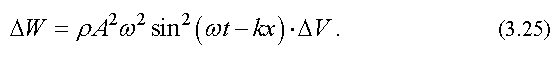
Плотностью энергии называется энергия, заключенная в единице объема, т. е.

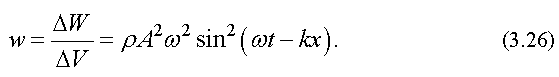
Из формулы (3.26) следует, что плотность энергии в каждый момент времени в разных точках пространства различна. Среднее значение плотности энергии определяется средним значением квадрата синуса

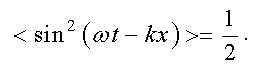
Следовательно, среднее по времени значение плотности энергии в данной точке среды равно

Итак, энергия волны (3.25), плотность энергии (3.26) и ее среднее значение (3.27) пропорциональны плотности среды, квадрату амплитуды и квадрату частоты.

Электромагнитные волны

Электромагнитными волнами называется процесс распространения в пространстве переменного электромагнитного поля. Теоретически существование электромагнитных волн предсказано английским ученым Максвеллом в 1865 г., а впервые они экспериментально получены немецким ученым Герцем в 1888 г.

Из теории Максвелла вытекают формулы, описывающие колебания векторов 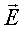и 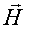. Плоская монохроматическая электромагнитная волна, распространяющаяся вдоль оси x, описывается уравнениями

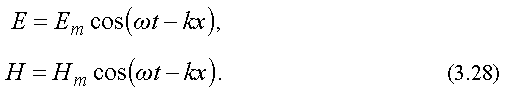
Здесь E и H - мгновенные значения, а E_m и H_m - амплитудные значения напряженности электрического и магнитного полей, ω - круговая частота, k - волновое число. Векторы 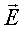и 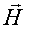колеблются с одинаковой частотой и фазой, взаимно перпендикулярны и, кроме того, перпендикулярны вектору 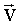- скорости распространения волны (рис. 3.7). Т. е. электромагнитные волны поперечны.

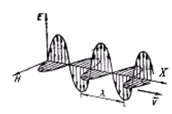
Рис.3.7

В вакууме электромагнитные волны распространяются со скоростью 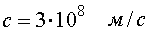. В среде с диэлектрической проницаемостью ε и магнитной проницаемостью µ скорость распространения электромагнитной волны равна:

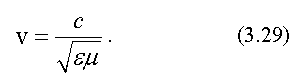
Частота электромагнитных колебаний, так же, как и длина волны, могут быть в принципе любыми. Классификация волн по частоте (или длине волны) называется шкалой электромагнитных волн. Электромагнитные волны делятся на несколько видов.

Радиоволны имеют длину волны от 10³ до 10^-4 м.

Световые волны включают:

· инфракрасное излучение,

· видимый свет в интервале ,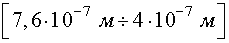

· ультрафиолетовое излучение.

Рентгеновское излучение - .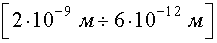

Гамма-излучение имеет длину волны < 10^-12 м.

Световые волны

Световые волны - это электромагнитные волны, которые включают в себя инфракрасную, видимую и ультрафиолетовую части спектра. Длины световых волн в вакууме, соответствующие основным цветам видимого спектра, указаны в нижеприведенной таблице. Длина волны дана в нанометрах, .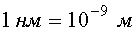

Таблица

Цвет	Длина волны, нм	Цвет	Длина волны, нм
красный	760 - 620	голубой	510 - 480
оранжевый	620 - 590	синий	480 - 450
желтый	590 - 575	фиолетовый	450 - 380
зеленый	575 - 510

Для световых волн характерны те же свойства, что и для электромагнитных волн.

1. Световые волны поперечны.

2. В световой волне колеблются вектора 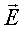и .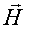

Опыт показывает, что все виды воздействий (физиологическое, фотохимическое, фотоэлектрическое и др.) вызываются колебаниями электрического вектора 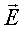. Его называют световым вектором. Уравнение световой волны имеет сведующий вид

Амплитуду светового вектора E_m часто обозначают буквой A и вместо уравнения (3.30) используют уравнение (3.24).

3. Скорость света в вакууме .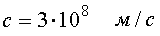

Скорость световой волны в среде определяется по формуле (3.29). Но для прозрачных сред (стекло, вода) обычно 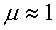, поэтому .

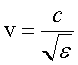Для световых волн вводится понятие - абсолютный показатель преломления.

Абсолютным показателем преломления называется отношение скорости света в вакууме к скорости света в данной среде

Из (3.29), с учетом того, что для прозрачных сред 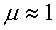, можно записать равенство .

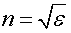Для вакуума ε = 1 и n = 1. Для любой физической среды n > 1. Например, для воды n = 1,33, для стекла 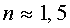. Среда с большим показателем преломления называется оптически более плотной. Отношение абсолютных показателей преломления называется относительным показателем преломления:

4. Частота световых волн очень велика. Например, для красного света с длиной волны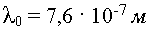

.

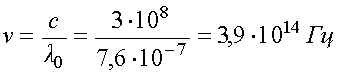При переходе света из одной среды в другую частота света не изменяется, но изменяется скорость и длина волны.

Для вакуума - 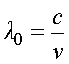; для среды - 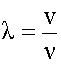, тогда

.

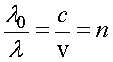Отсюда длина волны света в среде равна отношению длины волны света в вакууме к показателю преломления

5. Поскольку частота световых волн очень велика , то глаз наблюдателя не различает отдельных колебаний, а воспринимает усредненные потоки энергии. Таким образом вводится понятие интенсивности.

Интенсивностью называется отношение средней энергии, переносимой волной, к промежутку времени и к площади площадки, перпендикулярной направлению распространения волны:

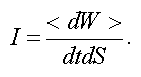
Поскольку энергия волны пропорциональна квадрату амплитуды (см. формулу (3.25)), то интенсивность пропорциональна среднему значению квадрата амплитуды

Характеристикой интенсивности света, учитывающей его способность вызывать зрительные ощущения, является световой поток - Ф.

6. Волновая природа света проявляется, например, в таких явлениях, как интерференция и дифракция.

Задания и вопросы для самоконтроля

1. Что называется волной? Приведите примеры волн.

2. Что называется фронтом волны? Волновой поверхностью?

3. Назовите характеристики волнового процесса и дайте их определения.

4. Как получить уравнение плоской волны?

5. От чего зависит энергия и плотность энергии волн?

6. Что такое электромагнитная волна? Какова скорость ее распространения?

7. Что представляет собой шкала электромагнитных волн?

8. Что называется световым вектором?

9. Дайте определение абсолютного и относительного показателей преломления.

10. Что называется интенсивностью?

Волновая оптика

Явление интерференции света

Волны, как и колебания, могут складываться. Сложение волн может быть интерференционным и неинтерференционным. Интерференцией называется сложение когерентных волн, при котором в разных точках пространства получается усиление или ослабление амплитуды результирующей волны, не изменяющееся с течением времени. Интерференция наблюдается только от когерентных источников. Когерентность - значит согласованность. Когерентными источниками называются такие источники, которые дают волны одинаковой частоты, и для фиксированной точки пространства разность фаз колебаний остается постоянной.

Независимые источники света не могут быть когерентными, так как в каждом из них свет испускается множеством атомов, излучающих несогласованно. Разность фаз колебаний, испускаемых совокупностью атомов таких источников, быстро и беспорядочно меняется во времени. Когерентность можно обеспечить, разделив волну от одного источника на две части и затем сведя их вместе. Две части одной волны когерентны между собой и при наложении будут интерферировать.

Существуют различные методы получения когерентных световых источников. Самый простой из них - метод Юнга, в котором световая волна делится на две части с помощью экрана с двумя узкими параллельными щелями.

3.3.2. Условия максимума и минимума интенсивности
при интерференции

Найдем условия максимума и минимума интенсивности при интерференции. Пусть S₁ и S₂ - два когерентных источника, совершающих колебания в одинаковой фазе. До точки наблюдения М волны проходят разное расстояние (рис. 3.8).

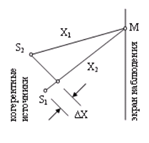
Рис.3.8

Запишем для них уравнения волн (3.24)

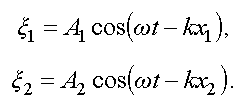
Найдем разность фаз складываемых волн

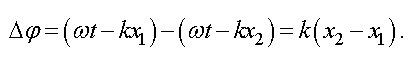
Обозначим через Δx - разность хода, т. е. 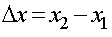. По формуле (3.22) волновое число равно , тогда связь между разностью хода и разностью фаз дается уравнением

Амплитуда результирующего колебания в точке наблюдения определяется уравнением (3.16)

.

Так как интенсивность пропорциональна среднему значению квадрата амплитуды (см. (3.34)): 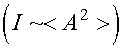, то получим выражение для результирующей интенсивности

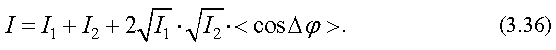
Если источники некогерентные, то и , т. е. интерференция не наблюдается. Для когерентных источников разность фаз 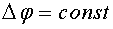и среднее значение косинуса равно косинусу разности фаз

.

В тех точках пространства, где интенсивность 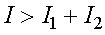, а там, где интенсивность . Следовательно, при наложении двух когерентных световых волн происходит пространственное перераспределение световой энергии, в результате чего в одних местах возникают максимумы, а в других - минимумы интенсивности, т. е. появляется интерференционная картина.

Максимумы интенсивности появляются там, где 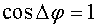, т. е. при , где m = 0, 1, 2, ... Следовательно, . Отсюда получим условие максимума интенсивности при интерференции

где m - порядок интерференционного максимума.

Условие максимума интенсивности при интерференции читается следующим образом.

Если разность хода равна целому числу длин волн или четному числу полуволн, то будет наблюдаться максимум интенсивности при интерференции.

Аналогично найдем условие минимума. Если 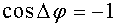, то 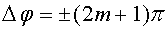, где m = 0, 1, 2, ...

Тогда

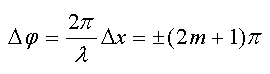
и

Условие минимума интенсивности при интерференции читается следующим образом.

Если разность хода равна нечетному числу полуволн, то в данной точке экрана будет наблюдаться минимум интенсивности при интерференции.