Интерференция в тонких пленках

Пленкой будет называться прозрачный слой, толщина которого сравнима с длиной волны. Плоская монохроматическая волна падает на прозрачную пленку толщиной d и показателем преломленияn под углом i. Луч 1 падающий на пленку в точке А, частично отразится (луч 1^'), а частично преломится под углом r и войдет в пленку. Дойдя до точки D, он частично преломится в воздух (n_возд @ 1), а частично отразится от нижней грани пленки и пойдет к точке С. Здесь он опять частично отразится и преломится. Часть луча 1 снова выйдет в воздух в этой точке под углом i. Но в точку С попадет и частично отраженный под тем же углом луч 2. На фронте АBоба луча имеют одинаковую фазу, но в дальнейшем проходят различные пути в различных средах. Оптическая разность хода, приобретаемая этими лучами, выразится:

. (3.4.13)

Из рис. 3.4.2. видно, что

. (3.4.14)

Учитывая, что 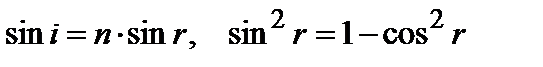, получим:

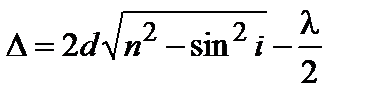(3.4.15)

Известно, что при отражении света от оптически более плотной среды фаза колебаний сменяется на p, а оптическая разность хода на 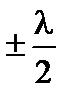. В данном случае следует взять 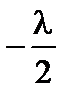, т.к. отражение от более плотной среды происходит в точке А, следовательно, « теряет » фазу луч 2. Таким образом, при падении на пленку плоской волны образуется две отраженные волны, разность хода которых определяется выражением

. (3.4.16)

Эти волны могут интерферировать при соблюдении условий временной когерентности.

Если освещать пленку монохроматическим светом, то при выполнении условия

– условие максимума,(3.4.17)

она будет иметь цвет источника монохроматического излучения.

При условии

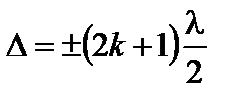– условие минимума,(3.4.18)

пленка будет темной.

При освещении пленки данной толщины белым светом под определенным углом максимум интерференции будет приходится на определенную длину волны, и пленка окажется окрашенной в цвет, соответствующий этой длине волны.

Полосы равного наклона

Согласно (3.4.16) при освещении плоскопараллельной пленки (d = const) монохроматическим светом (l = const) результаты интерференции в различных точках экрана зависят только от углов падения i.

Рис. 3.4.3.

Все лучи падающие на пленку под определенным углом i = const (например, луч S и все параллельные ему), соберутся на экране в одной точке С (рис. 3.4.3). Лучи другого наклона (например, лучи, параллельные S^') соберутся в другой точке С^'. В общем случае имеется семейство точек, для которых i = const, т.е. получится интерференционная полоса равного наклона. Так как положение максимумов зависит от длины волны l (условие 8), то в белом свете получится совокупность смещенных друг относительно друга полос, образованных лучами разной длины волны, и интерференционная картина приобретает радужную окраску.

Полосы равной толщины

Рис. 3.4.4.

Если пленка имеет переменную толщину, например, клин, и освещается параллельным пучком лучей, то разность хода определяется только толщиной пленки (рис. 3.4.4). Эта разность хода сохраняется постоянной только вдоль линий, параллельных ребру клина и убывает в направлении ребра клина. Поэтому поверхность пленки будет покрыта чередующимися светлыми и темными полосами, параллельными ребру, называющимися полосами равной толщины. Частным случаем полос равной толщины являются кольца Ньютона.

Кольца Ньютона

Если наложить сферическую линзу на плоское стекло, то получим воздушный слой (n = 1) переменной толщины (рис. 3.4.5).

В

А

Рис. 3.4.5.

Интерференционные полосы, возникающие в такой системе, имеют вид концентрических окружностей, которые называются кольцами Ньютона.

Рассчитаем радиусы колец Ньютона. При нормальном падении лучей и большом радиусе кривизны R поверхности линзы можно пренебречь различными углами падения лучей на сферическую поверхность. Оптическая разность хода для данного случая

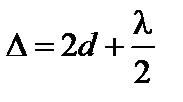. (3.4.19)

Из рис. 3.4.5 видно, что луч 1 отражается от оптически более плотной среды (точка А), а луч 2 – от оптически менее плотной среды (точка В), что ведет к возникновению дополнительной разности хода в полволны . Темные кольца (минимумы освещенности) образуются при условии

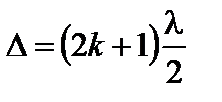, (3.4.20)

а светлые – при условии

. (3.4.21)

Толщина воздушного слоя d на расстоянии t (радиус кольца) от центра О при радиусе кривизны линзы R определяется из геометрических соображений:

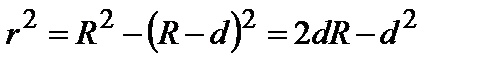. (3.4.22)

Пренебрегая членом как очень малым по сравнению с 2dr, находим

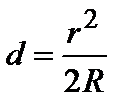. (3.4.23)

Подставляя это в (3.4.16) для темных колец, будем иметь

(3.4.24)

(в отраженном свете).

Отсюда радиусы этих колец равны

, (k = 0,1,2,3...), (3.4.25)

где k – порядковый номер темного кольца.

Для светлых колец имеем

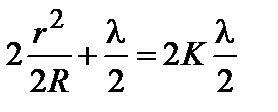. (3.4.26)

Отсюда радиусы светлых колец

, ( k = 0,1,2,3...). (3.4.27)

Измеряя радиусы колец Ньютона, и зная длину волны света, можно рассчитать радиус кривизны сферической поверхности линзы.

Если известен радиус кривизны линзы, то, измеряя радиусы колец в интерференционной картине, можно с большой точностью измерить длину волны падающего на линзу монохроматического света.

Таким образом, интерференционные полосы образуют концентрические окружности с темным пятном (минимумом) в середине – месте контакта. Это следует из выражения (3.4.16), т.к. при и, следовательно, колебания происходят в противофазе и гасят друг друга.

На практике трудно обеспечить контакт линзы с пластинкой в точке О, поэтому для расчетов обычно измеряют радиусы двух колец с номерами i и k.

. (3.4.28)

Отсюда

. (3.4.28)

Описание оборудования

Рис. 3.4.6.

В опытах используется микроскоп, на столике которого размещена линза Л, установленная на плоской пластинке с зачерненной нижней поверхностью (рис. 3.4.6). Свет от источника S через конденсатор K и светофильтр Ф направляется на полупрозрачную пластинку P. От пластинки лучи попадают на воздушный слой. Затем лучи, отраженные от верхней и нижней поверхности воздушного слоя, попадают в объектив микроскопа. Микроскоп фокусируется на верхнюю поверхность пластинки. По шкале микроскопа измеряют радиусы r' колец Ньютона.

Обработка результатов

Картина, наблюдаемая в микроскопе, есть увеличенное изображение действительных колец Ньютона. Радиусы действительных колец можно вычислить, зная увеличение микроскопа. В нашем случае увеличение равно 56, поэтому истинный радиус кольца равен

.

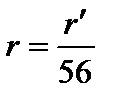Зная радиусы колец, по формуле (3.4.28) можно вычислить R. Данные вносим в таблицу:

№ п / п	№ колец	r', мм	r, мм	l, мм	R, мм
Ср.

Контрольные вопросы

1. Что такое интерференция и каковы условия её возникновения?

2. Чем отличаются оптическая и геометрическая разность хода лучей?

3. Каковы условия максимума и минимума интерференции?

4. Как происходит интерференция в тонких пленках?

4. Что такое кольца Ньютона и как они возникают?

5. Что такое полосы равной толщины и равного наклона?

6. Какая рабочая формула используется в работе (выведите её)?

Литература

1. Савельев И.В. Курс общей физики. Т.2.Учеб. пособие для студентов втузов. – М.: КНОРУС, 2009, 576 с.

2. Трофимова Т.И. Курс физики. Учеб. пособ. для вузов.- 15-е изд., стереотип. –М.: Издательский центр «Академия», 2007. –560 с.

3. Детлаф А.А., Яворский Б.М. Курс физики. Учеб пособие для втузов. – М: Высш. Шк., 1989. – 608 с.

ЛАБОРАТОРНАЯ РАБОТА № 3.5