Способы выражения состава фаз

Весовой и молярный состав

В технике состав выражают обычно в весовых долях (или весовых процентах), т. е. в виде отношения массы компонента в данной фазе к массе всей фазы. Если масса фазы , а масса содержащихся в ней компонентов А, В, С,... составляют соответственно , , , ..., то весовые доли компонентов будут:

; ; ... (1-1)

причем ... 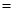1.

Во многих случаях состав выражают в молярных долях, т. е в виде отношения числа киломолей компонента в данной фазе к общему числу киломолей в этой фазе. Если всего в фазе кмоль, а число киломолей компонентов А, В, С, ... составляет , , ..., то молярные доли компонентов будут:

; ; ... (1-2)

причем .

Пересчет весового состава в молярный, или обратный пере-счет, производится следующим образом. Пусть весовой состав смеси , , , ..., а молекулярные массы компонентов , , , .... Тогда в 1 кг смеси содержатся следующие количества кмоль компонентов:

; ; ... (1-3)

а общее число кмоль составляет:

по формуле (16-2) находим молярный состав смеси:

; ; (1-4)

или в общем виде для -го компонента

Если задан молярный состав смеси , , , ..., то для пересчета его в весовой состав надо найти массы компонентов в 1 кмоль смеси:

; ;

и общую ее массу:

По формуле (16-1) находим весовой состав смеси:

; ; ...

или в общем виде для -го компонента:

Знаменатель этой формулы, представляющий собой массу 1 кмоль смеси, называется средней молекулярной массой смеси:

(1-5)

Состав смеси двух компонентов (двойные смеси) полностью характеризуется содержанием в ней лишь одного из компонен­тов. Пусть весовая и молярная доли этого компонента и . Тогда весовая и молярная доли другого компонента (1—а) и (1— ). Формулы (1-3) и (1-4) примут в этом случае сле­дующий вид:

(1-6)

(1-7)

где и — молекулярные массы компонентов.

Пример 1-1.Определить молярный состав и среднюю молекулярную массу смеси бензола и толуола, содержащей 30 вес. % бензола.

Р е ш е н и е. Молекулярные массы компонентов: (бензол) и (толуол). По формуле (1-6) находим молярную долю бензола в смеси (при а =0,3)

Молярная доля толуола (1—х) = 0,664. Эту же величину можно найти и по формуле (1-6), подставляя в нее весовую долю толуола а — 0,7, при этом М\ = 92 и М₂ = 78.

Средняя молекулярная масса смеси по формуле (1-5):

М_ср. = 78 • 0,336 + 92 • 0,664 = 87,2

Пример 1-2.Определить весовой состав смеси, содержащей 20 мол % этана, 35 мол % пропана, 15 мол. % бутана и 30 мол % изобутана.

Решение. Весовой состав определяем по формуле (1-4) и сводим результаты расчета в табл. 22.

Таблица 22

Результаты расчета весового состава смеси

Компоненты	Молекулярная Масса (Mk)	Молярная Доля (Xk)	мкхк	Весовая доля
Этан		0,20	6,0	0,126
Пропан		0,35	15,4	0,325
Бутан		0,15	8,7	0,183
Изобутан		0,30	17,4	0,366

Объемная концентрация

Состав выражают также через массу компонента, содержа­щегося в 1 м³ смеси (объемная концентрация). Объемная кон­центрация С имеет размерность кг/м³.

Сумма объемных концентрации всех компанентов ΣС равна массе 1 м³ смеси, т. е. плотности ρ. Таки образом, весовая доля k-го компанента смеси:

a_k=C_k/ρ (1-8)

Парциальное давление компанентов газовых смесей

Содержание компонентов газообразной смеси часто выражают через парциальное давление. Под парциальным давлением компанента понимают давление, под которым находился бы данный компанент, если в отсутствие других компанентов он занимал весь объем смеси при ее температуре.

Согласно закону Дальтона, полное давление Р газовой смеси равно сумме парциальных давлений компанентов p_А, р_В, р_с, …:

Р= p_А + р_{В, +} р_с +…

Как не трудно убедиться, отношение парциального давления компонента к полном давлению равно объемной доле компонента в смеси. В самом деле, если парциальное давление k-го компонента p_k, а объем газовой смеси V, то объем V_k, занимаемый этим компонентом при давлении P, определиться из соотношения p_kV=PV_k, откуда V_k=р_kV/Р, а объемная доля компонента в смеси

ϑ_k=V_k/V=p_k/P

Так как 1 кмоль любых компонента занимает при одинаковой температуре один и тот же объем, то объемная доля ϑk равна молярной доле у_k компонента в газовой смеси.

Таким образом

у_k= p_k/P или p_k=Р у_k (1-9)

Напишем уравнение состояния для 1 кг каждого компонента газовой смеси:

p_kV=RT/M_k

где p_k – парциальное давление k-го компонента, н/м²;

R - газовая постоянная (8314 Дж/кмоль · град);

M_k - молекулярная масса компонента.

Отсюда определяем объем V смеси, в котором находится 1 кг k-го компонента:

V=RT/ M_kp_k

Объемная концентрация компонента С_k=1/V, или

С_k= M_k p_k/RT (1-10)

Уравнение (1-9) устанавливает связь между парциальным давлением и молярной долей, уравнение (1-10) – между парциальным давлением и объемной концентрацией.

Пример 1-3. Смесь двуокиси углерода с воздухом содержит 15 объемн. % СО₂. Определить содержание СО₂ в смеси в вес. %, парциальное давление СО₂ в смеси и объемную концентрацию СО₂ при 25°С и общем (абсолютном) далении Р=19,6 бар (20 ат).

Решение. Для газовых смесей объемная доля компонента равна его молярной; следовательно, молярная доля двуокиси углерода у=0,15. Молекулярные массы составляют: М₁=44 (для СО₂) , М₂=29 (для воздуха).

Весовую долю СО₂ находим по формуле (1-7).

a=44 · 0,15/ 44 · 0,15 + 29 (1-0,15)=0,212, или 21,2 вес. %

Парциальное давление СО₂ определяем по уравнению (1-9)

Р = 19,6 · 0,15 = 2,94 бар (3 ат)

Объемная концентрация СО₂ по уравнению (1-10) составит,

С=44 · 2,94 · 10⁵/8314(273+25)=5,23 кг/м³

Относительный весовой состав

Состав двойной смеси можно выразить в виде отношения массы распределяемого компонента к массе носителя. Это отношение называется относительным весовым составом. Связь между относительным весовым составом Х и весовой долей а выражается следующим соотношением:

Х=а/1-а, или а=Х/1+Х (1-11)

При расчете состава газовой смеси, выраженный через парциальное давление компонента р, часто приходиться пересчитывать в относительно весовой состав. Это может быть сделано следующим образом. Если общее давление смеси Р, то парциальное давление носителя (Р - р); тогда уравнение состояние для компонента будет иметь вид

pV=Gk(R/M)T

и для носителя

(P - p)V=G_H(R/M_H)T

где V – объем смеси, м³;

G_K и G_H – количества компонента и носителя в объеме V, кг;

М_K и М_H – молекулярные массы компонента и носителя.

Деля первое уравнение на второе, получим:

p/P – p=G_K/G_H · M_H/M_K

Отсюда находим относительный весовой состав:

Y= G_K/G_H= M_K/M_H · p/P – p (1-12)

Пример 1-4. Найти относительный весовой состав смеси, рассмотренной в примере 1-3.

Решение. По формуле (1-11) находим

Y=0,212/ (1-0,212)=0,27 кг CO₂ на 1 кг воздуха

Если весовая доля не рассчитывалась, можно использовать формулу (1-12):

Y=44/29 · 2,94/(19,6-2,94)=0,27 кг СО₂ на 1 кг воздуха

Равновесие между фазами

Подобно тому как передача тепла протекает лишь при отклонении от состояния равновесия, т. е. при наличии разности температур между теплоносителями, так и переход вещества из одной фазы в другую происходит при отсутствии равновесия между фазами.

Пусть имеются две фазы и 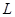, причем распределяемое вещество вначале находится только в первой фазе и имеет концентрацию . Если привести фазы в соприкосновение, то распределяемое вещество начнет переходить в фазу 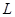. С момента появления распределяемого вещества в фазе 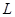начнется и обратный переход его в фазу .

Скорость обратного перехода будет увеличиваться по мере повышения концентрации распределяемого вещества в фазе 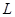. В некоторый момент скорости перехода вещества из фазы в фазу 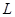и обратно станут одинаковыми. При этом установится состояние равновесия между фазами, при котором явного перехода вещества из одной фазы в другую происходить не будет.

В состоянии равновесия существует определенная зависимость между концентрациями распределяемого вещества в обеих фазах — любой концентрации 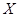этого вещества в фазе 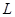соответствует равновесная концентрация его в фазе :

(1-13)

Условие равновесия, выраженное уравнением (1-13), позволяет определить направление процесса. Если рабочая концентрация распределяемого вещества в фазе больше равновесной ( > ), вещество будет переходить из фазы в фазу 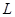. Если же < вещество переходит из фазы 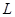в фазу .

Равновесие между фазами можно представить графически на — 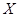-диаграмме (рис. 1-1). На этой диаграмме по оси абсцисс откладывается концентрация 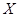распределяемого вещества в фазе 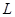, а по оси ординат — его концентрация в фазе . Кривая ОС, изображающая зависимость равновесной концентрации от 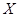, называется линией равновесия.

Конкретные уравнения условий равновесия будут рассмотрены при описании отдельных процессов.