Второй этап компактификации искривленных измерений
Подобно тому, как это было сделано в п. 13, выражение (20.5) можно свести к двум слагаемым
‹ds(–)2› + ‹ds(+)2› = ‹gij(+)›dxidxj + ‹gij(–)›dxidxj = 0, (21.1)
где
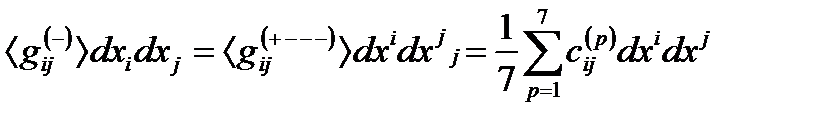 (21.2)
(21.2)
– квадратичная форма, являющаяся результатом усреднения семи метрик из (20.4) с сигнатурами, входящими в числитель левого ранжира (13.1) или (21.4);
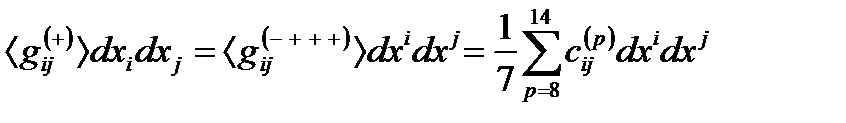 (21.3)
(21.3)
– квадратичная форма, являющаяся результатом усреднения семи усредненных метрик из (20.4) с сигнатурами, входящими в числитель правого ранжира (13.1) или (21.4).
| (+ + + +) (– – – + ) (+ – – + ) (– – + – ) (+ + – – ) (– + – – ) (+ – + – ) (+ – – – )+ | + + + + + + + + | (– – – – ) (+ + + – ) (– + + – ) (+ + – +) (– – + +) (+ – + +) (– + – +) (– + + +)+ | (21.4) |
Таким образом, из всей совокупности lm¸n-вакуумных флуктуаций можно выделить:
– усредненную «внешнюю» сторону 23-lm¸n-вакуумной протяженности (или усредненный субконт) с усредненной метрикой
ds(+ – – –)2 = ds(–)2 = gij(–)dxidxj с сигнатурой (+ – – –) (21.5)
где 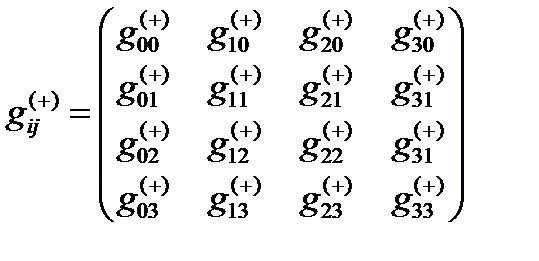 (21.6)
(21.6)
– усредненную «внутреннюю» сторону 23-lm¸n-вакуумной протяженности (или усредненный антисубконт) с метрикой
ds(– + + +)2 = ds(+)2 = gij(+)dxidxj с сигнатурой (– + + +), (21.7)
где 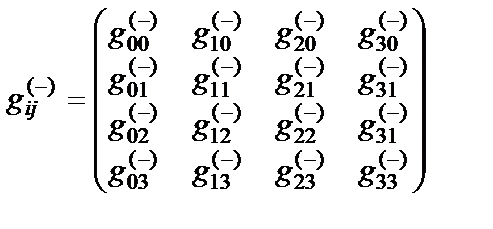 . (21.8)
. (21.8)
Для сокращения записей знаки усреднения в метриках (21.5) – (20.8) опущены.
На рис. 21.1 условно показан усредненный участок двухсторонней 23-lm¸n-вакуумной протяженности, внешняя сторона которой (субконт) описывается метрикой ds(–)2 (21.5) , а внутренняя сторона (антисубконт) – метрикой ds(+)2 (21.7).
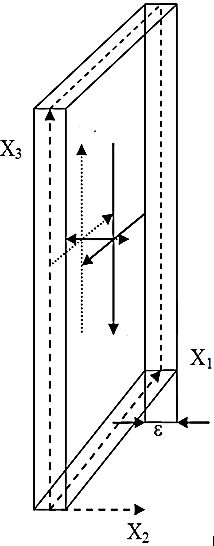
| Внутренняя 4-мерная сторона ВП ds(+)2 = gij(+)dxidxj , сигнатура(– + + +) |
| Внешняя 4-мерная сторона ВП ds(–)2 = gij(–)dxidxj , сигнатура (+ – – –) |
Рис. 21.1. Упрощенная иллюстрация участка двухсторонней 23-lm¸n-вакуумной протяженности (ВП),
внешняя сторона которой описывается 4-метрикой ds(–)2, а внутренняя сторона
– 4-метрикой ds(+)2, при ε → 0
21. Тензор 4-деформаций 23-lm¸n-вакуумной протяженности
Пусть исходное неискривленное метрико-динамическое состояние исследуемого участка внешней стороны 23-lm¸n-вакуумной протяженности (т.е. усредненного субконта) характеризуется усредненной метрикой
ds0(–)2 = gij0(–)dxi dxj с сигнатурой (+ – – –), (22.1)
а искривленное состояние того же участка задается усредненной метрикой
ds(–)2 = gij(–)dxi dxj с той же сигнатурой (+ – – –). (22.2)
Отличие искривленного состояния участка субконта от его неискривленного состояния определяется разницей вида (19.3)
ds(–)2 – ds0(–)2 = (gij(–) – gij0(–)) dxidxj = 2eij(–)dxidxj , (22.3)
где
eij(–) = ½ (gij(–) – gij0(–)) (22.4)
– тензор 4-деформаций локального участка субконта.
Относительное удлинение искривленного участка субконта равно [17]
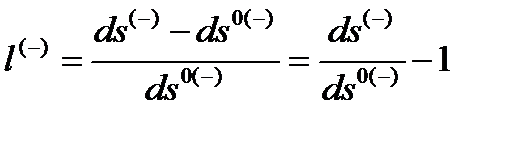 . (22.5)
. (22.5)
Откуда следует
ds(–)2 = (1 + l(–))2ds0(–)2. (22.6)
Подставляя (22.6) в (22.3) с учетом (22.4) имеем [17]
eij(–) = ½ [(1 + l(–))2 – 1] gij0(–), (22.7)
или в развернутом виде
eij(–) = ½ [(1 + li(–))(1 + lj(–)) cosbij(–) – cosbij0(–)] gij0(–), (22.8)
где
bij0(–) – угол между осями xi и xj системы отсчета, «вмороженной» в исходное неискривленное состояние исследуемого участка субконта;
bij(–) – угол между осями xi¢ и xj¢ искаженной системы отсчета «вмороженной» в искривленное состояние того же участка субконта.
При bij0(–) = p/2 выражение (22.8) принимает вид
eij(–) = ½ [(1 + li(–))(1 + lj(–)) cosbij(–) – 1] gij0(–). (22.9)
Для диагональных компонентов тензора 4-деформаций eii(–) выражение (22.9) упрощается
eii (–) = ½ [(1 + li(–))2 – 1] gii0(–), (22.10)
откуда следует [17]
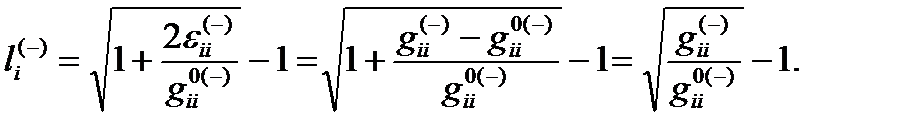 (22.11)
(22.11)
Если деформации eij(–) малы, то, разложив выражение (22.11) в ряд, и ограничившись первым членом ряда, получим относительное удлинение субконта
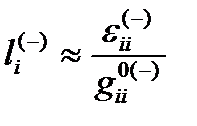 . (22.12)
. (22.12)
Аналогично, деформация локального участка внутренней стороны 23-lm¸n-вакуумной протяженности (усредненного антисубконта) определяется выражением
ds(+)2 – ds0(+)2 = (gij(+) – gij0(+))dxidx j = 2eij(+)dxidx j, (22.13)
где
eij(+) = ½ (gij(+) – gij0(+)) (22.14)
– тензор 4-деформаций локального участка антисубконта;
ds0(+)2 = gij0(+)dxi dxj с сигнатурой (– + + +) (22.15)
– метрика неискривленного состояние антисубконта;
ds (+)2 = gij(+)dxi dxj с той же сигнатурой (– + + +) (22.16)
– метрика искривленного состояние антисубконта.
Относительное удлинение антисубконта
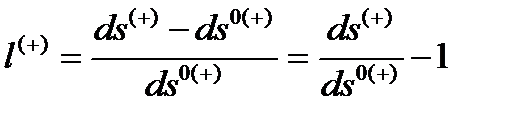 (22.17)
(22.17)
Определим тензор 4-деформаций двусторонней 23-lm¸n-вакуумной протяженности как среднее
eij(±) = ½ (eij(+) + eij(–)) = ½ (eij(– + + +) + eij(+ – – –)), (22.18)
или, с учетом (22.4) и (22.14)
eij(±) = ½ (gij(+) + gij(–)) – ½ (gij0(+) + gij0(–)) = ½ (gij(+) + gij(–)), (22.19)
т.к. согласно «вакуумному условию» (4.6):
gij0(+) + gij0(–) = gij0(– + + +) + gij0(+ – – –) = 0.
Относительное удлинение локального участка двухсторонней 23-lm¸n-вакуумной протяженности li(±) в этом случае следует вычислять с помощью формулы
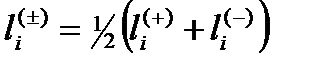 , (22.20)
, (22.20)
где
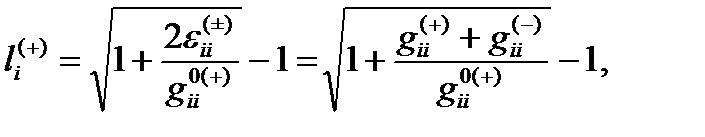
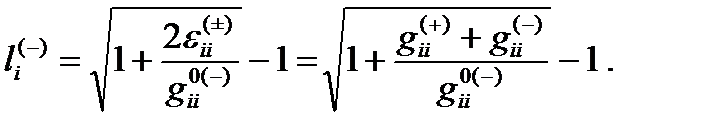 (22.21)
(22.21)
Поскольку в любом случае одна из компонент gij0(–) или gij0(+) является отрицательным числом, относительное удлинение (22.21) является комплексным числом.
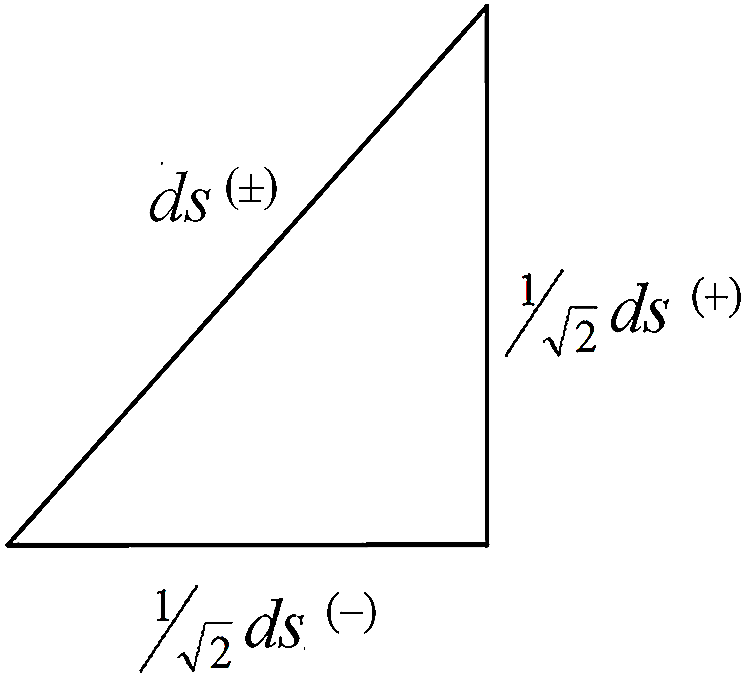 Рис. 22.1. Соотношение отрезков ds(–) и ds(+) Рис. 22.1. Соотношение отрезков ds(–) и ds(+) 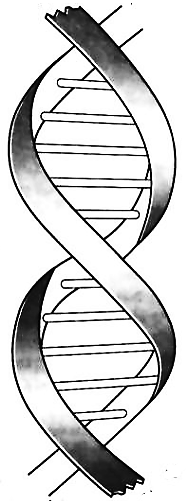 Рис. 22.2. Если спроецировать такую двойную спираль на плоскость, то в месте пересечения ее линии всегда взаимно перпендикулярны Рис. 22.2. Если спроецировать такую двойную спираль на плоскость, то в месте пересечения ее линии всегда взаимно перпендикулярны |
ds(±)2 = 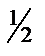 (ds(–)2+ ds(+)2) , (22.22)
(ds(–)2+ ds(+)2) , (22.22)
которая напоминает теорему Пифагора a2 + b2 = c2. Это означает, что отрезки линий ( 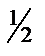 )1/2ds(–) и (
)1/2ds(–) и ( 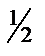 )1/2ds(+) всегда взаимно перпендикулярны по отношению друг к другу ds (–)^ ds (+) (рис. 22.1), а две линии, направленные в одном и том же направлении, могут быть всегда взаимно перпендикулярны только в том случае, когда они образуют двойную спираль (рис. 22.2).
)1/2ds(+) всегда взаимно перпендикулярны по отношению друг к другу ds (–)^ ds (+) (рис. 22.1), а две линии, направленные в одном и том же направлении, могут быть всегда взаимно перпендикулярны только в том случае, когда они образуют двойную спираль (рис. 22.2).
Таким образом, усредненная метрика (22.22) соответствует отрезку «жгута», состоящего из двух взаимно перпендикулярных спиралей s(–) и s(+). При этом, также как усредненное относительное удлинение (22.21), участок данной «двойной спирали» можно описать комплексным числом
ds (±)= 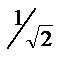 (ds (–)+ids (+)), (22.23)
(ds (–)+ids (+)), (22.23)
квадрат модуля которого равен (22.22).
Определение № 22.1k-жгут – это результат усреднения метрик с разными сигнатурами (где k – число усредняемых метрик, т.е. число «нитей» в «жгуте»).
В частности, усредненная метрика (22.22) называется 2-жгутом, так как она «скручена» из 2-х линий(«нитей»): ds(–) = ds (+ – – –) и ds(–) = ds(– + + +).
На следующем, более глубинном 16-стороннем, уровне рассмотрения метрико - динамические свойства локального участка 26-lm¸n-вакуумной протяженности характеризуются суперпозицией (т.е. аддитивным наложением или усреднением) шестнадцати 4-метрик со всеми 16-ю возможными сигнатурами (11.5), т.е. 16-жгутом:
dsS2 = 1/16 (ds(+ – – –)2 + ds(+ + + +)2 + ds(– – – +)2 + ds(+ – – +)2 +
+ ds(– – + –)2 + ds(+ + – –)2 + ds(– + – –)2 + ds(+ – + –)2 + (22.24)
+ ds(– + + +)2 + ds(– – – – )2 + ds(+ + + –)2 + ds(– + + –)2 +
+ ds(+ + – +)2 + ds(– – + +)2 + ds(+ – + +)2 + ds(– + – +)2) = 0.
В этом случае имеем 16 тензоров 4-деформаций всех типов 4-пространств
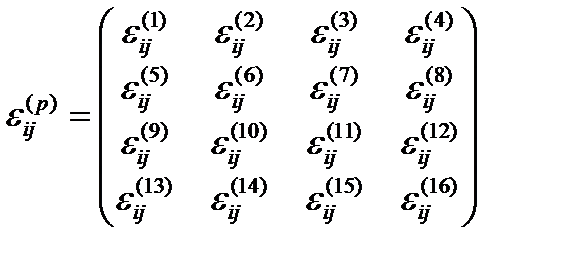 , (22.25)
, (22.25)
где eij(p) = ½ (сij(p) – сij0(p)) (22.26)
– тензор 4-деформаций p-го 4-подпространства.
сij0(p) – метрический тензор неискривленного участка p-го 4-подпространства;
сij(p) – метрический тензор того же, но искривленного участка p-го 4-подпространства.
При 16-стороннем уровне рассмотрения общий тензор 4-деформаций eii(16) локального участка 26-lm¸n-вакуумной протяженности равен
eij(16) = 1/16 (eij (1)+ eij (2)+eij(3)+eij(4)+eij(5)+eij(6)+eij(7)+eij(8)+eij(9)+
+eij(10)+eij(11)+eij(12)+eij(13)+eij(14)+eij(15)+eij(16)), (22.27)
а относительное удлинение локального участка вакуума 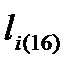 в этом случае следует вычислять по формуле
в этом случае следует вычислять по формуле
li (16) = η1 li (1)(16) + η2 li (2)(16) + η3 li (3)(16) +…+ η4 li (16)(16) , (22.28)
где
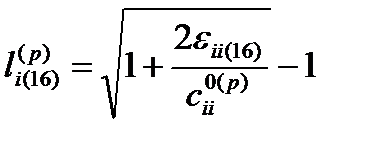 . (22.29)
. (22.29)
где ηm (где m = 1, 2, 3, … , 16) – ортонормированный базис объектов, удовлетворяющих антикоммутационному соотношению алгебры Клиффорда
ηmηn + ηnηm = 2δmn, (22.30)
где δnm – единичная 16´16-матрица.
При этом участок 16-жгута состоит из шестнадцати «нитей»:
ds (16) = η1 ds(+– – –) + η2 ds(+ + + +) + η3 ds(– – – +) + η4 ds(+ – – +) +
+ η5 ds(– – + –) + η6 ds(+ + – –) + η7 ds(– + – –) + η8 ds(+ – + –) + (22.31)
+ η9 ds(– + + +) + η10 ds(– – – –) + η11 ds(+ + + –) + η12 ds (– + + –) +
+ η13 ds(+ + – +) + η14 ds(– – + +) + η15 ds(+ – + +) + η16 ds(– + – +) = 0.
Если все линейные формы ds(+– – –), ds(+ + + +), … , ds(– + – +) удается представить в диагональном виде, то в соответствии с (14.13) в выражение (22.31) можно представить в спинтензорном виде
ds (16) = 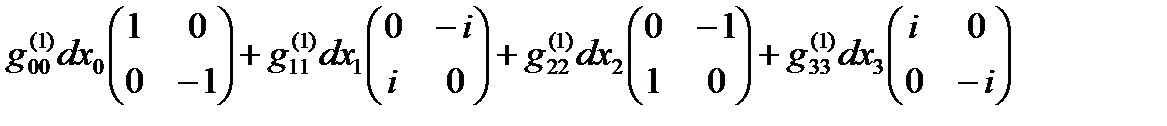 +
+
+ 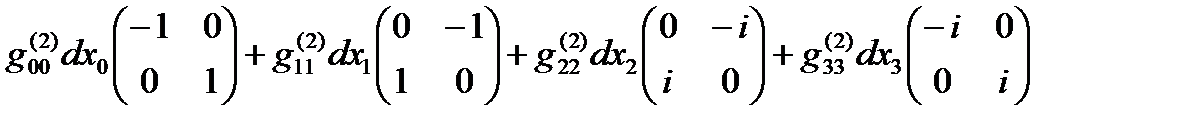 +
+
+ 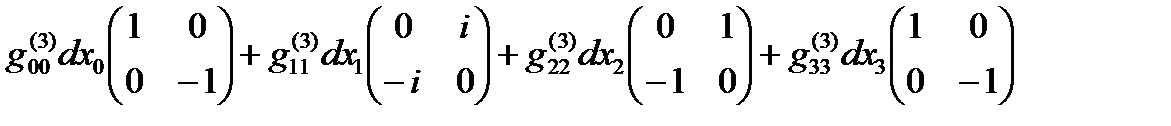 +
+
+ 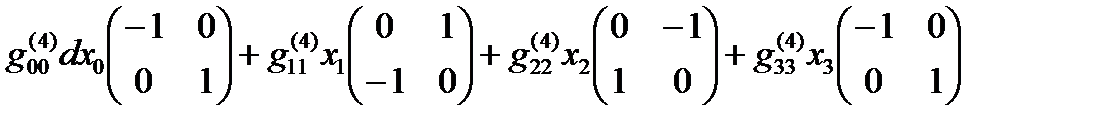 +
+
+ 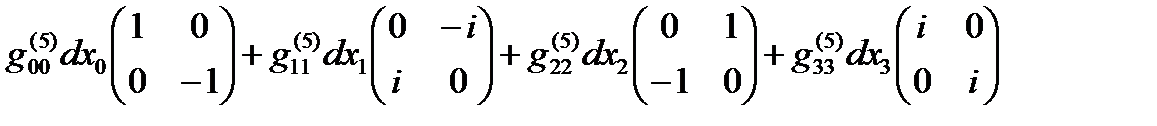 +
+
+ 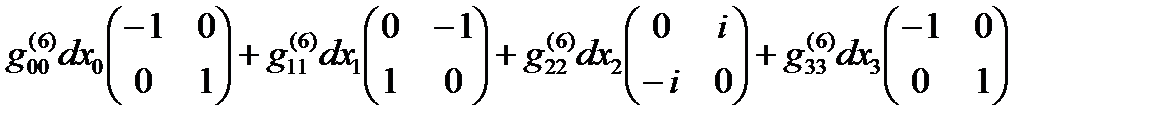 +
+
+ 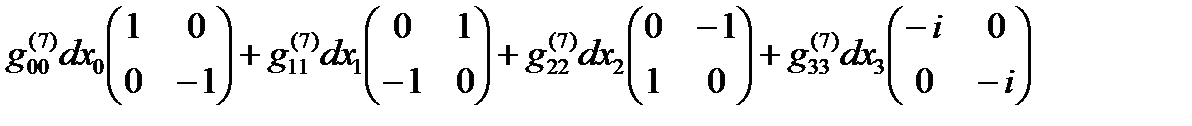 +
+
+ 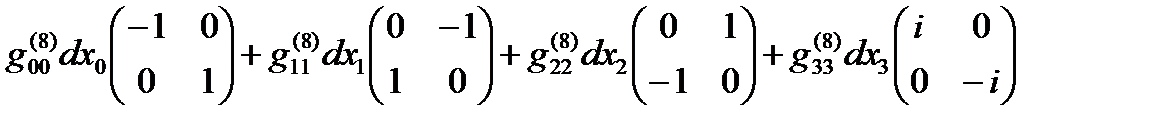 +
+
+ 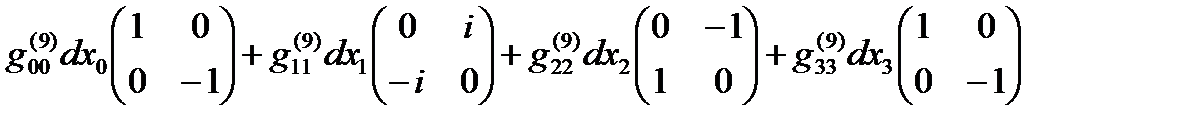 +
+
+ 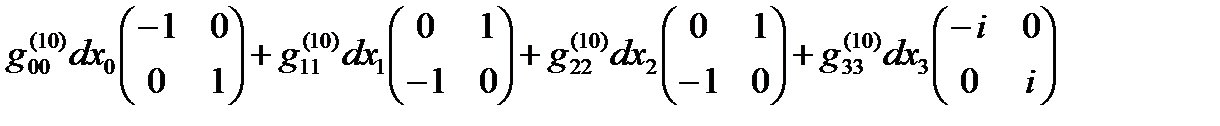 +
+
+ 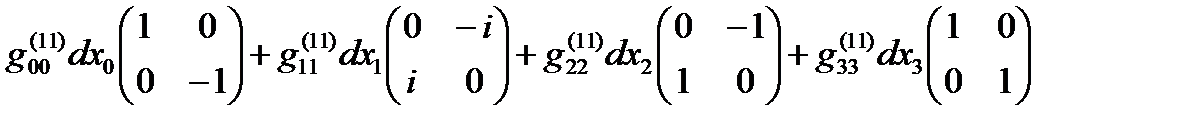 +
+
+ 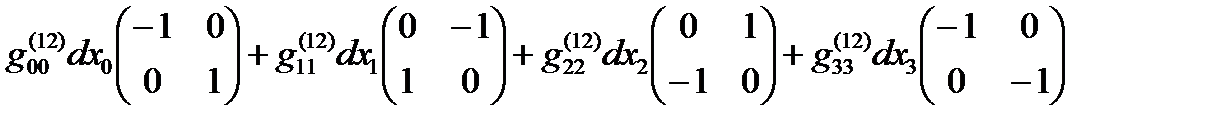
+ 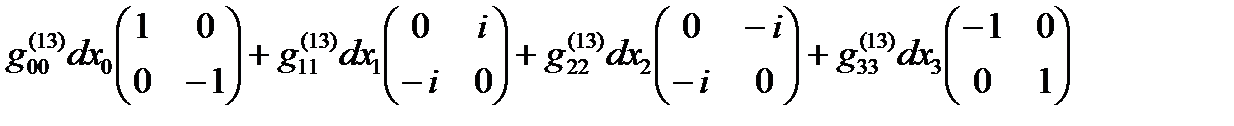 +
+
+ 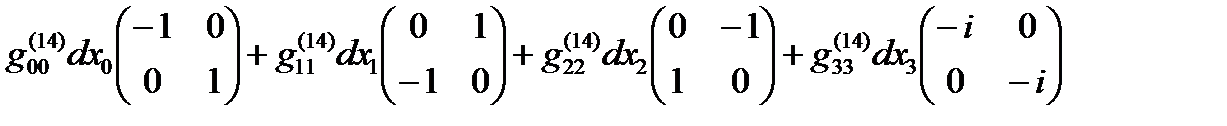 +
+
+ 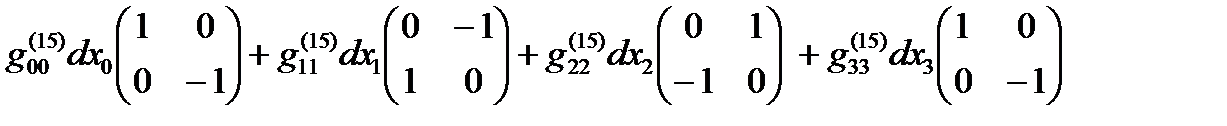 +
+
+ 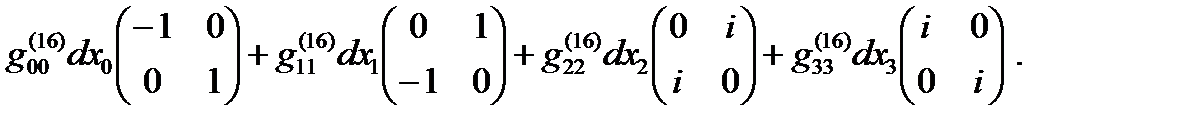 (22.32)
(22.32)
Возможны еще более глубинные 2n-сторонние уровни рассмотрения метрико - динамических свойств «вакуума» (пп. 1.2.9, 1.2.13 в [5]), с расширением количества компонент метрического тензора до бесконечности.
