Искривленные метрические 4-пространства

Для примера, рассмотрим два вектора (10.1) и (10.2), но заданных в 5-м и 7-м искривленных аффинных пространствах

ds¢ ⁽⁵⁾= β^ln(5)e_n⁽⁵⁾α_lj⁽⁵⁾dx^j, (18.1)

ds¢ ⁽⁷⁾= β^pm(7)e_m⁽⁷⁾α_pi⁽⁷⁾dxⁱ .(18.2)

Найдем скалярное произведение этих векторов

ds¢ ^(7,5)2 = ds¢ ⁽⁷⁾ds¢ ⁽⁵⁾ = β^pm(7)e_m⁽⁷⁾α_pi⁽⁷⁾β^ln(5)e_n⁽⁵⁾α_lj⁽⁵⁾dxⁱdx^j = с_ij^(7,5)dxⁱdx^j (18.3)

где

с_ij^(7,5)= β^pm(7)e_m⁽⁷⁾α_pi⁽⁷⁾β^ln(5)e_n⁽⁵⁾α_lj⁽⁵⁾ (18.4)

– компоненты метрического тензора (7,5)-го метрического 4-пространства.

Таким образом, получена метрика (7,5)-го метрического 4-пространства

ds¢ ^(7,5)2 = с_ij^(7,5)dxⁱdx^j (18.5)

с сигнатурой (10.5) (+ + + –) и метрическим тензором

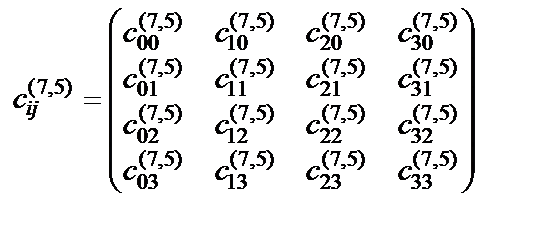. (18.6)

Аналогично скалярное попарное произведение двух любых векторов (17.9)

ds¢ ^(a)= β^pm(a)e_m^(а)α_pi^(a)dxⁱ (18.7)

ds¢ ^(b) = β^ln(b)e_n^(b)α_lj^(b)dx^j (18.8)

приводит к формированию атласа, состоящего из 16 × 16 = 256 всевозможных искривленных 4-листов (т.е. метрических 4-подпространств) с метриками

ds¢ ^{(a, b)2} = с_ij^{(a, b)}dxⁱdx^j, (18.9)

где а = 1, 2, 3, …,16; b= 1, 2, 3, …,16, с соответствующими сигнатурами (10.15) и метрическими тензорами

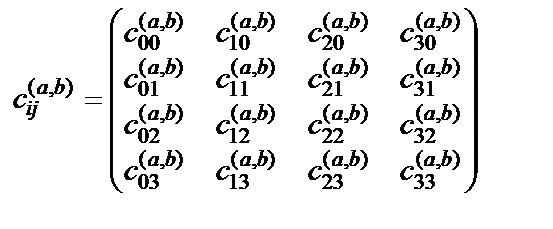, (18.10)

где

с_ij^{(a, b)}= β^pm(a)e_m^(a)α_pi^(a)β^ln(b)e_n^(b)α_lj^(b) (18.11)

– компоненты метрического тензора (a,b)-го искривленного метрического 4-подпространства.

Каждый из 256 метрических тензоров (18.10) это один из вариантов раскрытия Древа Сфирот, со своим (индивидуальным) набором метрико-динамических качеств

.

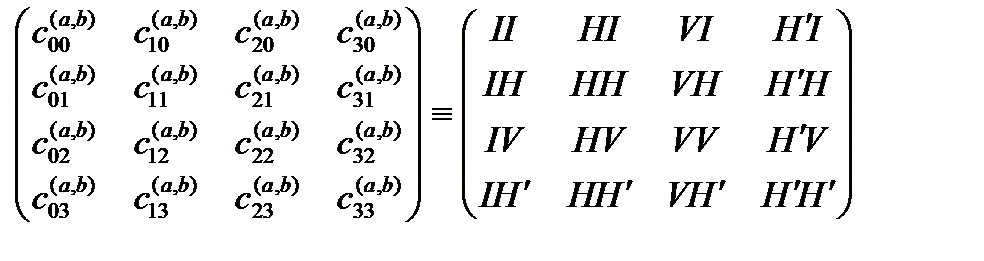где

(коц) II – Кетер (1 Сфира)

יHH – Хохма (2 Сфира)

הVV – Бина (3 Сфира)

ו IV, IH, IH¢, VH, VH¢, HH¢ – Заир Ампин (6 сдвоенных Сфирот)

VI, HI, H¢I, HV, H¢V, H¢H

ה H¢H¢ – Малхут (10 Сфира)

Тензор 4-деформаций

В классической теории упругости актуальное состояние локального объема упруго-пластичной среды, как правило, описывается только одной «вмороженной» в нее системой отсчета с соответствующим 4-базисом. Это приводит к анализу только одной квадратичной формы вида

ds¢ ² = g_ij dx^jdx^j , (19.1)

где g_ij – компоненты метрического тензора локального участка искривленной метрической протяженности (данных компонент 16, но из них действенными являются только 10, в силу симметрии g_ji = g_ij).

Квадратичную форму (19.1) сравнивают с квадратичной формой исходного, идеального состояния того же локального участка упруго-пластичной среды [17]

ds₀² = g_ij⁰ dxⁱ dx^j. (19.2)

Вычитая метрику исходного состояния (19.2) из метрики актуального состояния (19.1)

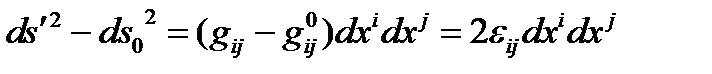, (19.3)

в теории сплошных сред определяется тензор 4-деформаций [17]

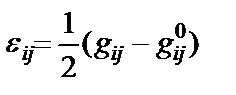, (19.4)

который является центральным предметом рассмотрения классической теории упругости.

Развиваемые здесь представления Алсигны отличаются от классических лишь тем, что исследуемый участок (куб) упруго-пластичной среды (в данном случае l_m¸n-вакуума) описывается не одним 4-базисом, связанным с одним из восьми углов исследуемого куба (рис. 17.1), а со всеми шестнадцатью 4-базисами (рис. 6.3), по два в каждой его вершине исследуемого куба.

Данное обстоятельство приводит к тому, что вместо одной метрики типа (19.1) в Алгебре сигнатур фигурирует 256 метрик (18.9)

ds^(a,b)2 = с_ij^(a,b)dxⁱ dx^j (19.5)

с соответствующими сигнатурами (10.15), которые описывают один и тот же объем, исследуемой протяженности (в частности «вакуума») с разных его сторон. При этом метрико-динамическое состояние исследуемого объема описывается не 16-ю числами (компонентами метрического тензора g_ji), а 256 ´ 16 = 4096-ю компонентами 256-ти тензоров с_ji^(a,b) (18.11). Этим достигается не только значительно более точное описание искривленного объема упруго-пластичной среды (в частности, l_m¸n-вакуума) в окрестности точки О (рис. 6.1), но обеспечивается логическое обоснование для выявления ряда более тонких вакуумных эффектов (которые планируется рассмотреть в следующих статьях).

Развиваемый Алсигной математический аппарат светогеометрии «вакуума» подходит для исследования не только «пустоты», но и любых других 3-мерных сплошных сред, в которых волновые возмущения (свет, звук, фононы) распространяются с постоянной скоростью.