Некоторые способы соединения 22-х букв Иврита
вא”רל(231) парные комбинации
Взято из комментариев
мудрецов ТОРЫ к Сефер га-Ецира (Книге Творения)
Таблицы 16.1
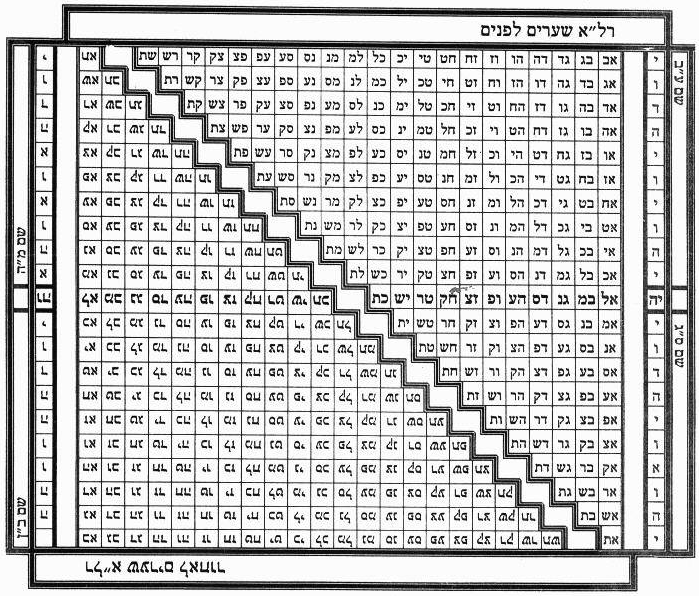
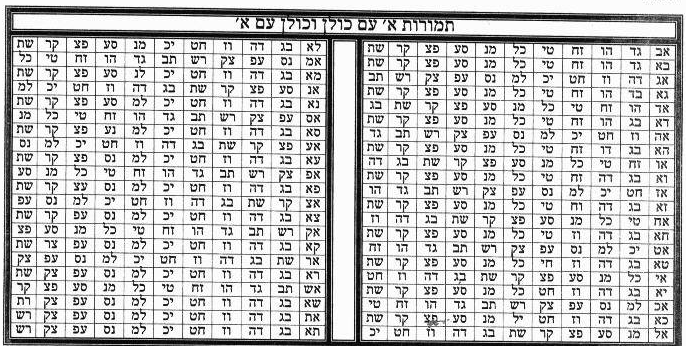
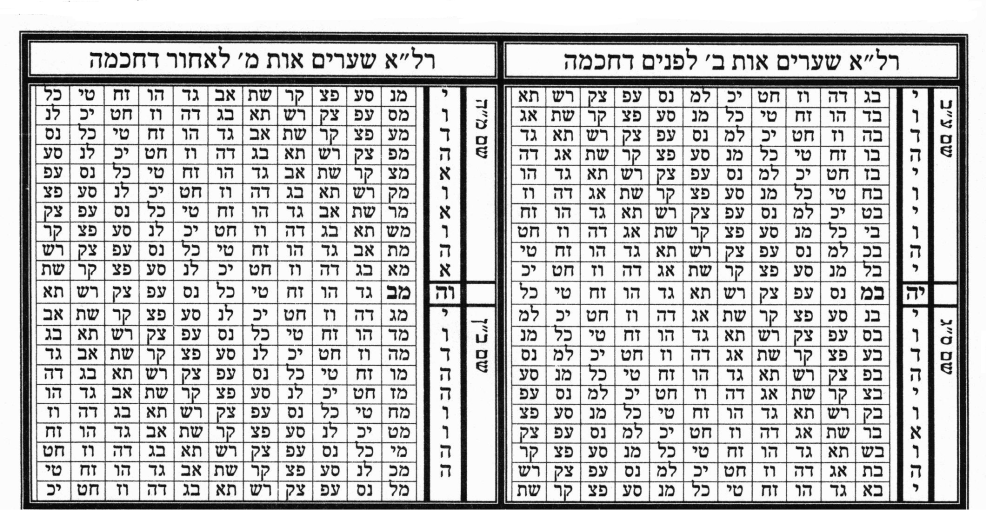
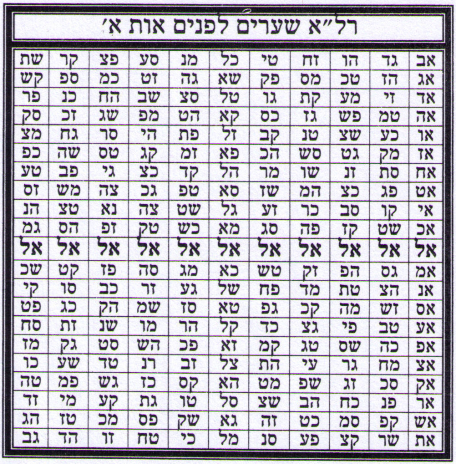
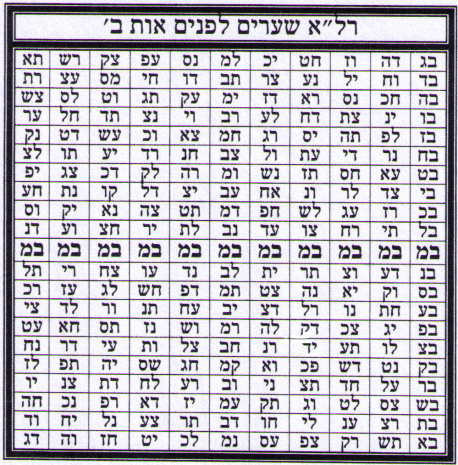
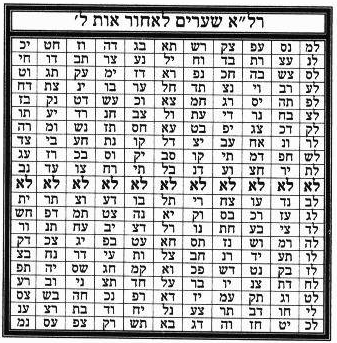
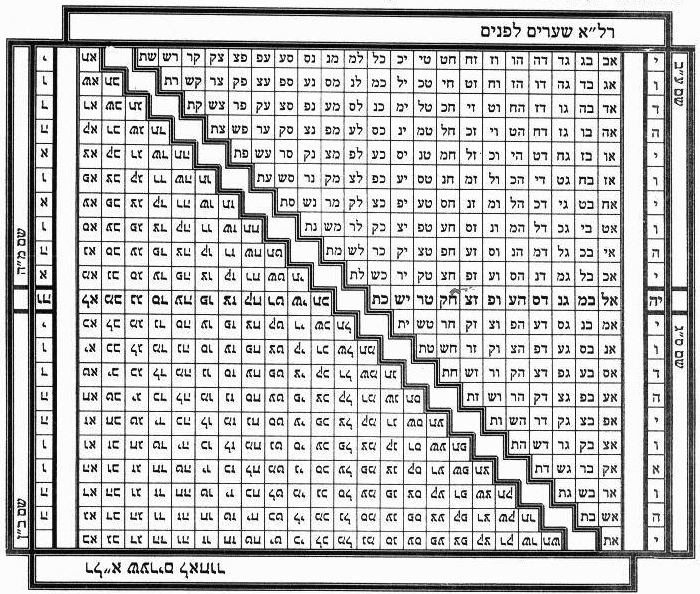
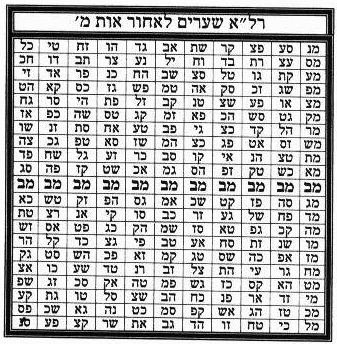
16а.2. Малбуш (Одеяние) из Света[4, 8]
Двадцать две Буквы Алфавита Хибру (Иврита) – это один из Алгоритмов раскрытия Великого и Грозного Имени ВСЕВЫШНЕГО
| יהוה |
| H’ V H I |
Всевозможные перестановки четырех Букв ТЕТРАГРАММАТОНА
ה-ו-ה-י≡ H'VHI (16.5)
приводят к составлению 4! = 24 Тетраграмматонных форм
I H' V H H I V H' V I H' H H' V I H
I H H' V H I H' V V H I H' H' V H I
I V H H' H H' I V V H' H I H' H V I (16.6)
I H V H' H H' V I V I H H' H' H I V
I V H' H H V I H' V H' I H H' I V H
I H' H V H V H' I V H H' I H' I H V
В Имени ה-ו-ה-י = H' V H I две буквы ה (Хей), поэтому среди 24 комбинаций (16.6) только 12 из них неповторяются. В каббале Они описывают цикличность времени: 12 комбинаций соответствуют 12 часам дня, другие 12 комбинаций – 12 часам ночи. Также данные Имена последовательно Влияют на 12 месяцев лунного года, т.д.
Если из 24-х Тетраграмматонных форм (16.6) вывести из рассмотрения само Непроизносимое Имя ה-ו-ה-י = H' V H I (которое присутствует в Тексте ТОРЫ как самостоятельная Единица) и противоположное (сопряженное) ему Антиимяה-ו-ה-י= I H V H', то останутся 22 Тетраграмматонные формы, с которыми можно сопоставить 22 буквы еврейского Алфавита:
V H I H' I H H' V H I H' V I H' V H H I V H' V I H' H H' V I H
א ב ג ד ה ו ז
H' H I V I V H' H I V H H' H H' I V V H' H I H' H V I V H H' I
ט י כ ל מ נ ח
H V I H' V H' I H H' I V H H V H' I H H' V I V I H H' I H' H V
ס ע פ צ ק ר ש
H' I H V (16.7)
ת
Прямой и обратный лучи света, лежащие в основе светогеометрии «вакуума», также описываются выражениями, содержащими по четыре слагаемых
H' V H I i
dz + dy + dx – cdt = 0, (16.8)
i I H V H'
0 = cdt – dz – dy – dx. (16.9)
Из 4-х слагаемых линейных форм (16.8) и (16.9) составляются 22 парные (сопряженные) комбинации, аналогичные 22-м Тетраграмматонным формам (16.7):
dy+dx–cdt+dz –cdt+dx+dz+dy dx–cdt+dz+dy –cdt+dz+dy+dx dx–cdt+dy+dz dy–cdt+dz+dx dz+dy–cdt+dx
–dy–dx+cdt–dz cdt–dx–dz–dy –dx+cdt–dz–dy cdt–dz–dy–dx –dx+cdt–dy–dz –dy+cdt–dz–dx –dz–dy+cdt–dx
V H I H' I H H' V H I H' V I H' V H H I V H' V I H' H H' V I H
א ב ג ד ה ו ז
dz+dx–cdt+dy –cdt+dy+dz+dx –cdt +dy+dx+dz dx+dz–cdt+dy dy+dz+dx–cdt dz+dx+dy–cdt dy+dx +dz–cdt
– dz–dx+cdt–dy cdt–dy–dz–dx cdt–dy–dx–dz –dx–dz+cdt–dy –dy–dz–dx+cdt –dz–dx–dy+cdt –dy–dx–dz+cdt
H' H I V I V H' H I V H H' H H' I V V H' H I H' H V I V H H' I
ט י כ ל מ נ ח
dx+dy–cdt+dz dy+dz–cdt+dx dz–cdt+dy+dx dx+dy+dz–cdt dx+dz+dy–cdt dy–cdt+dx+dz –cdt+dz+dx+dy
–dx–dy+cdt–dz –dy–dz+cdt–dx –dz+cdt–dy–dx –dx–dy–dz+cdt –dx–dz–dy+cdt –dy+cdt–dx–dz cdt–dz–dx–dy
H V I H' V H' I H H' I V H H V H' I H H' V I V I H H' I H' H V
ס ע פ צ ק ר ש
dz–cdt+dx+dy
–dz+cdt–dx–dy
H' I H V
ת(16.10)
Сумма каждой пары 22 линейных форм (16.10) удовлетворяют «вакуумному условию», например,
(dz–cdt+dx+dy) + (–dz+cdt–dx–dy) = 0. (16.11)
Представим линейные формы (16.8) и (16.9) в виде комплексно сопряженной пары аффинных агрегатов
ds = lсdt + idx + jdy + kdz, (16.12)
ds* = lсdt – idx – jdy – kdz , (16.13)
| l | i | j | k | |
| l | –1 | –1 | –1 | –1 |
| i | –1 | –1 | k | –j |
| j | –1 | –k | –1 | i |
| k | –1 | j | –i | –1 |
где k, j, i, l (H' V H I) – реперные единицы с одной из таблиц умножения типа:
| l | i | j | k | |
| l | –1 | –1 | –1 | |
| i | –1 | –1 | –k | –j |
| j | k | –1 | i | |
| k | –1 | j | –i | –1 |
| l | i | j | k | |
| l | –1 | |||
| i | –1 | k | –j | |
| j | –k | –1 | i | |
| k | j | –i | –1 |
Скалярное произведение аффинных агрегатов (16.12) и (16.13) приводит к квадратичной форме
dsds* = ds(+)2 = – с2 dt 2+ dx2+ dy 2 + dz 2, (16.14)
Аналогично из 22-х пар линейных форм (16.10) можно определить 22 пары комплексно сопряженных аффинных агрегатов и получить пары скалярных произведений, например,
(ldx–icdt+jdz+kdy) (–lcdt+idz+jdy+kdx) = nyudxydxu ссигнатурой (– + + –),(16.15)
(–ldx+icdt–jdz–kdy) (lcdt–idz–jdy–kdx) =–nyudxydxu ссигнатурой (+ – – +).
где
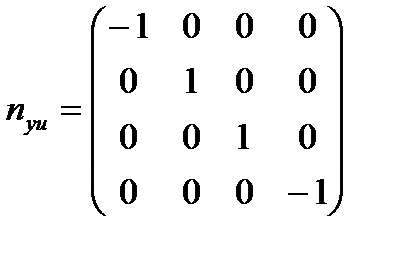. (16.16)
При этом соблюдается вакуумное условие
nyudxydxu + (– nyudxydxu) = 0 . (16.17)
Таким образом, из 22 пар световых линейных форм (или аффинных агрегатов) – «Букв Иврита» (16.10), посредством их скалярного произведения составляются 462 метрики (суть «Двухбуквенные комбинации»). Половина из них – это перевернутые комбинации тех же «Букв», например, לא и אל, מב и מב, и т.д. Число таких неповторяющихся парных соединений (скалярных произведений) равно 462 : 2 = 231 (א” רל). Это число сочетаний 22-х символов по 2:
.
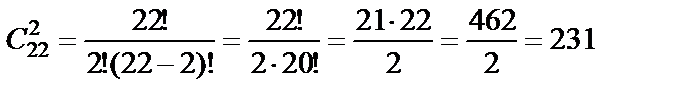| Рис. 16.1. Попытка проиллюстрировать одну из возможных реализаций световой ткани (рисунок Лебедева - Прохорова), сотканной из 462 световых «нитей» (лучей) и «антинитей» (антилучей) |
Раби Мойша Кардоверо (РаМаК) в книге «ПаРДеС Риманим» отметил, что еще есть под-Ткань, составленная из всевозможных аналогичных перестановок 3-х букв Иврита (Лашон а-Койдеш – Святого Языка). Под ней Ткань, составленная из различных комбинаций (перестановок) 4-х букв Иврита, и т.д. до самой «плотной» Ткани составленной из всевозможных перестановок 620-и букв Иврита. Число комбинаций этой под-под-….-под-Ткани для нас соответствует Бесконечности.
Но как бы не была сложна многослойная Исходная Ткань Бытия, в Ней постоянно повторяется структура Древа Жизни (Сфирот):
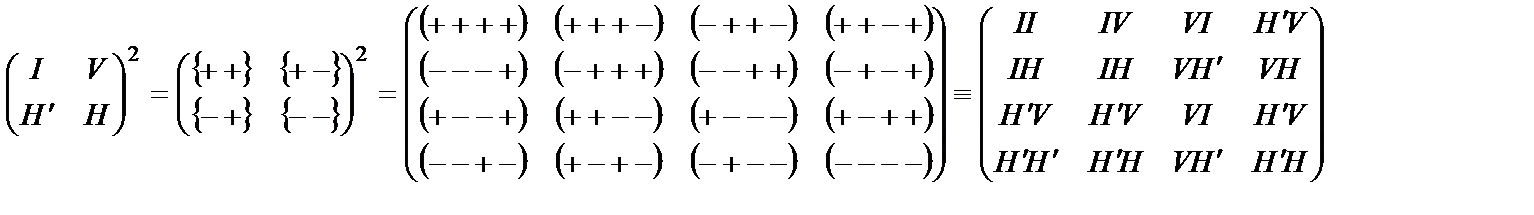(16.18)
– Основного варианта Раскрытия Великого Имени ה-ו-ה-י (Йюд - Г’ей - Вав - Г’ей) = H’V H I,
(коц) II – Кетер (1 Сфира)
יHH – Хохма (2 Сфира)
הVV – Бина (3 Сфира)
וIV, IH, IH¢, VH, VH¢, HH¢ – Заир Ампин
VI, HI, H¢I, HV, H¢V, H¢H (6 сдвоенных Сфирот)
הH¢H¢ – Малхут (10 Сфира) (16.19)
которая содержит в себе Потенцию Раскрытия Вселенского Человека (рис. 16.2)
| 02 = 20 1 |
| 01 = 10 |
| 12 = 21 |
| 13 = 31 |
| 03 = 30 |
| 32 =32 |
 |
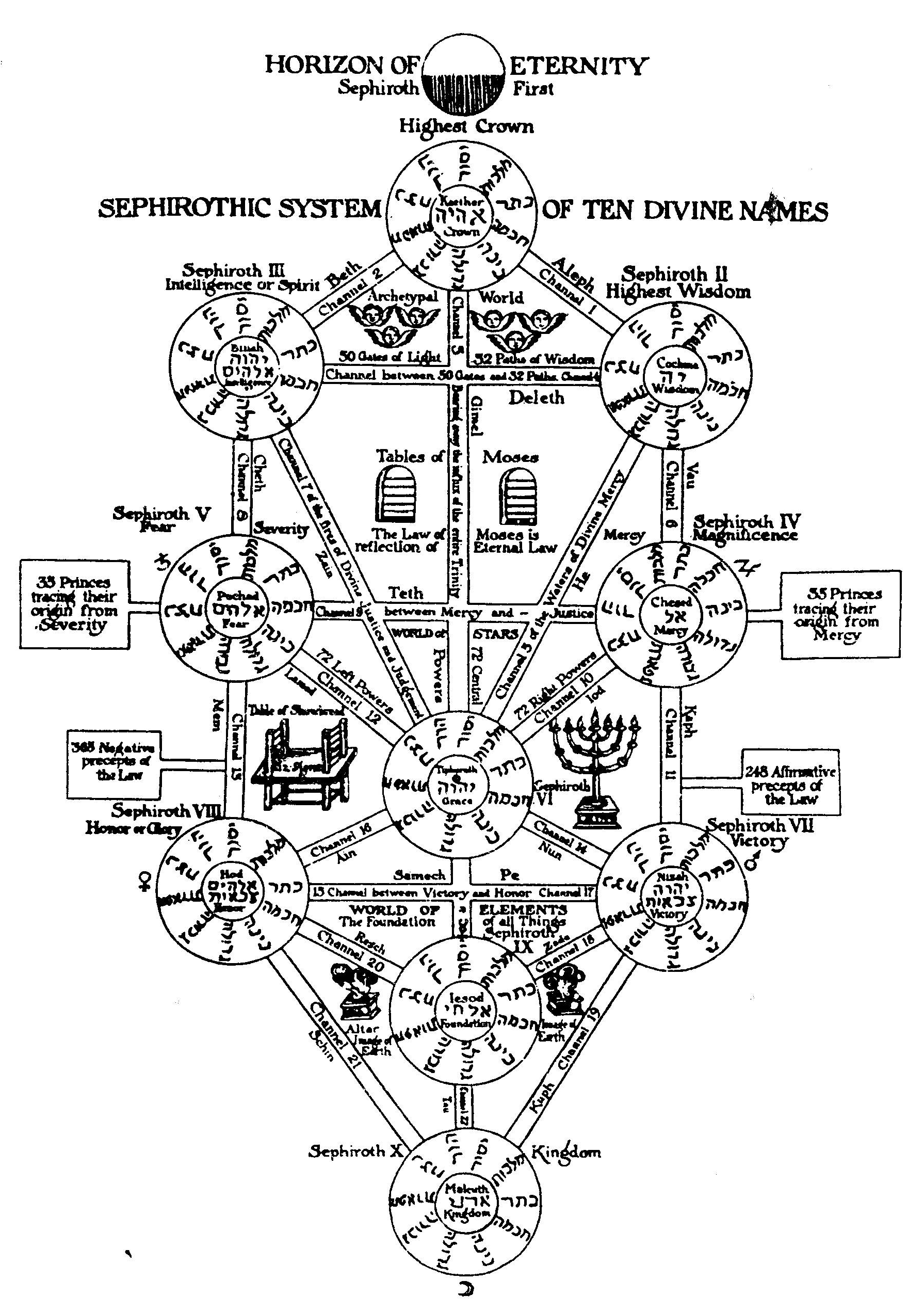Рис. 16.2. Раскрытое Древо Жизни (или Древо Сфирот)
имеет структуру Человека. Здесь:
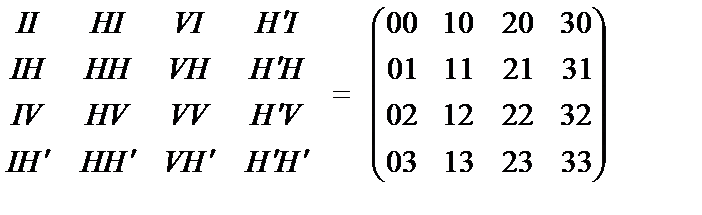
где
II = 00 – Кетер; i
HH = 11 – Хохма; I
VV = 22 – Бина; H
= 
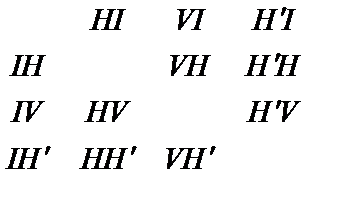– Тиферет*; V
H'H' = 33 – Малхут. H¢
(16.20)
Поэтому Исходная Световая Ткань Бытия изначально содержит в себе Потенцию Раскрытия Эмбриона Вселенского Человека (рис. 16.3) .
Рис. 16.3 Развитие Эмбриона Вселенского Человека, Имя Которого
ה-ו-ה-י (Йюд-Г’ей-Вав-Г’ей) = H’V H I