Второй этап компактификации дополнительных измерений.

«Вакуумный баланс» и «вакуумное условие»

На втором этапе компактификации дополнительных измерений определим аддитивную суперпозицию всех 16 метрик (11.1)

ds_S² = ds^{(+– – –)2} + ds^{(+ + + +)2} + ds^{(– – – +)2} + ds^{(+ – – +)2} +

+ ds^{(– – + –)2} + ds^{(+ + – –)2} + ds^{(– + – –)2} + ds^{(+ – + –)2} +

+ ds^{(– + + +)2} + ds^{(– – – – )2} + ds^{(+ + + –)2} + ds ^{(– + + –)2} +

+ ds^{(+ + – +)2} + ds^{(– – + +)2} + ds^{(+ – + +)2} + ds^{(– + – +)2} = 0 (12.1)

Действительно, складывая метрики (11.1), получим

ds_S² = (dx₀dx₀ – dx₁dx₁ – dx₂dx₂ – dx₃dx₃) + (dx₀dx₀ + dx₁dx₁ + dx₂dx₂ + dx₃dx₃) +

+ (– dx₀dx₀ – dx₁dx₁ + dx₂dx₂ – dx₃dx₃) + (dx₀dx₀ – dx₁dx₁ – dx₂dx₂ + dx₃dx₃) +

+ (– dx₀dx₀ – dx₁dx₁ + dx₂dx₂ – dx₃dx₃) + (dx₀dx₀ + dx₁dx₁ – dx₂dx₂ – dx₃dx₃) +

+ (– dx₀dx₀ + dx₁dx₁ – dx₂dx₂ – dx₃dx₃) + (dx₀dx₀ – dx₁dx₁ + dx₂dx₂ – dx₃dx₃ ) + (12.2)

+ (– dx₀dx₀ + dx₁dx₁ + dx₂dx₂ + dx₃dx₃) + (– dx₀dx₀ –dx₁dx₁– dx₂dx₂ –dx₃dx₃) +

+ (dx₀dx₀ + dx₁dx₁ + dx₂dx₂ – dx₃dx₃) + (– dx₀dx₀ +dx₁dx₁ +dx₂dx₂ – dx₃dx₃) +

+ (dx₀dx₀ + dx₁dx₁ – dx₂dx₂ + dx₃dx₃) + (– dx₀dx₀ – dx₁dx₁+ dx₂dx₂ +dx₃dx₃) +

+ (dx₀dx₀ – dx₁dx₁ + dx₂dx₂ + dx₃dx₃) + (– dx₀dx₀ + dx₁dx₁ – dx₂dx₂ + dx₃dx₃) = 0.

Вместо суммирования однородных слагаемых в выражении (12.2), можно суммировать только знаки, стоящие перед этими слагаемыми. Поэтому для сокращения записей выражение (12.2) можно представить в эквивалентном ранжирном виде:

0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 =

( 0 0 0 0) (+ + + +) (– – – + ) (+ – – + ) (– – + – ) (+ + – – ) (– + – – ) (+ – + – ) (– + + +) (0 0 0 0) +

+ + + + + + + + + +

(0 0 0 0) (– – – – ) (+ + + – ) (– + + – ) (+ + – +) (– – + +) (+ – + +) (– + – +) (+ – – –) (0 0 0 0) +

= 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 .

(12.3)

Сумма знаков, как по столбцам ранжиров (12.3), так и по их строкам между ранжирами, равна нулю.

Ранжирное тождество (12.3) будем называть поперечно «расщепленным нулем», положенным в основание геометрофизики l_m¸n-вакуума.

В каждой точке «вакуума» имеется бесконечное количество поперечно «расщепленных нулей», соответствующих каждому l_m¸n-вакууму (рис. 12.1).

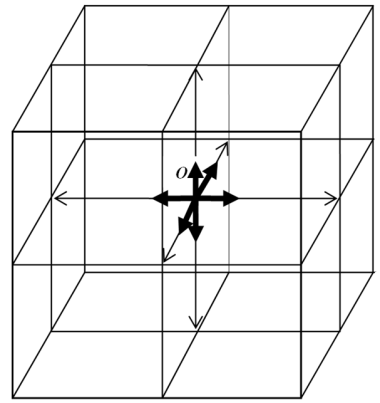
Рис. 12.1. В каждой точке О «вакуума» имеет место бесконечное количество

поперечно «расщепленных нулей» каждого l_m¸n-вакуума (т.е. продольного 3-мерного слоя)

Продольно и поперечно «расщепленный ноль» в точке О «вакуума» таит в себе образ евангелического крещения. Ортогональные Декартовы перекладины, на которых был распят Спаситель, легли в основу всей современной науки.

Рис. 12.2. Одна из реализаций двухмерной проекции трехмерной визуализации локального участка 10-мерного многообразия Калаби-Яу [24]

Определение № 12.1Поперечно «расщепленный ноль» – определен в каждой точке l_m¸n-вакуума ранжирным выражением (12.3).

Определение № 12.2Продольно «расщепленный ноль» – определен в каждой точке «вакуума» как полная совокупность поперечно «расщепленных нулей» всех l_m¸n-вакуумов.

Сложение (усреднение) шестнадцати метрических пространств с различными сигнатурами (топологиями) (12.1) приводит к Риччи-плоскому пространству, во многом схожему с 10-мерным многообразием Калаби-Яу (рис. 12.2), которое используется в теории суперструн.

Второй этап компактификации дополнительных (математических) измерений привел к полному их сокращению. Вместе с тем ранжирное выражение (12.3) является математической формулировкой «вакуумного баланса».

Определение № 12.3 «l_m¸n-вакуумный баланс» (или «вакуумный баланс») – это утверждение, что каждая точка l_m¸n-вакуума («вакуума») сбалансирована относительно «расщепленного нуля» вида (12.3). То есть в каждой точке l_m¸n-вакуума («вакуума») изначально задан продольно и поперечно «расщепленный нуль», любые отклонения от которого связаны с возникновением взаимно противоположных проявлений.

Одной из основных аксиом Алгебры сигнатур является утверждение, что никакие действия с l_m¸n-вакуумом не могут привести к глобальному устойчивому нарушению «l_m¸n - вакуумного баланса» (12.3). Поэтому «l_m¸n-вакуумный баланс» лежит в основе «l_m¸n-вакуумного условия».

Определение № 12.4«l_m¸n-вакуумное условие» (или «вакуумное условие») – любые проявления в l_m¸n-вакууме («вакууме») должны носить взаимно противоположный характер: волна – антиволна, выпуклость – вогнутость, движение – антидвижение, сжатие – растяжение и т.д.». Локальные l_m¸n-вакуумные («вакуумные») сущности и антисущности могут быть сдвинуты и повернуты относительно друг друга, но в среднем по всей l_m¸n - вакуумной области они полностью компенсируют проявления друг друга, восстанавливая «l_m¸n - вакуумный баланс» («вакуумный баланс»).

На основании вакуумного условия можно дать следующее определение «вакууму».

Определение № 12.5«Вакуум» – это полный инвариант для любых видов пространственных и пространственно-временных преобразований. То есть, какие бы взаимно - противоположные изменения не происходили, в среднем «вакуум» всегда остается неизменным.

Ранжирное выражение (12.3) позволяет проделывать в окрестности «пустотой» точки О некоторые операции без нарушения «вакуумного баланса». К таким операциям относится, например, симметричный перенос первых столбцов с инвертированием знаков:

0 = – = + = – = + = – = + = – = + = 0 =

(0 0 0) ( + + + ) ( – – + ) ( – – + ) ( – + – ) ( + – – ) ( + – – ) ( – + – ) ( + + +) (0 0 0 ) +

+ + + + + + + + + +

(0 0 0) (– – – ) (+ + – ) (+ + –) (+ – +) (– + +) (– + +) (+ – +) (– – – ) (0 0 0)+

= 0 = + = – = + = – = + = – = + = – = 0

(12.4)

или перенос любой из строк из числителей ранжиров (12.3) в их знаменатель, также с инвертированием знаков, например:

0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 =

(0 0 0 0 ) (+ + + + ) (– – – + ) (+ – – + ) (+ + – – ) (– + – – ) (+ – + – ) (– + + +) (+ + – +)+

+ + + + + + + + +

(0 0 0 0) (– – – – ) (+ + + – ) (– + + – ) (– – + +) (+ – + +) (– + – +) (+ – – –) (– – + –)+

= 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0

(12.5)

Раби Мойша Кардоверо (РаМаК) в книге «ПаРДеС Риманим» отметил, что мекубалим (каббалисты – мудрецы Тайной ТОРЫ) часто символизировали Древо Сфирот буквой א (Алеф), которая состоит из трех букв

א(Алеф) ^ºי ו י (12.6a)

Гематрия (числовое значение) буквы Алеф совпадает с гематрией Четырехбуквенного Имени ТВОРЦА (9.6a)

אºי ו י= 10 + 6 + 10 = 10 + 16 = 26, (12.6b)

ה-ו-ה-י = 5 + 6 + 5 + 10 = 26.

Матрица сигнатур (11.5)

,

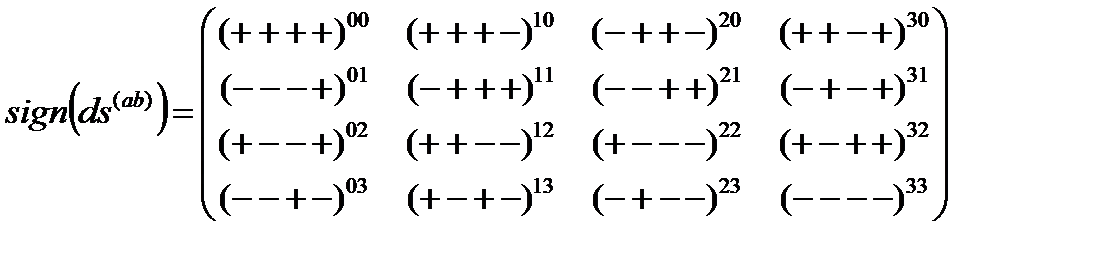удивительно точно соответствует структуре буквы א Алеф (12.6a) во многих аспектах.

Во-первых, в букве א упакованы две матицы стигнатцр

ו י= 6 + 10 = 16, י ו= 10 + 6 + 10 = 16, 16 + 16 = 32.

Во-вторых, антисимметричные свойства матрицы сигнатур относительно главной диагонали соответствует антисимметричному расположению двух букв י (Йюд) относительно буквы ו (Вав) в букве א (Алеф) и т.д.

Данные обстоятельства еще раз подтверждают, что матрицы стигнатур (8.2) и сигнатур (11.5) могут быть интерпретированы, как проекции свойств каббалистического Древа Сфирот на метрические свойства «вакуума»(l_m¸n -вакуума). И Имя ВСЕВЫШНЕГО ה-ו-ה-י (H¢ V H I i) Благословенно в каждом месте Пребывания ЕГО.

13. Двусторонняя l_m¸n-вакуумная протяженность

Вакуумный баланс не нарушается, если в ранжирах (12.3) перевести одну строчку из числителя в знаменатель с изменением знаков на противоположные по правилам арифметики. Например, перенесем нижние сигнатуры (– + + +) и (+ – – –) из числителей ранжиров (12,3) в их знаменатели

(+ + + +) (– – – + ) (+ – – + ) (– – + – ) (+ + – – ) (– + – – ) (+ – + – ) (+ – – – )+

+ + + + + + + +

(– – – – ) (+ + + – ) (– + + – ) (+ + – +) (– – + +) (+ – + +) (– + – +) (– + + +)+

=0 =0 =0 =0 =0 =0 =0 =0 .

(13.1)

В этом случае в знаменателе левого ранжира (13.1) получилась сигнатура пространства Минковского (+ – – –) с метрикой (7.3)

ds^{(+ – – –)2} = c²dt² – dx² – dy² – dz² = dx₀² – dx₁² – dx₂² – dx₃² = 0 , (13.2)

а в знаменателе правого ранжира (13.1) – инвертированная сигнатура антипространства Минковского (– + + +) с метрикой (7.4)

ds^{(– + + +)2} = – c²dt² + dx² + dy² + dz² = – dx₀² + dx₁² + dx₂² + dx₃² = 0. (13.3)

Таким образом, посредством сложения (или арифметического усреднения) семи метрик с сигнатурами в числителе левого ранжира (13.1) можно, согласно определению № 7.2, выделить «внешнюю» сторону 2³-l_m¸n -вакуумной протяженности с сигнатурой (+ – – –), или «субконт»; а посредством сложения (или арифметического усреднения) семи метрик с сигнатурами в числителе правого ранжира (13.1) можно, выделить «внутреннюю» сторону 2³-l_m¸n -вакуумной протяженности с сигнатурой (– + + +), или «антисубконт».

При этом удается понизить число рассматриваемых измерений до 4+4=8 и сохранить вакуумный баланс

ds^{(+ – – –)2} + ds^{(– + + +)2} = 0 или (+ – – –) + (– + + +) = (0 0 0 0). (13.4)

Как было показано в п. 7, данный результат можно интерпретировать как наличие у 2³-l_m¸n -вакуумной протяженности двух взаимно-противоположных 4-мерных сторон:

- «внешней стороны» с метрикой ds^{(+ – – –)2}, с условным названием «субконт» (опр. № 7.4);

- «внутренней стороны» с сопряженной метрикой ds^{(– + + +)2}, с условным названием

«антисубконт» (опр. № 7.5).

В любой светогеометрической задаче следует иметь в виду, что l_m¸n-вакуумная протяженность является результатом аддитивного наложения (усреднения) минимум шестнадцати 4-мерных протяженностей с метриками (11.1) и сигнатурами (топологиями) (11.5). То есть минимум математических измерений должно быть 4 × 16 = 64. Однако в ряде задач модель «вакуума» может быть сведена к двухстороннему рассмотрению с 4 + 4 = 8 - мерной l_m¸n-вакуумной протяженностью.

Переход от 64 (или 8) математических измерений к трем физическим измерениям «вакуума» и одному временному измерению «стороннего наблюдателя» будет рассмотрен ниже.

Односторонне рассмотрение 4-мерной l_m¸n-вакуумной протяженности в Алгебре сигнатур (Алсигне) запрещено «вакуумным условием». Это значительно отличает Алсигну от ОТО А. Эйнштейна.

Итак, выяснилось, что пространство Минковского с сигнатурой (+ – – –) может быть представлено в виде суммы (т.е. аддитивного наложения или усреднения) 7-и метрических протяженностей с сигнатурами из числителя левого ранжира (13.1)

ds ^{(+ – – –)2} = ds^{(+ + + +)2} + ds^{(– – – +)2} + ds^{(+ – – +)2} + ds^{(– – + –)2} + (13.5)

+ ds^{(+ + – –)2} + ds ^{(– + – –)2} + ds^{(+ – + –)2},

а антипространство Минковского с сигнатурой (– + + +) может быть представлено в виде суммы 7-и метрических протяженностей с сигнатурами из числителя правого ранжира (13.1)

ds^{(– + + +)2} = ds^{(– – – – )2} + ds^{(+ + + –)2} + ds^{(– + + –)2} + ds^{(+ + – +)2} + (13.6)

+ ds^{(– – + +)2} + ds^{(+ – + +)2} + ds^{(– + – +)2}.

В развернутом виде суммарные метрики (13.5) и (13.6) имеют вид соответствующий ранжирам (13.1). (13.7)

d сигнатурами.ких протяженностей с различными сигнатурами.s(+ + + +)2 = dx02 + dx12 + dx22 + dx32 ds(– – – +)2 = – dx02 – dx12 – dx22 + dx32 ds(+ – – +)2 = dx02 – dx12 – dx22 + dx32 ds(– – + –)2 = – dx02 – dx12 + dx22 – dx32 ds(– + – –)2 = – dx02 + dx12 – dx22 – dx32 ds(+ – + –)2 = dx02 – dx12 + dx22 – dx32 ds(+ + – –)2 = dx02 + dx12 – dx22 – dx32 ds(+– – –)2 = dx02 – dx12 – dx22 – dx32

ds(– – – – )2 = – dx02 – dx12 – dx22 – dx32 ds(+ + + –)2 = dx02 + dx12 + dx22 – dx32 ds (– + + –)2 = – dx02 + dx12 + dx22 – dx32 ds(+ + – +)2 = dx02 + dx12 – dx22 + dx32 ds(+ – + +)2 = dx02 – dx12+ dx22 + dx32 ds(– + – +)2 = – dx02 + dx12 – dx22 + dx32 ds(– – + +)2 = – dx02 – dx12 + dx22 + dx32 ds(– + + +)2 = – dx02 +d x12 + dx22 + dx32