Одномерный классический гармонический осциллятор

Колебаниями называются процессы, отличающиеся той или иной степенью повторяемости. В зависимости от физической природы повторяющегося процесса различают колебания: механические, электромагнитные, электромеханические и т.д. Рассмотрим механические колебания.

В зависимости от характера воздействия на колеблющуюся систему различают свободные (или собственные) колебания, вынужденные колебания, автоколебания и параметрические колебания.

Силу, под действием которой происходит колебательный процесс, называют возвращающей силой, так как она стремится вернуть тело или материальную точку в положение равновесия.

Свободные колебания совершаются системой, выведенной из положения равновесия.

Собственныминазываются свободные колебания без учёта сил сопротивления (без затухания).

Вынужденныминазываются такие колебания, в процессе которых колеблющаяся система подвергается воздействию внешней периодически изменяющейся силы. Примером служат колебания моста, возникающие при прохождении по нему людей, шагающих в ногу.

Автоколебания, как и вынужденные колебания, сопровождаются воздействием на колеблющуюся систему внешних сил, однако моменты времени, когда осуществляются эти воздействия, задаются самой колеблющейся системой – система сама управляет внешним воздействием. Примером автоколебательной системы являются часы, в которых маятник получает толчки за счёт энергии поднятой гири или закрученной пружины, причем эти толчки происходят в моменты прохождения маятника через среднее положение.

При параметрических колебаниях за счёт внешнего воздействия происходит периодическое изменение какого-либо параметра системы, например, длины нити, к которой подвешен шарик, совершающий колебания.

Простейшими являются гармонические колебания, при которых колеблющаяся величина (например, отклонение маятника) изменяется со временем по закону синуса или косинуса. Этот вид колебаний особенно важен по следующим причинам: во-первых, колебания в природе и в технике часто имеют характер, очень близкий к гармоническому, во-вторых, периодические процессы иной формы (с другой зависимостью от времени) могут быть представлены как наложение нескольких гармонических колебаний. Гармонические колебания удобно представить в виде круговой диаграммы (рис.1). Пусть точка 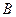движется по окружности радиусом 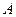. Её положение задаётся радиус-вектором 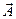. Положение равновесия задаётся точкой 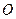. Радиус-вектор 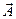равномерно вращается с угловой скоростью 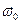. Проекции радиус-вектора 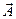на оси 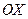или задаются математическими выражениями (уравнениями) гармонических колебаний:

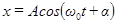(1)

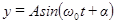(2)

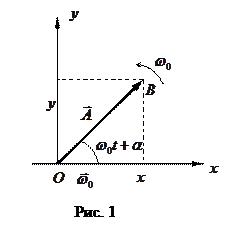Мы будем использовать уравнение гармонических колебаний в виде (1). Координата 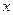задаёт значение колеблющейся величины. Величина 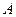– амплитуда колебаний, т.е. максимальное отклонение колеблющейся точки от положения равновесия. Величина 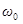, равная числу колебаний за время 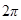секунды, называется циклической частотой. Аргумент косинуса 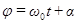, характеризующий значение колеблющейся величины в момент времени 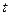, называется фазойколебаний. Фаза колебаний 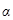, соответствующая начальному моменту времени, называется начальной фазой колебаний. Время одного полного колебания 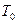называется периодом колебаний. Число колебаний 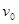за время, равное одной секунде, называется частотойколебаний.

.

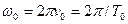Скорость колеблющейся точки находится дифференцированием выражения (1) по времени:

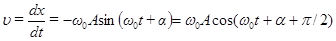(3)

Дифференцируя вторично, получаем ускорение:

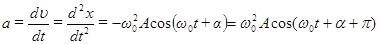. (4)

.

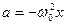На рис. 2 представлены зависимости 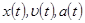. Скорость опережает смещение на 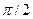, ускорение находится в противофазе по отношению к смещению.

Каждое конкретное колебание характеризуется определенным значением амплитуды 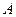и начальной фазы 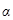. Определим их значения из начальных условий 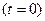. В этом случае 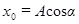, 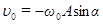. Отсюда следует, что

, .

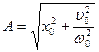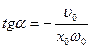Выведем дифференциальное уравнение гармонических колебаний. Из выражения (4) следует, что

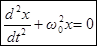или . (5)

Уравнение (5) является дифференциальным уравнением гармонических колебаний. Это уравнение является общим уравнением, описывающим гармонические колебания. Его решением являются функции (1) или (2). Следовательно, можно сказать, что гармоническиминазываются колебания, совершаемые по закону синуса или косинуса.

Колебательные системы, описываемые уравнением (5) называются одномерным классическим гармоническим осциллятором.Модель одномерного классического гармонического осциллятора оказывается справедливой не только для механических, но и других видов собственных незатухающих колебаний. В различных разделах физики используется единый математический язык описания гармонических колебаний.

Рассмотрим конкретные примеры гармонических осцилляторов в механике.

Пружинный маятник (рис. 3)

Применим к движению груза на пружине второй закон Ньютона: 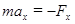, где 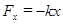- сила упругости: ,

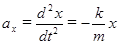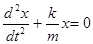. (6)

Сравнивая (5) и (6), получаем:

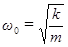(7)

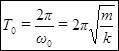(8)

Мы нашли собственную циклическую частоту (7) и период колебаний (8) груза на пружине.

Физический маятник (рис. 4)

Физическим маятником называется твердое тело, колеблющееся относительно неподвижной горизонтальной оси (оси подвеса), не проходящей через центр тяжести. При небольших углах отклонения ( 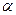-мал) физический маятник совершает гармонические колебания. Сила, возвращающая маятник в положение равновесия, представляет собой составляющую силы тяжести, приложенную в точке :

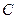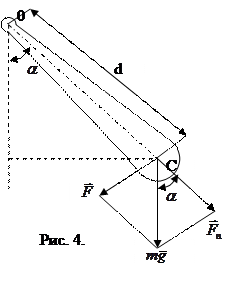
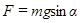
Момент этой силы относительно оси 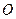равен:

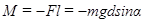, где 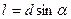- плечо силы 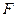относительно оси 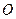, знак минус соответствует тому, что момент 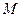стремится вернуть маятник в положение равновесия, аналогично квазиупругой силе.

В соответствии с уравнением динамики вращательного движения

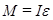, где 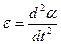- угловое ускорение, 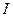- момент инерции маятника относительно оси О. Получаем

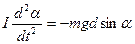. (9)

Ограничившись малыми колебаниями 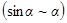, после преобразований получаем уравнение (9) в виде:

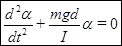(10).

Сравнив выражения (5) и (10) мы видим их математическую аналогию, что позволяет записать выражения для циклической частоты и периода колебаний физического маятника:

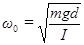(11)

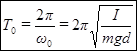, (12)

где 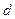-расстояние от центра тяжести до оси вращения.

Если период колебаний не зависит от амплитуды, то такие колебания называются изохронными. Мы видим, что малые колебания физического маятника изохронны. Колебания приближенно изохронны, когда угловая амплитуда колебаний не превышает нескольких градусов. При больших амплитудах изохронность нарушается. На свойстве изохронности колебаний маятника основано его применение в часах.

Математический маятник (рис. 5)

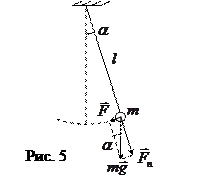Математический маятник является частным случаем физического маятника. Математическим маятником называют идеализированную систему, состоящую из невесомой и нерастяжимой нити, к которой подвешена масса, сосредоточенная в одной точке. Примером математического маятника может служить шарик, подвешенный на длинной нити. В случае математического маятника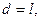 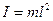,где 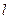-длина математического маятника. Тогда формулы (11) и (12) запишутся в виде:

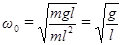(13)

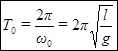(14)

Сравнивая формулы (12) и (14), заключаем, что физический маятник колеблется с периодом математического маятника, длина которого

,

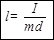называется приведенной длиной физического маятника.

Сложение колебаний

Векторная диаграмма

Гармонические колебания удобно представлять в виде векторных (круговых) диаграмм. В этом случае гармоническое колебание совершает проекция радиус-вектора, равного по модулю амплитуде колебаний .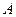

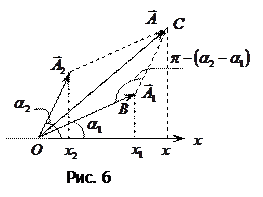Воспользуемся методом векторных диаграмм при сложении гармонических колебаний одинакового направления с одинаковыми частотами. Смещение 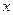колеблющегося тела равно сумме смещени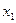й и 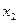, которые записываются следующим образом:

и (16)

Представим оба колебания с помощью векторов 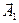и 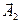(рис. 6). Построим по правилам сложения векторов результирующий вектор 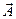. Легко видеть, что проекция этого вектора на ось 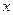равна сумме проекций слагаемых векторов 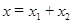. Следовательно, проекция вектора 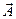представляет собой результирующее колебание.

Этот вектор вращается с той же угловой скоростью (циклической частотой) 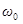, как и векторы 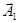и 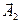, так что результирующее движение будет гармоническим колебанием с частотой 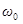, амплитудой 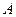и начальной фазой 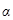. Из построения видно, что

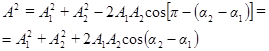(17)

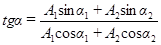. (18)

Итак, представление гармонических колебаний посредством векторов дает возможность свести сложение нескольких колебаний к операции сложения вращающихся векторов.

Проанализируем выражение (17) для амплитуды:

а) если разность фаз колебаний 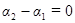, т.е. колебания происходят в одинаковой фазе, то амплитуда результирующего колебания равна ;

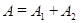б) если разность фаз колебаний 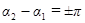, т.е. колебания находятся в противофазе, то амплитуда результирующего колебания .

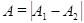Биения

Особый интерес представляет случай, когда два складываемых колебания одинакового направления малоотличаются по частоте. Результирующее движение при этих условиях можно рассматривать как гармоническое колебание с пульсирующей амплитудой. Такое колебание называется биением.

Пусть частота одного колебания 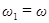, а частота второго колебания 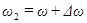, причем, . Амплитуды обоих колебаний полагаем одинаковыми и равными 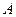. Для упрощения расчетов полагаем начальные фазы колебаний равными нулю. Тогда уравнения складываемых колебаний будут иметь следующий вид:

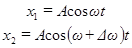
Складывая эти выражения и применяя тригонометрическую формулу для суммы косинусов 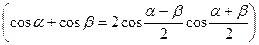, получаем 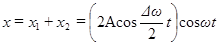(19).

(во втором множителе пренебрегли членом 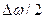по сравнению с ).

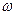График функции (19) для случая 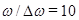изображен на рисунке 7.а.

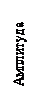
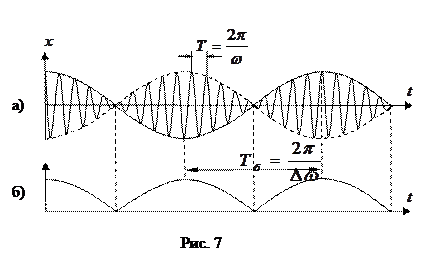Заключенный в скобки множитель в формуле (19) изменяется гораздо медленнее, чем второй множитель, так как . Это дает нам основание рассматривать колебание (19) как гармоническое колебание частоты 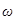, амплитуда которого изменяется по некоторому закону. Выражением этого закона не может быть множитель, стоящий в скобках, так как он изменяется от 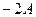до 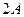, в то время, как амплитуда по определению – величина положительная. График амплитуды показан на рис 7.б. Аналитическое выражение амплитуды, очевидно, имеет вид:

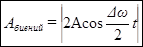. (20)

Функция (20) – периодическая функция с частотой в два раза превышающей частоту выражения, стоящего под знаком модуля, т.е. с частотой 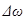. Заменяя в выражении (19) амплитуду через значение (20), получаем уравнение биений:

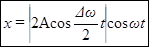(21)