Если система сил имеет равнодействующую, то момент равнодействующей относительно произвольно выбранной точки равен сумме моментов всех сил системы относительно этой точки.

Основные свойства пары сил

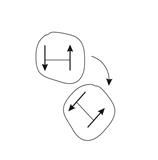
В соответствии с теоремой об эквивалентности систем сил, две пары сил эквивалентны тогда и только тогда, когда равны их моменты. Отсюда следует, что, не изменяя действия пары сил на абсолютно твёрдое тело, можно производить следующие преобразования пар сил (Рис. 2.4 – 2.6):

1. переносить и поворачивать пару сил в плоскости её действия;

2. переносить пару сил в любую плоскость, параллельную плоскости

действия пары сил;

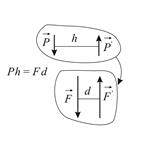
3. изменять плечо и модули сил, образующих пару, так чтобы модуль

момента пары оставался неизменным.

Рис. 2.4		Рис. 2.5		Рис. 2.6

Доказанная ранее теорема о сложении пар оказывается справедливой при произвольном расположении пар сил в пространстве, поскольку в случае параллельности плоскостей действия, пары сил можно перенести в одну плоскость.

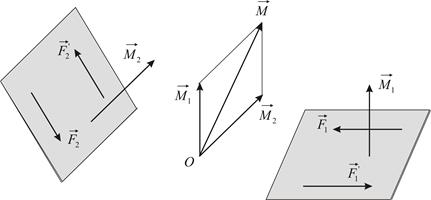Рис. 2.7

Таким образом,

Две произвольно расположенные пары сил эквивалентны одной паре сил, момент которой равен сумме моментов слагаемых пар сил.

ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ

1. Сформулировать необходимые и достаточные условия равновесия системы сил.
2. Сформулировать необходимые и достаточные условия эквивалентности систем сил.
3. Сформулировать необходимые и достаточные условия эквивалентности пар сил.
4. Как можно видоизменять пару сил, не изменяя её действие на абсолютно твёрдое тело?
5. Сформулировать теорему Вариньона.

ЛЕКЦИЯ 4

ОБЪЁМНЫЕ И ПОВЕРХНОСТНЫЕ СИЛЫ

До сих пор мы оперировали так называемыми сосредоточенными силами, которые имеют определённую точку приложения (или линию действия). Сосредоточенная сила является одной из абстракций, используемых в механике. Реальные взаимодействия материальных тел всегда представляются распределёнными либо по объёму тела, либо по его поверхности. К поверхностным силам относятся силы давления, т.е. силы контактного действия, а к объёмным – гравитационные и электромагнитные силы. Сосредоточенные силы появляются в теории как равнодействующие поверхностных или объёмных сил.

Центр параллельных сил

При изучении объёмных и поверхностных сил широко используется центр параллельных сил. Это понятие вводится для системы параллельных сил, имеющих равнодействующую, причём точки приложения сил системы считаются фиксированными.

Центром параллельных сил называется точка, вокруг которой поворачивается равнодействующая системы параллельных сил при повороте всех сил системы вокруг своих точек приложения в одну и ту же сторону на один и тот же угол.

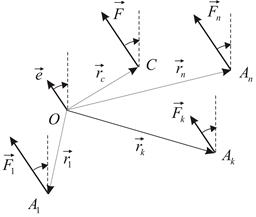Рис.3.1

Найдём положение центра параллельных сил 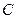для системы 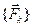, имеющей равнодействующую 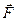. Пусть – единичный вектор, параллельный линиям действия сил системы (Рис. 3.1). Тогда 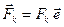, где 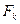– проекция силы на направление единичного вектора 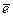. Для равнодействующей получаем:

Для любого центра 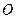, используя теорему Вариньона, получаем:

или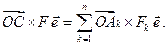

Вынося за скобку общий множитель 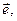получаем:

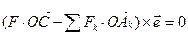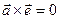или где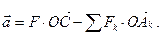

Векторное произведение равно нулю, если один из сомножителей равен нулю или если сомножители коллинеарны. Но Повернём все силы системы вокруг своих точек приложения в одну и ту же сторону на один и тот же угол (Рис. 3.1). Равнодействующая системы сил повернётся вокруг точки C в ту же сторону на тот же угол. Вместе с силами поворачивается вокруг точки O и вектор . В результате этой операции вектор изменил направление; вектор 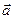остался неизменным, но по-прежнему 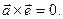Следовательно, 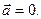т.е.

Отсюда

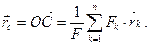(1)

Примем точку O за начало декартовой системы координат. Записывая формулу (1) в проекциях на координатные оси, получаем координаты центра параллельных сил:

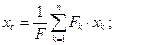
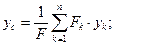
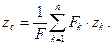
Центр тяжести