Физика конденсированного состояния
Физика конденсированного состояния
Рис. 2.7. Дифракция рентгеновских лучей в кристалле
В соответствии с рис. 2.7.
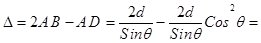
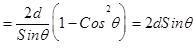 (2.8)
(2.8)
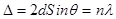 (2.9)
(2.9)
Узость рентгеновского луча, обусловленная малой диафрагмой, и большой размер зерна фотоэмульсии пленки, на которой наблюдаются условия дифракции, позволяют отказаться от фокусировки.
Измерив угол максимального отражения q, можно определить d для разных плоскостей, а по ним найти h k l:
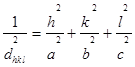 . (2.10)
. (2.10)
Для куба a = b = c:
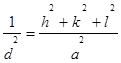 . (2.11)
. (2.11)
Дифракция на трехмерной решетке
Рассмотрим линейную цепочку атомов, образованную рядом одинаковых рассеивающих центров а вдоль линии АВ. Пусть она рассеивает монохроматическое излучение l.
Разность хода между соседними лучами (рис. 2.8)
 (максимум интерференции), h – целое
(максимум интерференции), h – целое


 (2.12)
(2.12)
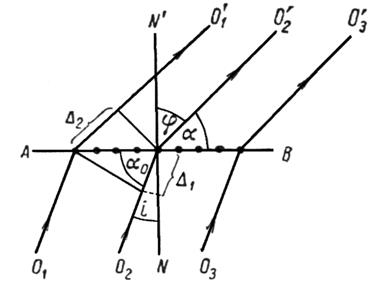
Рис. 2.8. Дифракция на линейной цепочке атомов
Постоянному значению угла a соответствуют лучи, расположенные вдоль образующих конуса с осью АВ и углом раствора 2a.
При дифракции на линейной решетке условия максимума образуют гиперболы на плоскости(рис. 2.9).
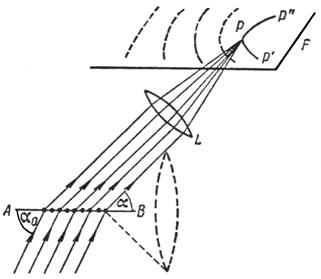
Рис. 2.9. Возникновение светлых линий P’PP’’ при дифракции от линейной решётки
При дифракции на двумерной решетке максимумы получатся только в тех направлениях, у которых оба угла a и b одновременно удовлетворяют условиям:
 (2.13)
(2.13)
Пересечения системы двух гипербол дадут систему светлых пятен (рис.2.10).
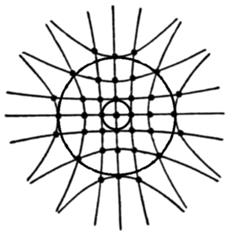
Рис. 2.10. Дифракция на двумерной и трехмерной решетках
Дифракция на трехмерной решетке (кристалл) дает максимумы при одновременном удовлетворении трех условий:
 (2.14)
(2.14)
Это три уравнения Лауэ, которые дополняются двумя геометрическими условиями:
 (2.15)
(2.15)
Уравнение Лауэ можно заменить одним интерференционным уравнением, позволяющим интерпретировать условия интерференции геометрически с помощью обратной решетки.
Вопрос – 5. Физическая природа упругой и пластической деформаций твердых тел.
Механическое напряжение и деформация
Под действием внешних сил в каждой точке твердого тела возникают механические напряжения.
Механическое напряжение численно равно силе, действующей на единицу площади.
Растянем силой  цилиндр площадью S (рис. 4.1)
цилиндр площадью S (рис. 4.1)
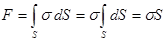 Þ
Þ 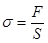 (4.1)
(4.1)
Размерность |s| = 1 Н/м2 = 1 Па (как и давление).
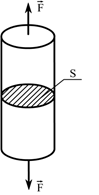
Рис. 4.1. К определению понятия механических напряжений
Деформация – это изменение формы или объема твердого тела без изменения его массы под действием внешней силы. При деформации меняется расстояние между какими-либо точками твердого тела. Виды деформации: растяжение, сжатие, сдвиг, кручение, изгиб.
При растяжении (рис. 4.4) относительная деформация исходного образца длиной lo (в процентах):
 , (4.3)
, (4.3)
где lk – конечная длина образца.
Диаграмма деформации для конкретного вещества отражает зависимость деформации e от приложенного напряжения s (рис. 4.5).

Рис. 4.5. Диаграмма деформации с площадкой текучести
Из диаграммы деформации e = f(s) можно узнать предел прочности твердого тела, области упругости, пластической деформации и др.
Участок ОА: упругая (обратимая) деформация (e << 1 %), область действия закона Гука; sу – предел упругости.
Участок АВ: пластическая (необратимая) деформация, после снятия напряжения размеры тела не восстанавливаются; sт – предел текучести.
Участок ВС – площадка текучести: деформация растет без значительного увеличения нагрузки; sп – предел прочности, образец разрушается
Рис. 4.8. Упругая сдвиговая деформация
Рис. 4.9. Двойникование при пластической деформации
При пластической деформации путем скольжения одна часть кристалла перемещается в направлении скольжения относительно другой вдоль плоскости скольжения (рис. 4.10).

Рис. 4.10. Пластическая деформация скольжением
Каждая решетка имеет несколько систем скольжения. Скольжение – процесс анизотропный и происходит не в направлении действующей силы, а по плоскости наибольшей плотности упаковки (с малыми индексами Миллера). Для ряда решеток (особенно металлов) расстояние между двумя соседними плотно упакованными плоскостями больше, чем между другими атомными плоскостями, поэтому для скольжения плотно упакованных плоскостей требуются минимальные сдвиговые усилия.
Направления скольжения также лежат в плотноупакованных плоскостях, так как в них требуются минимальные смещения между атомами. В каждой кристаллической решетке имеется несколько систем (плоскостей и направлений) скольжения. В ГЦК решетке минимальное межплоскостное расстояние между плоскостями{111} при a-параметре решетки равно  , а для менее плотно упакованных плоскостей {110}
, а для менее плотно упакованных плоскостей {110} 
Поляризация диэлектриков
Макроскопические характеристики поляризации
Из экспериментов (Фарадей) известно. что при заполнении диэлектриком конденсатора его емкость С возрастает в e раз (e – диэлектрическая проницаемость, зависящая от свойств диэлектрика).
 ;
;  Þ
Þ  , (13.5)
, (13.5)
т.е. увеличение емкости С конденсатора с диэлектриком в e означает, что разность потенциалов Vo уменьшается в e раз за счет поляризации диэлектрика. Заряды на поверхности диэлектрика нейтрализуют часть заряда конденсатора, что уменьшает поле в диэлектрике по сравнению с вакуумом (рис. 13.1).
Под действием внешнего электрического поля  в диэлектрике происходит ориентация электрических диполей, имеющих атомную или молекулярную природу, и возникает электрический (дипольный) момент, частично компенсирующий внешнее электрическое поле.
в диэлектрике происходит ориентация электрических диполей, имеющих атомную или молекулярную природу, и возникает электрический (дипольный) момент, частично компенсирующий внешнее электрическое поле.

Рис. 13.1. Поляризация диэлектрика в конденсаторе
Дипольный момент единицы объема вещества называется поляризуемостью.
 , (13.6)
, (13.6)
где  – элементарный электрический момент;
– элементарный электрический момент;
N – объемная плотность диполей.
Макроскопическими характеристиками поляризации являются также напряженность электрического поля в диэлектрике  и электрическая индукция
и электрическая индукция  . Векторы
. Векторы  ,
,  и
и  связаны соотношениями:
связаны соотношениями:
 (13.7)
(13.7)
 , (13.8)
, (13.8)
где  – поле в диэлектрике;
– поле в диэлектрике;
eо = 8,85×10–12 Ф/м.
Для большинства диэлектриков при не очень больших полях (< 106 В/м) величина e не зависит от  . Тогда из (13.7) и (13.8):
. Тогда из (13.7) и (13.8):
 , (13.9)
, (13.9)
где c = e – 1, – относительная диэлектрическая восприимчивость (чувствительность  к внешнему полю
к внешнему полю  ).
).
Пьезоэлектрики
В диэлектриках с нецентросимметричной структурой, кроме рассмотренных выше механизмов поляризации под действием  , возможна вынужденная поляризация под действием механического напряжения (пьезополяризация), температуры (пирополяризация), света (фотополяризация) и т.п.
, возможна вынужденная поляризация под действием механического напряжения (пьезополяризация), температуры (пирополяризация), света (фотополяризация) и т.п.
Поляризация под действием механического напряжения называется прямым пьезоэффектом. Пьезоэффект наблюдается во всех нецентросимметричных кристаллах (SiO2, A3B5, A2B6, KH2PO4 – KDP дигидрофосфат калия). Например, в ячейке кварца SiO2 без деформации дипольный момент равен нулю. При деформации возникает дипольный момент P = q×Dа (растяжение) и P = –q×Dа (сжатие) (рис. 13.11).
При сжатии кварца вдоль одной из осей второго порядка дипольный момент определяется соотношением:
P = d×s (13.40)
где d – пьезоэлектрический модуль, характеризующий эффективность деформации;
s – напряжение растяжения вдоль оси второго порядка.
В кристалле s – тензор второго ранга, а d – тензор третьего ранга. Вектор  имеет 3 компоненты: Рi, i=1, 2, 3.
имеет 3 компоненты: Рi, i=1, 2, 3.
Pi = dijk×sjk (13.41)

Рис. 13.11. Механизм пьезополяризации кварца при деформации: а) элементарная ячейка без деформации; б) ячейка растянута; в) ячейка сжата
Пьезоэлектрики на обратном и прямом пьезоэффекте используют как излучатели и приемники ультразвука (сонары), стабилизаторы частоты, электрические фильтры ВЧ и НЧ, в акустоэлектронике (ПАВ, линии задержки и т.п.) и не только в виде монокристаллов, но и в виде керамики и тонких пленок.
Сегнетоэлектрики
У некоторых диэлектриков наблюдается явление самопроизвольной поляризации с нелинейной зависимостью  (
(  ). Это сегнетоэлектрики, пример NaKC4H4О6×4H2O – сегнетова соль, BaTiO3 – титанат бария и другие.
). Это сегнетоэлектрики, пример NaKC4H4О6×4H2O – сегнетова соль, BaTiO3 – титанат бария и другие.
Поляризация сегнетоэлектриков характеризуется петлей гистерезиса (рис. 13.12), на которой есть точки остаточной поляризации PR и коэрцитивной силы Ес.

Рис. 13.12. Петля гистерезиса поляризации сегнетоэлектрика
Существование гистерезиса в сегнетоэлектриках обусловлено наличием сегнетоэлектрических доменов – объемных областей с одинаковой ориентацией дипольных моментов, но у соседних доменов векторы  противоположны (рис. 13.13).
противоположны (рис. 13.13).
Причина возникновения доменов – сильное взаимодействие между соседними диполями в кристалле, приводящее к их упорядочению, даже в макроскопических областях.
Домены разделены границами, которые характеризуют по направлению  : 180°-домены, если
: 180°-домены, если  и
и  противоположны, или 90°-домены, когда
противоположны, или 90°-домены, когда  ^
^  . Толщина границы £ 10
. Толщина границы £ 10  , но ее энергия довольно велика (~10–6 Дж/см2).
, но ее энергия довольно велика (~10–6 Дж/см2).

Рис. 13.13. Деление сегнетоэлектрика на домены спонтанной поляризации
Поляризация сегнетоэлектрика может осуществляться за счет: 1) увеличения  каждого домена; 2) переориентации доменов; 3) увеличения некоторых доменов в объеме.
каждого домена; 2) переориентации доменов; 3) увеличения некоторых доменов в объеме.
Сегнетоэлектрики характеризуются дифференциальной относительной диэлектрической проницаемостью:
 , (13.42)
, (13.42)
которая зависит от Е.
С повышением температуры величина Р уменьшается и при ТКюри тепло разрушает домены и сегнетоэлектрик становится параэлектриком. В параэлектрической области работает закон Кюри-Вейсса:
 (13.43)
(13.43)
Сегнетоэлектрики используются в микроэлектронике как высокоэффективные диэлектрики для конденсаторов повышенной емкости, а также как элементы памяти.
Классификация магнетиков
Основная характеристика магнетика – это намагниченность  – магнитный момент единицы объема вещества:
– магнитный момент единицы объема вещества: 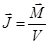 , который изменяется с увеличением
, который изменяется с увеличением  или
или  :
:
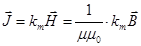 (14.1)
(14.1)
где m – относительная магнитная проницаемость вещества, т.е. во сколько раз  в веществе больше, чем в вакууме;
в веществе больше, чем в вакууме;
mо = 4p×10–7 Гн/м – магнитная постоянная.
km – магнитная восприимчивость (рис. 14.1).
km < 0 – диамагнетики
km > 0 – парамагнетики
Спонтанная намагниченность – ферромагнетики, km > 0 и нелинейно зависит от  .
.
Природа магнетизма обусловлена магнитными моментами ядер, электронных оболочек, молекул, дефектов. Возможно также индуцирование магнетизма внешним магнитным полем.

Рис. 14.1. Зависимость намагниченности J от внешнего поля Н для: 1 - парамагнетиков; 2 - диамагнетиков
Диамагнетики
В диамагнитных веществах атомы и молекулы не имеют собственных магнитных моментов или они взаимно скомпенсированы, а намагниченность индуцируется внешним полем. (Пример: вещества с заполненными электронными оболочками типа инертных атомов.)
Согласно закону Ленца, индуцированный момент пропорционален и противоположен внешнему полю. Индуцированный момент существует, пока есть внешнее поле.
Диамагнитная восприимчивость определяется величиной индуцированного момента, т.е. числом электронов на орбите атома (растет с порядковым номером атома – это подтверждает эксперимент) и не зависит от температуры, так как определяется атомными эффектами.
Различают: 1) атомный (орбитальный) диамагнетизм и 2) электронный диамагнетизм (свободных электронов в плазме или в металле).
Диамагнетизм, определяемый орбитальным движением электронов, присущ всем твердым телам без исключения.
Большинство используемых сейчас полупроводников – диамагнетики.
Есть также диамагнитные металлы: Cu, Ag, Au, Zn, Ga и др.
Парамагнетики
Парамагнетизм связан с ориентацией элементарных магнитных моментов, и парамагнитная восприимчивость зависит от температуры (закон Кюри):
 (14.7)
(14.7)
Магнитные свойства электронных оболочек атома определяются строением их орбит, которое характеризуется квантовыми числами.
Квантовые числа: n – главное, L – орбитальное, S –суммарный спин, которые могут принимать значения:
n = 1, 2, ... ¥; L = 0, 1, ... n – 1;  и более
и более
 , (14.8)
, (14.8)
где  – обобщенное квантовое число.
– обобщенное квантовое число.
Магнитный момент атома:
 , (14.9)
, (14.9)
где mВ – магнетон Бора;
g – фактор спектроскопического расщепления или фактор Ланде:
 (14.10)
(14.10)
Парамагнетики:
1) атомы и молекулы (NO) с нечетным числом электронов;
2) атомы и ионы с незаполненными внутренними оболочками (Fe, Co, ... редкие земли);
3) некоторые молекулы с четным числом электронов (O2, S2, ...);
4) дефекты с нечетным числом электронов (F-центры, вакансии, дивакансии в Si);
5) большинство металлов.
Ферромагнетизм
Чистых ферромагнетиков всего 9: Fe, Co, Ni; а также 6 4f-металлов (Gd, Dy, Tb, Ho, Er, Tm), – зато много ферромагнитных сплавов, их намагниченность характеризуется петлей гитерезиса (рис. 14.2) с точками остаточной намагниченности JR и коэрцитивной силы Нс.
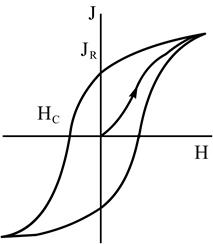
Рис. 14.2. Кривая гистерезиса перемагничивания ферромагнетика (JR – остаточная намагниченность, Нс – коэрцитивная сила)
Магнитная восприимчивость ферромагнетика (закон Кюри-Вейсса) зависит от Т:
 , (14.15)
, (14.15)
где q – температура Кюри – переход от ферромагнетика к парамагнетику (тепловое разрушение доменов).
Позже Френкель и Гейзенберг (1928 г.) установили, что причина поля Вейсса – обменное взаимодействие электронов. Это сильное электростатическое взаимодействие, при котором может быть выгодным состояние с параллельной ориентацией спинов. Обменное взаимодействие – чисто квантовомеханическое взаимодействие. Обменный интеграл при этом должен быть А > 0.
Для образования ферромагнетика необходимо выполнение условий:
1) атомы с недостроенными 3d- и 4f-оболочками;
2) обменный интеграл больше нуля;
3) большая плотность состояний в d- и f-зонах.
Области спонтанной намагниченности образуют ферромагнитные домены, ориентированные противоположно для минимизации полной энергии.
 (14.16)
(14.16)
Во внешнем поле домены ориентируются по полю до насыщения (ориентированы все в одном направлении). Ферромагнетики могут быть”мягкими” (JR и Нс малы) и “жесткими” (JR и Нс велики), что отражается на форме гистерезиса (рис. 14.3).

Рис. 14.3. Ферромагнетики: 1 - мягкий; 2 - жесткий
Магнитный резонанс
Магнитный резонанс – резонансное поглощение энергии переменного электромагнитного поля электронной или ядерной подсистемой вещества, находящегося в постоянном магнитном поле.
Ядерный магнитный резонанс (ЯМР)
ЯМР обусловлен квантовыми переходами в ядерной подсистеме вещества, находящегося в постоянном магнитном поле. Ядро с моментом I ¹ 0 во внешнем магнитном поле Но образует систему уровней (2 I + 1) с энергией (рис. 14.5):
 , (14.19)
, (14.19)
где g – гиромагнитное отношение ядра;
mI – магнитный момент ядра;
 – ядерный магнетон Бора;
– ядерный магнетон Бора;
g – фактор спектроскопического расщепления.
Поглощение электромагнитной энергии происходит при
 (14.20)
(14.20)
По правилам отбора Dm = ± 1.
В случае протона в поле mоНо = 1 Тл резонансная частота составляет 42,6 Мгц.
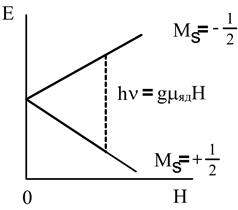
Рис. 14.5. Возникновение спектра ЯМР
Информация о твердом теле, получаемая с помощью ЯМР:
1. Водород в a-Si : H (количество и энергия связи).
2. Изотопный состав вещества, идентификация ядер.
3. Большие концентрации дефектов, влияющих на внутренние магнитные поля
4. Диффузионные процессы (исследуются по сужению линии с ростом Т).
5. Парамагнитные примеси в полупроводниках и диэлектриках.
6. Характер связей в твердом теле (по сдвигу резонансных частот).
Наиболее интересное практическое применение ЯМР – томография человека в медицине.
Электронный парамагнитный резонанс (ЭПР)
ЭПР обусловлен парамагнетизмом электронных оболочек и наблюдается в атомах, у которых нескомпенсированы спины (обычно нечетное число электронов).
Магнитный момент электронной оболочки  . Во внешнем поле Н энергетический уровень расщепляется на 2 J + 1 подуровня в соответствии с магнитным квантовым числом mj (рис. 14.6). Энергия:
. Во внешнем поле Н энергетический уровень расщепляется на 2 J + 1 подуровня в соответствии с магнитным квантовым числом mj (рис. 14.6). Энергия:
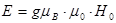 , (14.21)
, (14.21)
где g – фактор Ланде, g = 2 при L = 0, g = 1 при S = 0.



 , (14.22)
, (14.22)
где  – магнетон Бора (одинаков для всех электронов).
– магнетон Бора (одинаков для всех электронов).

Рис. 14.6. Наблюдение спектра ЭПР для 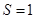
Так как mВ более чем в 1840 раз больше mяд, то и частоты резонанса соответственно выше: при mоН = 1 Тл и g @ 2, v ~ 30000 Мгц (~ 1 см), это диапазон СВЧ.
Метод ЭПР на 3 ¸ 4 порядка чувствительнее метода ЯМР из-за более высокой рабочей частоты.
В отличие от ЯМР, спектр ЭПР обычно состоит из большого числа линий, которое определяется эффективным спином парамагнитного центра в кристалле.
Информация, получаемая с помощью ЭПР:
1. Структура электронных оболочек атомов, характер их связей с решеткой (по числу линий ЭПР).
2. Концентрация примесных атомов и дефектов (по площади линии).
3. Вид окружения и его симметрия (в монокристаллах из угловой зависимости вида спектра).
4. Взаимодействие атомов с кристаллической решеткой (по релаксационным параметрам спектральной линии).
5. Оборванные связи в полупроводниках, в том числе в a-Si.
6. Свободные электроны и локализованные электроны.
Метод ЭПР широко применяется для исследований полупроводников и диэлектриков, тогда как ЯМР нашел применение в органической химии.
Резонансные методы позволяют исследовать механизмы физических явлений в твердых телах на атомном и ядерном уровне.
Физика конденсированного состояния
