Уравнение состояния идеальных газов. Газовая постоянная.

Основные параметры состояния (абсолютное давление, удельный объем и абсолютная температура) однородного тела зависят один от другого и взаимно связаны уравнением состояния F(P, v, T) = 0. Из молекулярно-кинетической теории следует, что абсолютное давление газа численно равно 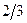средней кинетической энергии поступательного движения молекул, заключенных в единице объема:

(1.12)

где n - число молекул в удельном объеме; v - удельный объем газа; m - масса молекулы; v - средняя квадратичная скорость поступательного движения молекул; - средняя кинетическая энергия молекулы.

Молекулярно-кинетическая теория газов устанавливает прямо пропорциональную зависимость между средней кинетической энергией молекулы и абсолютной температурой:

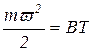(1.13)

где Т - абсолютная температура; В - коэффициент пропорциональности.

С учетом (1.13) уравнение (1.12) можно представить в виде

(1.14)

Если уравнение (1.14) отнести к двум состояниям газа, то для каждого из них получаем:

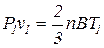
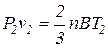
Почленное деление этих уравнений приводит к следующему соотношению:

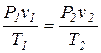(1.15)

Это соотношение между параметрами состояния может быть получено из совместного рассмотрения законов Бойля-Мариотта и Гей-Люссака, поэтому часто это соотношение называют объединенным законом Бойля-Мариотта и Гей-Люссака.

Выражение (1.15) показывает, что произведение абсолютного давления идеального газа и удельного объема, деленное на абсолютную температуру, для любого равновесного состояния есть величина постоянная:

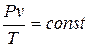. (1.16)

Постоянную величину обозначают R и называют удельной газовой постоянной:

или 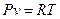(1.17)

Уравнение (1.17) называют термическим уравнением состояния идеальных газов или характеристическим уравнением, однозначно связывающим между собой параметры P, v, T. Это уравнение было выведено французским физиком Клапейроном в 1834 году и поэтому названо его именем.

Для произвольного количества газа массой m [кг] уравнение состояния имеет вид:

Pv = mRT, (1.18)

где P- абсолютное давление газа в Па; v - объем рассматриваемого количества газа в м³;

m - масса газа в кг; T - абсолютная температура газа в К.

Выясним физический смысл удельной газовой постоянной. Запишем уравнение Клапейрона для двух состояний газа при одном и том же давлении:

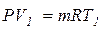
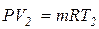
Вычитая из второго уравнения первое, получим:

P(V₂-V₁) = mR(T₂-T₁),(1.19)

откуда

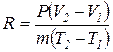. (1.20)

Числитель правой части представляет собой работу газа в процессе при постоянном давлении. Если разность температур равна 1К, а масса газа равна 1кг, то удельная газовая постоянная есть работа в Дж 1кг газа в процессе при постоянном давлении и при изменении температуры на 1К.

Удельная газовая постоянная имеет следующую размерность:

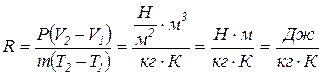
Удельная газовая постоянная представляет собой физическую постоянную, которая для каждого газа имеет вполне определенное значение, зависящее от природы газа и не зависящее от его состояния.

Уравнение Клапейрона в рассмотренном виде может применяться не только для идеальных газов, но и для реальных газов, имеющих низкое давление и высокую температуру.

Если m - молярная масса газа, то умножив на m обе части уравнения (1.17), получим уравнение Клапейрона-Менделеева:

Pvm = RmT; Pv_m = R_mT, (1.21)

где v_m = vm - молярный объем рабочего тела [м³/моль] при нормальных физических условиях (давлении 101325 Па и температуре 273,15К), объем 1 кмоль газа равен 22,4143 м³/кмоль;

R_m = mR - универсальная газовая постоянная, равная

Дж/(кмоль×К)

Уравнение (1.21) впервые было предложено Менделеевым в 1874 году и является наиболее общим для идеальных газов.

Газовая постоянная одного килограмма газа:

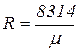. (1.22)

Смеси идеальных газов

Под газовой смесью понимается механическая смесь отдельных газов, не вступающих между собой ни в какие химические реакции. Каждый газ в смеси, независимо от других газов, полностью сохраняет все свои свойства и ведет себя так, как если бы он один занимал весь объем смеси. Молекулы каждого газа смеси создают давление на стенки сосуда, которое называется парциальным (частичным).

Газовая смесь идеальных газов подчиняется закону Дальтона: общее давление смеси газов равно сумме парциальных давлений отдельных газов, составляющих смесь:

Р = Р₁ +Р₂ + ... + Р_n = Р_i, (1.23)

где Р_i- парциальные давления.

Парциальным давлением называют такое давление, которое имел бы каждый газ, входящий в состав смеси, если бы этот газ находился один в том же количестве, в том же объеме и при той же температуре, что и в смеси.

Параметры газовой смеси могут быть вычислены по уравнению Клапейрона PV = mRT, где все величины, входящие в уравнение, относятся к смеси газов.

Задачей расчета газовой смеси является определение на основании заданного состава смеси средней молярной массы или газовой постоянной смеси газов, после чего получение всех остальных параметров можно произвести по уравнению состояния для смеси.

Газовая смесь может быть задана массовыми, объемными и мольными долями.

Массовой долей называют отношение массы каждого газа к общей массе смеси:

g₁ = m₁/m; g₂ = m₂/m; ...; g_n = m_n/m,(1.24)

где g₁, ..., g_n - массовые доли; m₁, ..., m_n - масса каждого газа;m- масса всей смеси.

Сумма всех массовых долей равна единице:

g₁ + g₂ + ... + g_n = g_i = 1 (1.25)

Сумма масс всех газов равна массе смеси:

m₁ + m₂ + ... + m_n = m_i = m.(1.26)

Объемной долей называют отношение парциального объема каждого газа к общему объему смеси газов:

r₁ = V₁/V; r₂ = V₂/V; ...; r_n = V_n/V, (1.27)

где r_1, ..., r_n - объемные доли; V₁, ..., V_n - парциальные объемы каждого газа;

V - объем смеси газов.

Парциальным объемом газа называют объем, который занимал бы этот газ, если бы его температура и давление равнялись температуре и давлению смеси газов. Парциальный объем каждого газа можно определить по закону Бойля-Мариотта. При постоянной температуре имеем:

V₁ = P₁V/P; V₂ = P₂V/P; ...; V_n = P_nV/P. (1.28)

Сложив правые и левые части этих выражений и учитывая закон Дальтона, получим:

V1 + V2 + ... + Vn = 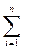Vi = V, (1.29)

т.е. сумма парциальных объемов газов, составляющих смесь, равна объему смеси газов.

Сумма объемных долей равна единице:

r₁ + r₂ + ... + r_n = r_i = 1 (1.30)

Задание смеси мольными долями равнозначно заданию ее объемными долями. Действительно, если мольной долей назвать отношение числа киломолей каждого газа (М_i) к числу киломолей смеси газов (М), то учитывая, что

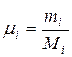и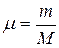

можно написать:

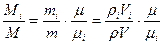(1.31)

Из закона Авогадро (r₁/r₂ = m₁/m₂ - плотности газов, находящихся при одинаковых температурах и давлениях, прямо пропорциональны их молярным массам) следует то, что при одинаковых Р и Т

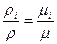. (1.32)

Тогда окончательно:

. (1.33)

Таблица 1.1 - Формулы для расчета газовых смесей

	Массовыми долями	Объемными долями
Перевод из одного состава в другой
Плотность и удельный объем смеси	;	;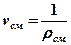
Кажущаяся молекулярная масса смеси
Газовая постоянная смеси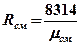
Парциальные давления компонентов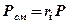

1.9 Теплоемкость газов

1.9.1 Основные определения. Массовая, объемная и мольная теплоемкости

Если к рабочему телу в каком-либо процессе подвести теплоту или отвести от него теплоту, то это приведет к изменению его температуры.

Отношение количества теплоты подведенной к рабочему телу (или отведенной от рабочего тела) в данном процессе к изменению его температуры называется теплоемкостью тела (системы тел):

[Дж/К], (1.34)

где dQ - элементарное количество теплоты; dT- элементарное изменение температуры.

Количество теплоты, подведенное к рабочему телу (или отведенное от рабочего тела) в каком-либо процессе х, для изменения его температуры на определенное количество градусов зависит от количества рабочего тела. В зависимости от количественной единицы рабочего тела, к которому подводится теплота, в термодинамике различают массовую (удельную), объемную и мольную теплоемкости

Удельная (массовая)теплоемкость с_х - это теплоемкость, отнесенная к единице массы рабочего тела:

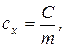[Дж/кг×К]. (1.35)

Объемнаятеплоемкость c'_х - это теплоемкость, отнесенная к единице объема рабочего тела при нормальных физических условиях (Р = 101325 Па и Т = 273,15 К):

[Дж/м³×К]. (1.36)

Мольнаятеплоемкость mc_x - это теплоемкость, отнесенная к количеству рабочего тела в молях:

[Дж/кмоль×К] (1.37)

где n - количество газа в молях.

Между указанными теплоемкостями существует следующая связь:

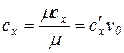, (1.38)

где v₀ - удельный объем при нормальных физических условиях;m- молярная масса.

Изменение температуры рабочего тела при одном и том же количестве сообщаемой теплоты зависит от процесса, в котором подводится теплота, поэтому теплоемкость является функцией процесса. Т.е. одно и то же рабочее тело в зависимости от процесса требует для своего нагрева на один градус различное количество теплоты. Численно величина с изменяется от до 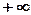.