Линейчатый спектр атома водорода
 Разреженные газы (отдельные атомы находятся на большом расстоянии друг от друга) испускают линейчатые спектры. Причем каждому газу присущ свой спектр, состоящий из отдельных спектральных линий гели групп близко расположенных линий. Водород – простейший атом, и его спектр наиболее изучен
Разреженные газы (отдельные атомы находятся на большом расстоянии друг от друга) испускают линейчатые спектры. Причем каждому газу присущ свой спектр, состоящий из отдельных спектральных линий гели групп близко расположенных линий. Водород – простейший атом, и его спектр наиболее изучен
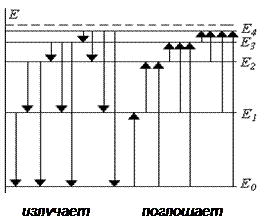
При переходе электрона с верхнего уровня на нижний (рис) атом излучает квант энергии 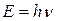
Чем больше разность энергий En-Em, тем больше частота излучения ( 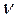 ) и тем меньше длина волны излучения
) и тем меньше длина волны излучения
( 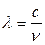 ).
).
Поглощая квант энергии hν, электрон переходит с
нижнего уровня на верхний .
Частота 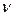 (или длина волны
(или длина волны 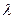 ), соответствующая той или иной линии спектра излучения определяется формулой Бальмера:
), соответствующая той или иной линии спектра излучения определяется формулой Бальмера:
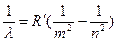 или
или 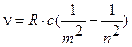
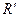 =1.10
=1.10  107 м-1 – постоянная Ридберга
107 м-1 – постоянная Ридберга
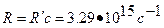 - тоже постоянная Ридберга
- тоже постоянная Ридберга
m – номер уровня на который переходит электрон;
n – номер уровня с которого переходит электрон.
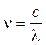 - частота
- частота
При переходе электронов с разных верхних уровней на какой-либо фиксированный уровень, спектральные линии образуют группу переходов, которая называется спектральной серией.
Например, если электроны переходят на первый ( m=1) уровень с более высоких уровней (n= 2, 3, 4, 5…), то все эти переходы объединяются в спектральную серию( серию Лаймана).
Каждая серия имеет название в зависимости от номера уровня, на который переходят электроны (рис.)
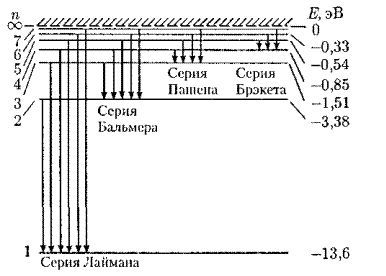
При:
m=1 – серия Лаймана;
m=2 – серия Бальмера (видимая часть спектра водорода);
m=3 – серия Пашена;
m=4 – серия Брэкета;
m=5 – серия Пфунда;
m=6 – серия Хэмфри.
Для серии Бальмера 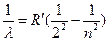 … или
… или 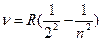
где (n=3, 4, 5…)
То есть, в видимой части спектра излучения в серии Бальмера присутствуют линии разного цвета (разной длины волны или частоты). На рисунке :
красная линия - это крайняя левая линия с самой маленькой ΔЕ (переход с 3-го уровня на 2-й )
фиолетовая линия – это крайняя правая линия в серии Бальмера, у которой самая большая ΔЕ.
Спектр поглощения возникает при переходе атома из стационарного состояния (n=1) в возбужденное при сообщении атомам извне определенной энергии, т.е. содержит только серию Лаймана.
Вывод: теория Бора блестяще справилась с описанием спектра излучения водорода и водородоподобных атомов, позволяет вычислять частоты спектральных линий. Однако теория Бора не может объяснить интенсивность линий и ответить на вопрос: почему совершаются те или иные переходы. Кроме того, попытки описать с её помощью уже следующий в периодической системе химических элементов атом гелия потерпели неудачу.
После открытия волновых свойств вещества стала очевидной необходимость построения новой более последовательной теории строения атома
Атом водорода в квантовой механике
Квантовые числа
В квантовой механике стационарное состояние электрона в атоме водорода определяется тремя квантовыми числами:
· n - главноеквантовое числоопределяет энергетические уровни электрона в атоме, от него зависит радиус орбиты и энергия электрона в атоме
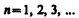
· l - орбитальное квантовое число определяет эксцентриситет орбиты или орбитальный момент импульса L электрона в атоме и может принимать значения
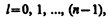
Различные значения l при данном n соответствуют движению электрона по эллипсу различной вытянутости. Совокупность всех электронов по этим эллипсам представляет собой электронный слой (оболочку).
слой K при п = 1
L при п = 2
M при п = 3
· mі магнитное квантовое число определяет проекцию вектора момента импульса электрона L на заданное направление, зависит от n и l. Может принимать значения
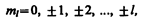
то есть имеет всего (2l+1) значений.
При помещении атома в магнитное поле наличие квантового числа mlприводит к расщеплению уровня с главным квантовым числом п на (2l+1) подуровней. Соответственно в спектре атома должно наблюдаться расщепление спектральных линий (эффект Зеемана).
Энергия
 Потенциальная энергия взаимодействия электрона с ядром, обладающим зарядом Ze (для атома водорода Z = 1),
Потенциальная энергия взаимодействия электрона с ядром, обладающим зарядом Ze (для атома водорода Z = 1),
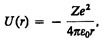 (1)
(1)
где r — расстояние между электроном и ядром.
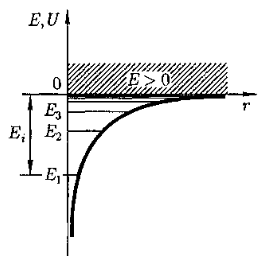
Графически функция U(r) изображена на рис. жирной кривой: U(r) с уменьшением r (при приближении электрона к ядру) неограниченно убывает.
Для учета волновых свойств электронов в квантовой механике используют уравнение Шрёдингера. С учетом (1) оно имеет вид:
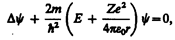 (2)
(2)
Уравнение (2) имеет решение только при определенных значениях энергии Е и волновой функции Y, которые задаются набором трех квантовых чисел n, l , m.
Другими словами, решение уравнения Шрёдингера содержит в себе три условия квантования, которые дают набор дискретный значений энергии и момента импульса электрона.
Полная энергия электрона в атоме (Е) определяется только главным квантовымчислом п:
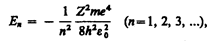 (3)
(3)
т. е. возможен только дискретный набор отрицательных значений энергии.
Возможные значения энергии электрона на разных уровнях ( Е1, E2, Е3,..) . показаны на рисунке в виде горизонтальных прямых. Самый нижний уровеньэнергии Е1, —основной, все остальные —возбужденные (Еn >Е1, n = 2, 3, ...).
При Е<0 движение электрона являетсясвязанным. Из рисунка следует, что по мере роста главного квантового числа n энергетические уровни располагаются теснее и при n=¥ E¥ = 0.
При Е>0 движение электрона являетсясвободным; область непрерывного спектра Е>0 (заштрихована на рис.) соответствуетионизованному атому. Энергия ионизации атома водорода равна
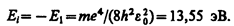 (4)
(4)
Выражение (3) и величина (4) совпадают с формулой, полученной Бором для энергии атома водорода.
3. Момент импульса
Наличие орбитальных квантовых чисел l и mі означает, что момент импульса (механический орбитальный момент) электрона квантуется, т. е. не может быть произвольным, а принимает дискретные значения, определяемые формулой
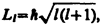
причем вектор Lмомента импульса электрона в атоме может иметь в пространстве 2l+1 ориентации, но лишь такие, при которых его проекция Llxна направление z внешнего магнитного поля принимает квантованные значения, кратные ћ:
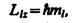
4. Состояния электрона в атоме
Хотя энергия электрона (3) и зависит только от главного квантового числа п, но каждому собственному значению Еn (кроме Е1) соответствует несколько собственных функций Y , отличающихся значениями l и ml.. Так , при данном п орбитальное квантовое число l может изменяться от 0 до (п–1) , а каждому значению l соответствует (2l+1) различных значений ml .
Следовательно, атом водорода может иметь одно и то же значение энергии, находясь в нескольких различных состояниях
Состояния с одинаковой энергией называются вырожденными. Общее число различных состояний с одинаковой энергией называется кратностью вырождения соответствующего энергетического уровня.
Кратность вырождения уровней водорода легко вычислить по формуле
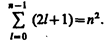
Состояния электрона с различными значениями орбитального квантового числа l принято условно обозначать следующим образом: l = 0 → s- состояние;
l = 1 → p- состояние;
l = 2 → d- состояние;;
l = 3 → f- состояние;;
Условное обозначение состояния электрона начинается со значения главного квантового числа п, далее буква, соответствующая значению l .
1 s,
2 s, 2 p,
3 s, 3 p, 3 d,
4 s, 4 p, 4 d, 4 f,
Согласно квантовой механике, каждому энергетическому состоянию соответствует волновая функция Y , квадрат модуля которой определяет вероятность обнаружения электрона в единице объема.
Вероятность обнаружения электрона в различных частях атома различна. Электрон при своем движении как бы «размазан» по всему объему, образуя электронное облако. Поэтому понятие боровской орбиты радиуса r представляется как состояние электронного облака, имеющего максимальную плотность (густоту) на этих расстояниях r.
Квантовые числа п и l характеризуют размер и форму электронного облака, а квантовое число ml характеризует ориентацию электронного облака в пространстве.
5.Спектр
Схему расположения уровней в атоме водорода можно представить, как показано на рис.
В квантовой механике правило отбора для орбитального квантового числа разрешает переходы только на соседние уровни
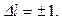
На рис. показаны переходы, разрешённые этим правилом. При каждом переходе излучается или поглощается квант энергии hν. Используя условные обозначения состояний электронов, переходы для серии Лаймана можно представить в виде:
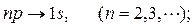
Для серии Бальмера -
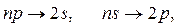
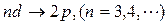
Рентгеновское излучение
Большую роль в выяснении строения атома, а именно распределения электронов по оболочкам, сыграло рентгеновскоеизлучение.
Возникает при соударении электронов, ускоренных высоким напряжением, с металлической мишенью из тяжелых Ме (Pt) внутри рентгеновской трубки.
Рентгеновское излучение – это электромагнитные волны с длиной волны 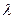 от 10-12 до 10-8 м.
от 10-12 до 10-8 м.
Спектр содержит 2 компоненты: сплошной спектр (зависит от энергии бомбардирующих электронов) и линейчатый спектр (отдельные max, характеризующие материал анода).
Сплошной спектр, ограничен границей сплошного спектра lmin,со стороны коротких длин волн. Линейчатый спектр это совокупность отдельных линий, появляющихся на фоне сплошного спектра.
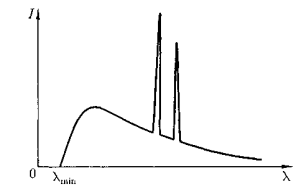 Сплошной спектр называется тормозным(т.к. он появляется в результате торможения быстрого электрона при взаимодействии с атомами мишени).
Сплошной спектр называется тормозным(т.к. он появляется в результате торможения быстрого электрона при взаимодействии с атомами мишени).
Линейчатый спектр называется характеристическим.
Частота характеристического спектра определяется законом Мозли
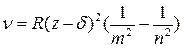
Где: 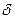 - const экранирования;
- const экранирования;
z – порядковый номер элемента в таблице Менделеева.
Закон Мозли позволяет по измеренной длине волны рентгеновских линий точно устанавливать атомный номер данного элемента.
