Понятие о меркаторской проекции

На морскую навигационную карту, т. е. карту, предназначен­ную для судовождения, требуется наносить линии истинных пе­ленгов и курсов, снимать и откладывать на них расстояния. Поэтому эти карты долж­ны удовлетворять следующим требовани­ям:

линия постоянного курса — локсодро­мия — должна изображаться простейшим образом, т. е. в виде прямой;

направления на карте относительно ис­тинного меридиана между какими-либо точками должны быть равны направлени­ям между теми же точками на местности (проекция карты должна быть равноуголь­ной).

Этим требованиям полностью удовлет­воряет карта, построенная в проекции следующего вида. Представим, что земной шар (взятый в уменьшенном виде) окру­жен цилиндром, касающимся экватора (рис. 56). В этом случае земная ось совпа­дает с осью цилиндра. Спроектируем из центра земного шара меридианы и парал­лели на боковую поверхность цилиндра, т. е. проведем через все их точки лучи из центра Земли к этой поверхности. Таким образом на рис. 56 точки а, Ь, с, d явля­ются проектируемыми. При этом получим в виде прямых линий и параллели в виде окружностей, увеличенных до размеров эк­ватора.

Если развернуть боковую поверхность цилиндра на плоскость, то на ней образуется прямоугольная картографическая сетка. При этом все меридианы окажутся параллельными друг другу. Следо­вательно, локсодромия как линия, пересекающая все меридианы под одним и тем же углом, изобразится прямой. Таким образом,

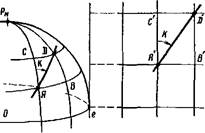Рис. 57. Участок земной поверхности на меркаторской карге.

первое требование, предъявляемое к навигационной карте, будет выполнено.

На построенной нами картографической сетке расстояния меж­ду меридианами во всех широтах получились одни и те же, т. е. каждая параллель как бы растянулась до размеров экватора. Поэ­тому какой-либо участок на земной поверхности, вписанный меж­ду меридианами и параллелями и имеющий трапецеидальную фор­му, например участок А, В, С, D (рис. 57), изобразится на полу­ченной сетке в виде прямоугольной фигуры А', В', С', D'.

В нашем построении каждая параллель с радиусом г в данной широте, имеющая, следовательно, длину 2кг, увеличилась на карте до размеров экватора, длина которого при радиусе R равна

9тс/?

2kR, т. е. параллель увеличилась по длине в-------------------- раз, или во

2кг

столько же раз, во сколько радиус экватора больше радиуса па­раллели в данной широте.

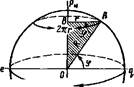
Из прямоугольного треугольника АОВ (рис. 58), образованно­го радиусом R экватора (гипотенуза), радиусом г параллели в данной широте (катет) и отрезком земной оси ОВ (другой катет) при угле ф, обозначающем широту места, следует

2 tR R —— = — == sec tp,2 кг г ^т

т. е. каждая параллель на карте в данной проекции увеличивает­ся по длине пропорционально секансу широты данной параллели.

2srR

Рис. 58. Зависимость длины параллели от ши­роты.

Чтобы сохранить подобие фигур на земной поверхности и изо­бражение их на карте, а вместе с тем и равенство направлений,
необходимо, чтобы и меридианы на карте оказались растянутыми в той же степени, что и параллели в данной широте.

Это значит, что каждый элемент меридиана между соседними, бесконечно близкими друг к другу параллелями должен быть рас­тянут также пропорционально секансу широты, которую между этими бесконечно близкими друг к другу параллелями можно счи­тать неизменной, т. е. эти фигуры, полученные на карте, будут подобны соответствующим фигурам на местности.

Подобные же фигуры обладают равенством углов между соот­ветствующими сторонами. Линия курса, проходящая, например, между точками А и D на местности под углом К к меридиану (см. рис. 57), пройдет между соответствующими точками А' и D' на карте под тем же углом К■ Таким образом, выполнится и второе требование, предъявляемое к навигационной карте, — равноуголь- ность.

Рассмотренная проекция называется цилиндрической нормаль­ной проекцией Меркатора.