Интеграл Фурье для чётной и нечётной функции
Интеграл Фурье для чётной и нечётной функции
Основные сведения
Функция f (x ), определенная на всей числовой оси называется периодической , если существует такое число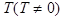 
, что при любом значении х выполняется равенство 
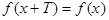. Число Т называется периодом функции.
Отметим некоторые свойства этой функции:
1) Сумма, разность, произведение и частное периодических функций периода Т есть периодическая функция периода Т .
2) Если функция f (x ) период Т , то функция f (ax )имеет период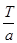 
.
3) Если f (x )- периодическая функция периода Т , то равны любые два интеграла от этой функции, взятые по промежуткам длины Т (при этом интеграл существует), т. е. при любых a и b справедливо равенство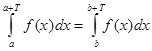 
.
Тригонометрический ряд. Ряд Фурье
Если f (x ) разлагается на отрезке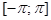 
в равномерно сходящийся тригонометрический ряд:
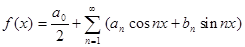(1)
то это разложение единственное и коэффициенты определяются по формулам:
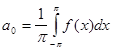
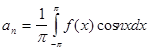
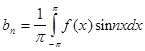, где n =1,2, . . .
Тригонометрический ряд (1) рассмотренного вида с коэффициентами называется тригонометрическим рядом Фурье , а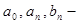 
коэффициентами ряда Фурье.
Достаточные признаки разложимости функции в ряд Фурье
Точка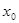 
разрыва функции 
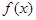называют точкой разрыва первого рода, если существует конечные пределы справа и слева этой функции в данной точке.
ТЕОРЕМА 1 (Дирихле). Если 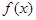периодическая с периодом 
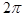функция непрерывна или имеет конечное число точек разрыва 1-ого рода на отрезке [ 
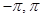] и этот отрезок можно разбить на конечное число частей, в каждом из которых f (x ) монотонна, то ряд Фурье относительно функции сходится к f (x ) в точках непрерывности и к среднеарифметическому односторонних пределов в точках разрыва рода (Функция удовлетворяющая этим условиям называется кусочно-монотонной).
ТЕОРЕМА 2. Если f (x ) периодическая функция с периодом 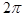, которая на отрезке [ 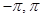] вместе со своей производной непрерывна или имеет конечное число точек разрыва первого рода, то ряд Фурье функции f (x ) в точках разрыва к среднему арифметическому односторонних пределов (Функция удовлетворяющая этой теореме называется кусочно-гладкой).
Интеграл Фурье для четной и нечетной функции
Пусть f (x )-четная функция, удовлетворяющая условиям представимости интегралом Фурье.
Учитывая, что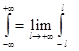 
, а также свойство интегралов по симметричному относительно точки x =0 интервалу от четных функций, из равенства (2) получаем:
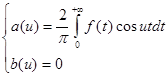(3)
Таким образом, интеграл Фурье четной функции f (x ) запишется так:
,
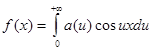где a (u ) определяется равенством (3).
Рассуждая аналогично, получим, для нечетной функции f (x ) :
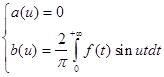(4)
и, следовательно, интеграл Фурье нечетной функции имеет вид:
,
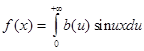где b (u ) определяется равенством (4).
Рис. 1
Производная также непрерывна везде, кроме конечного числа точек разрыва первого рода. Вывод: функция удовлетворяет условию разложения в ряд Фурье.
1) F(x) - кусочно-непрерывна на интервале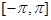 
.
2) F(x) - кусочно-монотонна.
Так как отсутствует симметрия относительно OY, а также центральная симметрия - то рассматриваемая функция произвольна.
Интеграл Фурье для чётной и нечётной функции
Основные сведения
Функция f (x ), определенная на всей числовой оси называется периодической , если существует такое число 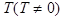, что при любом значении х выполняется равенство 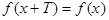. Число Т называется периодом функции.
Отметим некоторые свойства этой функции:
1) Сумма, разность, произведение и частное периодических функций периода Т есть периодическая функция периода Т .
2) Если функция f (x ) период Т , то функция f (ax )имеет период .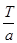
3) Если f (x )- периодическая функция периода Т , то равны любые два интеграла от этой функции, взятые по промежуткам длины Т (при этом интеграл существует), т. е. при любых a и b справедливо равенство 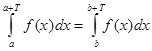.