Общие соображения, распространение сил

В предлагаемой вниманию читателя ЧАСТИ ВТОРОЙ я намерен исследовать формулы элементарных воздействий, к которым, как мы видели, была сведена в предыдущем анализе математическая теория Лоренца, а также показать, что мы можем устранить абсолютное движение, причём без заметного расхождения с экспериментом. Я буду использовать ныне существующие физические гипотезы: о природе электричества, токе проводимости, диэлектриках, и т.д., и особенно принцип суперпозиции, говорящий о полной независимости воздействий со стороны разных зарядов, входящих в систему.1

Для этого я буду вынужден предложить новую модель распространения электродинамических воздействий. Но, как было сказано во ВВЕДЕНИИ, я не стану обрисовывать все её следствия, а ограничусь пока только работой критика.

Первое следствие вытекает непосредственно из принципа относительности. В теории эфира материальная точка P, покоящаяся относительно окружения, способна испускать волны с постоянной радиальной скоростью, образуя в каждый момент времени систему сфер с центром в т. P. Если же P придёт в движение, то сферы станут уже эксцентричными, и каждая сохранит центр в той точке P₁ эфира, которая совпадала с P в момент испускания волны. Напротив, согласно принципу относительности, если движение равномерное, сферы должны оставаться концентричными, как в покое, с центром в т. P. Если движение перестанет быть равномерным, то принцип будет уже не достаточен для определения движения волн.

В оптике успешно применялись два разных способа представления явлений: посредством излучения [по Ритцу эмиссии – С.С.] (свет движется) и посредством эфира (свет распространяется в среде).2 Второй вводит абсолютное движение, тогда как первый приводит к движению света в вакууме именно так, как того требует принцип относительности: световые частицы в момент t разлетаются по всем направлениям, двигаясь с постоянной радиальной скоростью и формируя сферу с центром, движущимся со скоростью v, которую имела т. P в момент испускания. Если v постоянна, то этот центр продолжает совпадать с P.

Лишь этот фундаментальный принцип мы и заимствуем у эмиссионной теории [ньютоновской теории истечения света – С.С.]. Можно добавить, что эти частицы следует рассматривать исключительно как вспомогательное искусственное представление, достаточно удобное, и позволяющее, как мы видели, принять для скорости света в вакууме точный закон, даже если скорость P переменна и принцип относительности не применим. Тогда скорость света зависит от скорости, имевшейся у его источника в момент испускания. С этого момента скорость частиц остаётся неизменной и не зависящей от последующего движения P, даже если частицы проходят через весомые тела или электрические заряды. Я указал во ВВЕДЕНИИ, что эта гипотеза, требуемая принципом суперпозиции, является только временной и противоречит принципу действия и противодействия, но преимущество её в том, что она насколько это возможно близка к соответствующим гипотезам Лоренца, и это делает её предпочтительной для цели, которую я здесь ставлю.

Кроме того, мы будем считать, что воздействие точки P на тело P ' будет зависеть только от скоростей, расположения и других [кинематических] характеристик частиц, испущенных P и достигших P ' в рассматриваемый момент.

Мы могли бы попробовать объяснить явления механическими воздействиями, оказываемыми этими частицами, но трудности, к которым мы придём при этом, кажутся непреодолимыми. Вместо того чтоб искать способ сохранения схемы классической механики с "невидимыми массами" или "связями", и с тому подобным, я предпочел по максимуму уменьшать число гипотез - метод, имеющий с точки зрения логики и ясности преимущество, возмещающее недостатки "механических аналогий" Максвелла. Мы увидим, между прочим, что механическая масса может быть выведена, как и в теории Лоренца, из чисто электрических воздействий, и что помимо этого, теория применима к тяготению и, возможно, к молекулярному движению. Это позволило бы охватить классическую механику и представить кинетические и потенциальные явления как имеющие один и тот же источник происхождения. При этом в фундаментальных гипотезах логичней руководствоваться лишь кинетическими соображениями, пользуясь единственно понятиями времени, пространства и электрического заряда.

Поэтому я буду допускать, что любая заряженная точка испускает в каждый момент времени по всем направлениям фиктивные частицы, бесконечно малые и запущенные при рождении с одинаковой радиальной скоростью c, которые сохраняют своё равномерное движение, независимо от того, какие им встречаются тела 3. Ансамбль частиц, испущенных в момент t ' движущейся точкой P ' (с координатами x ', y ', z ', являющимися функциями аргумента t ') формирует в каждый последующий момент t сферу радиуса

Центр сферы, которая продолжает двигаться со скоростью v ' = v ' (t ') точки P ', в момент t ' имеет координаты

.

Поэтому уравнение сферы будет

Если x ', y ', z ' - известные функции времени t ', то можно исключить из этих двух уравнений момент t ' излучения волны, которая достигает заданной точки P с координатами x, y, z, находящейся в момент t, как это следует из сказанного, на расстоянии равном радиусу r сферы, образованной в этот момент и заданной уравнением

В теории Лоренца, при выборе системы координат фиксированной относительно эфира, мы, напротив, имели бы следующие уравнения:

Новая гипотеза даёт полное равноправие двух точек P и P ', движущихся равномерно: r в этом случае будет действительным расстоянием между точками в момент t. Две волны, испущенные одновременно в P ' и P, придут соответственно в P и P ' тоже одновременно. В теории Лоренца это иначе. В итоге, если наша теория в случае измеримого равномерного движения (где излучение, следовательно, отсутствует) будет вести к равенству действия и противодействия, то в теории Лоренца этого не будет. И лишь если моменты излучения не будут совпадать, этот принцип должен быть изменён а также расширен.

Рассмотрим снова случай, когда P ' участвует в колебательном движении, а расстояние PP' является достаточно большим. Это позволит волнам, стартовавшим в моменты , когда скорость P ' имела разные значения , приходить в P одновременно, вследствие разницы скоростей их распространения (практически этот случай будет представлен только в оптике). В теории же Лоренца, чтобы подобное явление имело место, точка P ' должна была бы приобретать в некоторые моменты времени скорость превосходящую скорость света.

Если – это ускорения точек (x,y,z), (x',y,'z'), и если, кроме того,

– это компоненты относительной скорости точки P (x, y, z) и центра C сферы, испущенной P ' и достигающей P в момент t. Если P ' движется равномерно, то это будет просто относительная скорость P и P'.

Вектор r, компоненты которого

представляет собой, как мы видели, линию, соединяющую P ' и P, где P ' сохраняет скорость постоянной по величине и направлению, начиная с момента излучения

этот вектор направлен от P ' к P. И мы имеем

Относительная скорость U частиц, испущенных P ', имеет относительно P составляющие

её квадрат – это

проектирование её на rдаёт

Относительное положение и движение сферы и точки P фактически задаются величинами r, u_r и u² или, что то же самое, r, U_r и U². Не существует такой комбинации векторов r, u, независимой от их абсолютного положения в пространстве, которая не могла бы быть выражена тремя этими величинами.

Мы можем также заметить, что для наблюдателя, помещённого в точку P и участвующего в её движении, отношение расстояния вдоль нормали между двумя последовательными положениями сферы к промежутку времени dt, соответствующее скорости распространения волны для этого наблюдателя, в точности равно U_r.

Наконец, если мы примем, что число частиц, испускаемых заряженным центром в течение периода dt ' пропорционально его заряду e ' и dt ', то число частиц, расположенных в элементе поверхности dS сферы, не будет зависеть от положения этого элемента и будет пропорционально . Если две сферы, испущенные в моменты t ' и t '+dt', отстоят вдоль нормали в точке (x,y,z) в момент t на расстояние dn, то мы получим

Тогда количество частиц в элементе объёма dSdn пропорционально , и плотность D будет , где ca – универсальный множитель пропорциональности. Если r=c (t-t '), мы тогда окончательно получим

Уравнение (II) задаёт r как неявную функцию переменных x, y, z, t, если задано движение точки P '. Дифференцируя его, мы имеем

откуда

так что это приводит к

и, аналогично, к членам ближайшего превосходящего порядка,

Производные от r и D по x, y, z дадут тогда ускорения.

Рассматривая x, y, z как функции от t, формулу следует записать

(6) *

ЭЛЕМЕНТАРНАЯ СИЛА

Мы видели, что теория Лоренца в последнем анализе выражена утверждением элементарного закона взаимодействия между двумя заряженными элементами объёма. Движущаяся частица P ' (x ', y ', z '), несущая заряд e ', воздействует на другую P c зарядом e, расположенную в т. (x,y,z), c силой, зависящей от скорости v этой последней, от направления , ... и от радиуса R волны, испущенной P ' в момент t ' = t - R/c и достигающей P в момент t, и, наконец, от скорости v ' и ускорения w ' точки P ' в момент t '. Мы имеем (в системе координат, покоящейся относительно эфира)

,

уравнение, задающее R как неявную функцию от x, y, z, t, если заданы функции x '=x' (t '), y ', z '. Тогда мы получаем

уравнения, аналогичные (4) и (5).

Элементарная сила, выражения для которой были даны Шварцшильдом1 для двух электронов с диаметром много меньшим расстояния между ними, имеет одну составляющую параллельную R, другую параллельную v ', и третью параллельную w '. Мы имеем

Уравнения движений будут

где суммирование ведётся по всем электронам. И далее по принципу Даламбера получим

Мы намерены, сохраняя пока уравнения (V^a) и (V), преобразовать выражение для F в такой вид, который исключал бы абсолютное движение. Последнее явно входит в выражение через абсолютные скорости v, v ', и менее явно - через закон распространения.

В ОБЩИХ СООБРАЖЕНИЯХ мы уже показали, что принцип невозможности действия на расстоянии будет выражен условием, по которому F зависит только от расположения и от скорости частиц вокруг e, другими словами, от векторов U, r и D, а также от первых производных r, D по x, y, z. Эти производные дают, как мы уже сказали, ускорение w '. Также естественно рассматривать F как величину пропорциональную плотности D частиц возле зарядов e и e. Тогда мы можем, совсем как в формуле Лоренца, разложить вектор F вдоль направлений r, U, w ' и записать

Величины A₁, B₁, C₁, не зависящие от системы координат, в соответствии с гипотезой зависят только от r, U², U_r. Если U_x=c cosrx-ux и U², U_r выражены линейно через u², u_r, мы можем также записать

где A₂, B₂, C₂ - функции от u², u_r. И мы будем считать, что они не зависят от r. Кроме того, для этих выражений, содержащих скорости c, u в однородном виде, мы можем записать для скоростей, являющихся малыми в сравнении со скоростью света, (используя n, m, p – специально подобранные показатели степени)

Хотя эта гипотеза и не обязательна, мы предположим, что, если изменить знак скоростей, то A₂, B₂, C₂ не будут меняться. Другими словами, они, даже будучи функциями , после раскрытия не будут содержать нечётных степеней .

Заменяя D его значением из (5), и расставляя часть коэффициентов мы, наконец, сможем записать F_x в форме

где k, a_i, b_i, c_i - коэффициенты, остающиеся независимыми в имеющихся условиях опыта, который подразумевает также, что φ, ψ, χ - это неизвестные пока функции.

Члены с порядком выше второго играют роль только в давлении света (что относится к оптике, и, следовательно, нас не затрагивает) и при изучении лучей радия. Поэтому не удивительно, что они точно не определены. Всё же мы увидим, что даже члены второго порядка, от которых электродинамические явления уже зависят, полностью не определены экспериментом: величина k остаётся произвольной. Поэтому предложенная формула оказывается весьма общей для цели, которую мы преследуем. Впрочем, это ещё не самая общая формула, и рассмотрение вращательных [орбитальных?] движений электронов по многим причинам было бы недостаточно исчерпывающим.

Уравнения движения по-прежнему будут (V) и (V^a). В рассмотренном выше случае, когда волны, испущенные в разные моменты одним и тем же электроном e ' одновременно достигали электрона e, приняв во внимание каждое из этих воздействий, мы будем иметь суммы .

Чтобы показать, что новая теория успешно включает в себя все факты, известные в области классической электродинамики, я для начала рассмотрю случай, когда скорости и ускорения сравнительно невелики. В частности это верно для всех явлений из области классической электродинамики, катодных лучей, и проч. Это объясняется тем фактом, что мы можем разложить все играющие роль функции вида в быстро сходящиеся ряды, взятым по степеням , и оставив только первые их члены. Я называю это случаем медленных вариаций.

Вторым я рассмотрю случай произвольного ускорения и ничтожно малых в сравнении с c скоростей: так обстоит дело в генераторе Герца и во многом в оптике.

Наконец, когда скорости сопоставимы c c, но ускорения остаются невелики, мы приходим к эксперименту Кауфмана с β-лучами радия.

Все электрические явления, наблюдавшиеся до сих пор, относятся к одной из этих категорий.

Мы знаем, что закон сохранения энергии в его классической форме W=const не применим, если имеется излучение. И потому мы должны обратиться к модели потока энергии, рассматривая энергию колебаний, потерянную светящимся телом или генератором Герца, как излучаемую в пространство со скоростью света и соответствующим импульсом, согласно теореме Пуанкаре. От неё до идей, которые мы только что выразили, остаётся только один шаг. Но, зайдя в эту область, я бы слишком отклонился от критической цели, которую я здесь непосредственно ставил. И потому я ограничусь тем, что покажу – во всех явлениях, наблюдавшихся до сих пор, силы, движения и, следовательно, работа будут совершенно теми же, что и в теории Максвелла. А закон энергии, в той мере, в какой он был проверен в данной области, оказывается следствием этого.

Вместе с законом энергии, принцип Мопертюи наименьшего действия, который подразумевает уравнение энергии в его классической форме, в общем случае тоже перестаёт быть справедливым, подобно каноническим уравнениям и уравнению Гамильтона-Якоби в частных производных. Ничто не даёт нам повода считать принцип Гамильтона исключением из общего правила. Чтобы сделать его применимым к формуле (VI), необходимо было бы ввести в него член, содержащий ускорение заряда e, другими словами, инерционное противодействие, зависящее от расположения внешних зарядов. Формула Вебера содержала член такого вида, и Гельмгольц2 показал недопустимые следствия этого. Для изолированного электрона, для которого приближённое значение отношения , движущегося внутри пустой заряженной сферы, всё выглядело бы так, словно масса уменьшается пропорционально потенциалу сферы и становится нулевой при его примерном значении в вольт (плюс). Ускорение в таком случае стало бы бесконечным, и мы можем видеть, что такой эксперимент было бы не так сложно поставить. В оптике и для спектральных колебаний, где инерционная отдача играет важную роль, влияние электрических зарядов аппаратуры на оптические свойства и положение лучей в спектре, следующее из введения такого члена, совершенно противоречило бы эксперименту. И лишь если б функция Лагранжа, как в теории Лоренца3, линейно зависела от скорости v заряда e,можно б было избежать этих следствий. Однако это потребовало бы введения абсолютного движения. При этом принцип Гамильтона, рассматривающий лишь относительные скорости, нуждался бы в соответствующем преобразовании.

Уравнения движения, которые мы только что записали, имеют второй порядок, подобно уравнениям механики, но из-за аргумента они в то же время являются функциональными уравнениями, и это очень сложная, смешанная форма не может быть определена.

СЛУЧАЙ МЕДЛЕННЫХ ВАРИАЦИЙ

§3. - ОБЩЕЕ ВЫЧИСЛЕНИЕ СИЛ*

Преобразуем выражение для F, исходя из гипотезы, по которой решения

быстро сходятся, и приближённо вычислим F вплоть до членов третьего порядка (до c^-3).

Обозначим через ρ вектор с компонентами – x (t)-x '(t), y (t)-y '(t), z (t)-z '(t), другими словами, имеющееся на данный момент расстояние между двумя заряженными точками. И пусть A_ρ - компонент вектора A в направлении ρ. Тогда мы будем иметь, согласно (2),

откуда, наконец, имеем

(11)

Аналогично

(12)

Выражения для u², u_r² входят в выражение для F только с множителем 1/c², их рост останавливается на первом члене: u² будет квадратом текущей относительной скорости двух точек, находимым как

и

Если пренебречь членами, которые в выражении (VI) для F умножались бы на 1/c³, то это выражение, наконец, перейдёт в

(13)

где, снова напомним, все величины должны быть взяты для момента t. Итак, мы снова нашли наиболее удобную форму воздействия на расстоянии. Можно заметить, что действие не равно противодействию, но вся разница кроется только в члене, содержащем ускорения, а не скорости.

Эта формула может быть также записана в виде

Теперь

и .

Выражение в первых круглых скобках будет, с учётом

как в известном законе Вебера. Выражение во вторых скобках представлено законом Римана1. Третьи скобки равны

В целом, мы теперь имеем для скоростей наиболее общую линейную комбинацию из двух законов, предложенных Вебером и Риманом для объяснения электрических явлений. Уже известно - это легко доказать, - что эти две формулы могут быть записаны в классическом виде

,

где для закона Вебера, и для закона Римана.

Их линейная комбинация будет предположительно иметь тот же вид, и, положив

(14)

мы будем иметь

(15)

Сформулировав весьма специфические гипотезы относительно природы тока проводимости, которые сегодня должны рассматриваться как неприемлемые, по крайней мере для электролитов, Вебер и Риман показали, что их формулы представляют собой известные законы электродинамики и индукции в замкнутых цепях. Мы покажем, что этот результат не зависит от этих частных гипотез2, и что он может быть распространён даже на воздействия замкнутых токов свободных ионов, скажем, катодных лучей, и на действия, оказываемые при движении статическим электричеством на магнит (другими словами, систему замкнутых токов). Во всех явлениях такого рода, наблюдавшихся прежде, имеется, по крайней мере, одна замкнутая цепь, и это очень важная особенность. Что же касается явлений индукции в открытых цепях, то если коротко, они зависят лишь от члена, содержащего ускорение w '. Однако мы увидим, что этот член одинаков в обеих теориях: это полностью подтверждается экспериментами с генераторами Герца. И можно утверждать, что все экспериментальные выводы Максвелла и теории Лоренца основаны только на этом члене и на факте распространения. А что касается формы, в которой эти скорости входят в формулу элементарной силы, то мы не более осведомлены в этом вопросе, чем были Вебер, Риман и Клазиус, несмотря на эксперименты с лучами катода, эффект Роуланда и другие.

Интересно сравнить эту формулой с той, которая следует из теории Лоренца, если мы разложим их в ряд вплоть до членов 2-го порядка. Это приводит, согласно (III) к выражениям

где величины v ', w ' берутся в момент времени t. Мы решаем это уравнение относительно R и снова раскладываем в ряд, и тогда оно преобразуется в

То же и в отношении членов порядка 1/c² [поскольку скорость входит в (IV) с множителем 1/c, то это будет достаточно точным приближением],

Выражение для потенциалов Ф, A, данное Ленардом и Вихертом3, будет

Составляющая силы, для которой общее выражение потенциалов будет

принимает, после приведения к членам порядка 1/c², вид

Мы видим, что это выражение сходно с (13) только тем, что содержит электростатический множитель 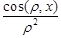и ускорения. Мы можем выразить это в виде

если, как указано Шварцшильдом, принять

это даст

§4. - ЭЛЕКТРОСТАТИКА*

Если электрические заряды находятся в покое или входят в состав одного и того же тела, будучи вовлечены в общее равномерное движение, формулы (13) и (20) преобразуются в

Это есть не что иное как закон Кулона. Очевидно также, что в нашей теории количества электричества измеряются в электростатических единицах, подобно тому, как это имеет место в теории Лоренца.

Вместе с Лоренцем мы рассматриваем весомые диэлектрики как образование из положительно и отрицательно заряженных атомов, причём полный заряд каждого элемента объёма равен нулю. На эти атомы действуют упругие силы, стремящиеся вернуть их в положение равновесия, если они изолированы от действия внешних сил. Поляризация диэлектриков и связанные с ней эффекты в обеих теориях объясняется одинаково, что в итоге приводит к одинаковым соотношениям.

ЭЛЕКТРИЧЕСКИЕ ТОКИ

Электронная теория рассматривает токи проводимости в металлах, а также токи в электролитах и газах, как движение электрических зарядов: положительные ионы движутся в направлении противоположном движению отрицательных ионов. Рассмотрим элемент объёма dτ тела, в котором протекает ток и который содержит множество ионов. Пусть V - их скорость, Ni, ei- соответственно число единиц объёма и заряда одного вида ионов, образующих поток. Скорость иона относительно тела будет v-V. Эта величина характеризует ток, интенсивность которого, измеренная в электростатических единицах, есть, в соответствии с гипотезой1

Электростатический заряд Edτ элемента

и вектор

представляет собой конвективный ток [названный так, видимо, по аналогии с конвективным переносом тепла – С.С.], проявления которого изучал Роуланд и другие.

Соседние ионы оказывают сложное воздействие на движущиеся, и мы допускаем, что в среднем это отражается на сопротивлениях –KJx, -KJy, -KJz, пропорциональных относительным скоростям (K – постоянная). На величину Jслучайные движения молекул не окажут заметного влияния. Ионы не могут покидать поверхность проводника, за исключением случая контакта с другим проводником.

Как было установлено, формулы (13) и (20) содержат кроме электростатического члена, только члены, поделённые на огромную величину c²=9·10²⁰ см²/с². Эти члены окажутся заметными, лишь если скорости или ускорения будут чрезвычайно велики, или если заряды, задействованные в игре, будут несоизмеримо больше тех, что мы имеем в электростатике. Изучение электролитов и эффекта Холла показало, что скорости ионов и электронов таковы, что v/c является крайне малым, порядка 10-10. Этот результат заметно упрощает теорию. Электрический заряд Edτ элемента объёма найдётся как разница двух несопоставимо бóльших зарядов: положительного заряда E₁dτ и отрицательного –E₂dτ, оба порядка 10¹⁰Edτф. Мы будем называть такой ток нейтральным током.

Мы значительно упростим вычисления, не влияя заметно на результаты, если допустим, что имеются только два вида ионов, один положительный, другой отрицательный, и что только последний движется относительно вещества проводника, в то время как положительные заряды прикреплены к этому веществу и имеют, подобно ему, скорость V. Поэтому мы имеем

Читатель будет уведомлен, когда эта гипотеза скажется на результатах.

Мы знаем, что в рамках классических теорий различие между замкнутыми и не замкнутыми токами было необходимо. У нас это остаётся всё ещё так. Лишь первые могут оставаться постоянными (в установленных пределах). Что же касается вторых, то гипотезы, принятые относительно E₁и E₂, показывают, что начала и концы этих элементов с токами будут нести, спустя небольшое время, весьма большие свободные электрические заряды, которые заметно изменят условия движения (тока). Вообще, в связи с этим открытые токи изменяются слишком быстро, за исключением разве что случая, если мы сможем при помощи сверхчувствительных приборов регистрировать движение крайне малых зарядов.

Мы будем считать, как того требует электронная теория, и в соответствии с воззрениями Ампера, что магниты - это системы замкнутых нейтральных токов.