Теплоемкость идеальных газов.

Теплоемкостью тела в каком-либо процессе изменения его состояния называется количество подведённой (или отведённой) теплоты, необходимое для повышения (или понижения) его температуры на один градус.

В термодинамике газов различают:

· массовую теплоемкость с, кДж/(кг·град),

· объемную теплоемкость с^/ , кДж/(м³×град),

· мольную теплоемкость 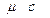, кДж/(кмоль×град).

,

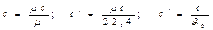где 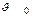– удельный объем при нормальных условиях.

Теплота является функцией процесса:

для элементарного термодинамического процесса 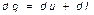. Как было сказано выше, внутренняя энергия обладает полным дифференциалом, а работа изменения объёма – нет. Значит, сумма 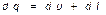не обладает свойствами полного дифференциала.

Поэтому понятие теплоемкости имеет смысл лишь в том случае, когда задан характер процесса, в котором газу сообщается теплота.

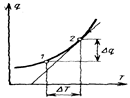
Связь между теплотой процесса и температурой газа

,

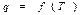Очевидно, что на различных участках такой кривой одному и тому же изменению температуры соответствуют различные количества подведенной теплоты, поэтому и значения теплоемкости на этих участках будут различными.

Вводят понятие о теплоемкости, средней в заданном интервале температур от Т₁ до Т₂ (т.е. на участке 1–2).

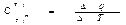
Значение истинной теплоемкости при заданной температуре:

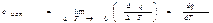
Истинная теплоемкость математически выражается как первая производная теплоты по температуре (при условии, что задан характер процесса).

В термодинамике особо важную роль играют теплоемкость при постоянном объеме

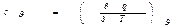
и теплоемкость при постоянном давлении

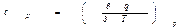
Связь между ними легко устанавливается из первого закона термодинамики

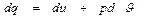или

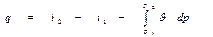
Если теплота подводится при постоянном объеме, то 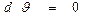, а следовательно,

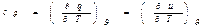
Если теплота подводится при постоянном давлении, то

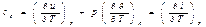
В идеальном газе силы взаимодействия между молекулами отсутствуют, а объём, который они занимают, также равен нулю, т.е. внутренняя энергия u состоит только из кинетической энергии движения молекул 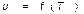и, значит, не зависит ни от объема, ни от давления:

,

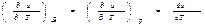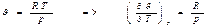
Окончательно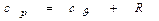

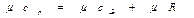
Молекулярно-кинетическая теория теплоемкости

Численные значения теплоемкости идеальных газов могут быть получены из основного уравнения кинетической теории газов:

Умножая обе части этого уравнения на объем одного киломоля 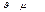, получаем

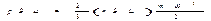
где 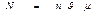– число молекул в одном киломоле газа (число Авогадро, 6,023×10²⁶).

Если молекулы газа представить себе в виде материальных точек, могущих совершать только поступательное движение, то внутренняя энергия одного киломоля будет равна

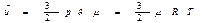
Материальная точка имеет 3 степени свободы, следовательно, на каждую из них в одном киломоле газа приходится внутренняя энергия, равная .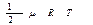

При постоянном объеме подвод теплоты не вызывает совершения работы газом, поэтому 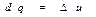, и мольная изохорная теплоёмкость:

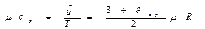
Мольная изобарная теплоёмкость: