Механические колебания и волны.
Литература:
2. с. 7-38.; 3. с. 8-19; 5. с. 43-62; 6. с. 54-66; 7. Глава 5, с.71- 91;
10. с. 63-65; 11. Лекции 2, с. 8-14; 12 с. 3-13; 13. Лекции 6, 7.
ВОПРОСЫ ДЛЯ САМОПОДГОТОВКИ.
1. Гармонические колебания (смещение, амплитуда, фаза, скорость и ускорение колеблющейся точки).
2. Уравнение динамики гармонического колебательного движения.
3. Кинетическая и потенциальная энергия колебательного движения.
4. Затухающие колебания:
А) уравнение динамики свободных затухающих колебаний;
Б) уравнение кинематики свободных затухающих колебаний;
В) декремент затухания;
Г) логарифмический декремент затухания.
5. Вынужденные колебания, Автоколебания. Резонанс.
А) уравнение динамики вынужденных колебаний;
Б) уравнение кинематики вынужденных колебаний;
В) резонанс;
Г) автоколебания.
6. Механические волны.
А) уравнение плоской волны;
Б) поток энергии и интенсивность волны;
В) линейная и групповая скорости волны.
7. Эффект Доплера.
Мотивация цели.
Повторяющиеся движения или изменения состояния называют колебаниями. Всем колебаниям, в независимости от природы, присущи общие закономерности. Колебания распространяются в средах в виде волн.
В живом организме, а так же при диагностике и лечении заболеваний широко распространены процессы с повторением различных состояний и описывающих их параметров. Лучше понять распространение упругих колебаний и волн в сосудах, работу сердца, легких, восприятие звука, распространение биопотенциалов и свойства других колебательных процессов поможет знание основных параметров и закономерностей колебательных движений. Самыми простыми для изучения и понимания являются механические колебания.
Цель занятия изучить основные понятия, законы и закономерности простейших механических колебаний и волн; применять основные положения теории колебаний и волн к процессам, протекающим в организме, а также при диагностике и лечении заболеваний.
Подготовка к практическому занятию.
Изучить по рекомендованной литературе, уметь объяснять и пояснять примерами следующие вопросы:
I. Основные понятия.
Колебания и волны. Свободные колебания. Параметры колебательных движений: смещение, амплитуда, фаза, циклическая частота, и др.
II. Основные законы теории колебаний и волн.
1.Уметь выводить уравнения динамики и кинематики свободных гармонических незатухающих и затухающих колебаний, а так же вынужденных колебаний. Знать основные параметры колебательного и волнового движения.
2. Энергия колеблющейся точки. Энергия волны. Поток энергии. Интенсивность волны.
3. Автоколебательные процессы.
4. Явления резонанса.
5. Эффект Доплера.
Теоретические сведения.
I. Основные понятия.
Колебания - периодически повторяющиеся процессы или явления.
Смещение – отклонение колеблющейся точки от положения равновесия.
Амплитуда – максимальное отклонение колеблющейся точки от положения равновесия или максимальное смещение.
Фаза колебаний – параметр, однозначно определяющий положение колеблющейся точки в пространстве. Условно фаза это угол поворота радиус-вектора 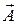 (амплитуды).
(амплитуды).
Циклическая частота– угловая скорость вращения радиус-вектора 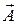 . Угол поворота радиус-вектора
. Угол поворота радиус-вектора 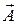 за цикл (период).
за цикл (период).
Период – время одного полного колебания, время цикла.
Частота – число полных колебаний за единицу времени.
Скорость – первая производная смещения по времени ν=dх/dt.
Ускорение– первая производная скорости по времени α=dν/dt или вторая производная смещения по времени α=d2х/dt2 .
Квазиупругая сила – сила, действие которой аналогично действию силы упругости, определяемой законом Гука (F=-kx).
Математический маятник – материальная точка массой m, подвешенная на тонкой невесомой нити длиной ℓ.
Пружинный маятник - материальная точка массой m,прикрепленная к невесомой пружине жесткостью k.
Физический маятник – протяженное тело различной формы и размеров, совершающее колебания около точки подвеса или опоры..
Свободные колебания – колебания, происходящие в системе за счет однократного сообщения ей энергии.
Гармонические колебания– колебания, происходящие по закону sin или cos. (х=Аcos(ωt+φ0))
Затухающие колебания – колебания с уменьшающейся амплитудой.
Вынужденные колебания – колебания под действием внешнего изменяющегося фактора (силы).
Резонанс – явление достижения максимальной амплитуды вынужденных колебаний при заданных ω0 – циклической частоты собственных колебаний и β – коэффициента затухания.
Декремент затухания – отношение двух последовательных амплитуд, разделенных интервалом времени, равном периоду колебаний ( 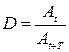 ).
).
Логарифмический декремент затухания – натуральный логарифм отношения двух последовательных амплитуд, разделенных интервалом времени, равном периоду колебаний. Логарифмический декремент затухания - натуральный логарифм декремента затухания. ( 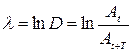 ).
).
Автоколебания – незатухающие колебания, существующие в системе с затуханием при отсутствии переменного внешнего воздействия.
Механическая волна – механическое возмущение, распространяющееся в среде и несущее энергию.
Фронт волны – поверхность, в которой все точки волны колеблются в одинаковой фазе.
Плоская волна – волна, фронт которой является плоским.
Фазовая скорость – скорость распространения фиксированной фазы колебаний.
Групповая скорость – скорость группы синусоидальных волн.
Поток энергии – средняя энергия, переносимая волной в единицу времени ( 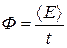 ).
).
Интенсивность – поток энергии через единичную площадь, расположенную перпендикулярно направлению распространения волны ( 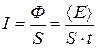 ).
).
Эффект Доплера – изменение частоты волн, воспринимаемых приемником (наблюдателем), вследствие относительного движения источника и приемника волн. ( 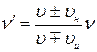 ).
).
II. Основные законы теории колебаний и волн.
1. Гармонические колебания.
Гармонические колебания – колебания, происходящие по гармоническому закону (закону синуса или косинуса).
Х = А sin (ωt + φ0). (1)
В уравнении 1: А - амплитуда колебаний; (ωt + φ0) – фаза колебаний;
φ0- начальная фаза; ω – круговая (циклическая) частота.


вектора 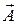 , фаза – угол между вектором
, фаза – угол между вектором 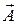 и осью Х.
и осью Х.
Рассмотрим колебания горизонтального пружинного маятника. Один
|
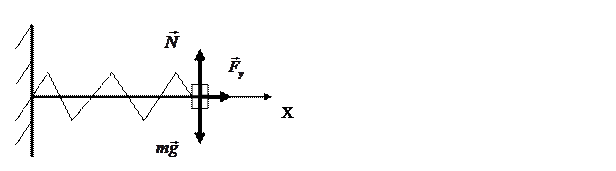
Запишем это уравнение в проекции на ось Х: ma=Fу или m(d2x/dt2)= -kx
Разделим обе части уравнения на m и перенесем все слагаемые в левую часть уравнения (d2x/dt2 )+ (k/m)x=0 . Введем обозначения (k/m)=ω02, где ω0 - циклическая частота собственных колебаний. Перепишем уравнение
(d2x/dt2 ) + ω02 x=0 (2)
Получили уравнение второго порядка гармонических колебаний, так как
решением его является уравнение гармонических колебаний
Х=Аcos(ω0t + φ0)
Если подставить в уравнение 2 значения d2x/dt2 (d2x/dt2 =-А ω02 cos(ω0t + φ0)) и X (Х=Аcos(ω0t + φ0) ), то получим -А ω02 cos(ω0t+φ0) +А ω02 cos(ω0t+φ0)=0.
Следовательно Х=Аcos(ω0t + φ0) является решением уравнения 2.
Круговая частота ω связана с частотой колебаний υ соотношением υ= ω/2π. Период колебаний Т=1/υ =2π/ω. Для пружинного маятника Т=2π 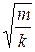 , для математического T =2π
, для математического T =2π 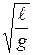 , для физического маятника
, для физического маятника 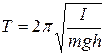 (I - момент инерции тела относительно оси, m –масса маятника, h – расстояние между центром тяжести и осью вращения).
(I - момент инерции тела относительно оси, m –масса маятника, h – расстояние между центром тяжести и осью вращения).
Скорость материальной точки колеблющейся по гармоническому закону: ν = dx/dt= - Aωsin(ωt + φ0) (3); ν = - νmax sin(ωt + φ0)=
νmax cos((ωt + φ0)+π/2), где νmax= Aω.
Фаза скорости больше фазы смещения на π/2.
Ускорение а = dν/dx =- Aω2 cos(ωt + φ0) (3);
a = - amax cos(ωt + φ0) =amax cos((ωt + φ0) + π) (4), где amax = Aω2.
Ускорение и смещение находятся в противофазе.
Кинетическая энергия колеблющейся материальной точки
Ек = (½)mν2 =(½)m A 2ω 2sin 2(ωt + φ0)
Ек =(½)k A 2sin 2(ωt + φ0) (5), где mω 2=k.
Потенциальная энергия
Еп =(½)к х2 =(½)к А 2cos 2(ωt + φ0) (5)
Полная механическая энергия
Е= Ек+ Еп=(½)k A 2 (sin 2(ωt + φ0)+ cos 2(ωt + φ0)) =(½)k A 2 (6)
При отсутствии сил трения полная механическая энергия сохраняется.
Затухающие колебания.
Действие сил трения существенно изменяет характер движения, колебание становится затухающим. Рассмотрим колебания горизонтального пружинного маятника.
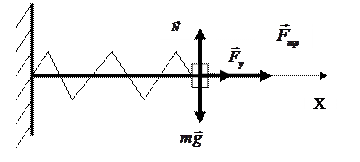
На тело действуют сила тяжести 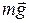 сила упругости пружины
сила упругости пружины 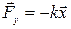 , сила трения
, сила трения 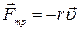 , нормальная реакция опоры
, нормальная реакция опоры 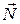 . Запишем 2-й закон Ньютона.
. Запишем 2-й закон Ньютона.
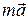 =
= 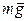 +
+ 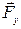 +
+ 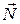 +
+ 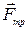 .
.
Запишем это уравнение в проекции на ось Х:
ma=Fу+Fтр или m(d2x/dt2)= -kx – r(dx/dt).
Разделим обе части уравнения на m и перенесем все слагаемые в левую часть уравнения
(d2x/dt2 )+ (r/m) (dx/dt) +(k/m)x=0 .
Введем обозначения (r/m)=2β и (k/m)=ω02, где β - коэффициент затухания, а ω0 - циклическая частота собственных колебаний. Перепишем уравнение
(d2x/dt2 )+ 2β(dx/dt) + ω02 x = 0 (7)
Получили уравнение второго порядка затухающих колебаний. Решение этого уравнения существенно зависит от знака разности ω2= ω02 – β2, где ω циклическая частота затухающих колебаний.
При ω02 – β2>O решение записывается в следующем виде:
X=A0e-βt cos(ωt +φ0) (8), где
(A0e-βt) - амплитуда затухающих колебаний, которая изменяется по экспоненциальному закону.
Период затухающих колебаний Т=2π/ω= 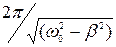 .
.
При очень малом трении (ω02 >> β2) Т=2π/ω0.
Быстрота убывания амплитуды колебаний определяется коэффициентом затухания β: чем больше β, тем сильнее торможение.
На практике степень затухания характеризуют логарифмическим декрементом затухания
λ =ℓn 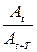 =ℓn
=ℓn 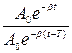 = ℓn e βt= βt
= ℓn e βt= βt
λ= βt (9)
При сильном затухании (β2>ω02) период является мнимой величиной, а колебания апериодическими.
3. Вынужденные колебания. Резонанс. Автоколебания.
Вынужденными называют колебания, которые возникают в системе при участии внешних сил, изменяющихся по периодическому закону.
Пусть на горизонтальный пружинный маятник помимо указанных выше сил действует вынуждающая сила, изменяющаяся по закону
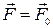 cos ωt. Тогда по второму закону Ньютона:
cos ωt. Тогда по второму закону Ньютона:
|
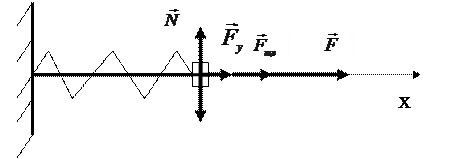
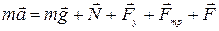
В проекции на ось Х ma = Fу+Fтр+F или m(d2x/dt2)= -kx – r(dx/dt) + F0 cos ωt. Разделим на m и введем обозначения f0=F0/m, 2β=r/m; ω02 =k/m.
Получаем: (d2x/dt2) +(r/m)(dx/dt) +(k/m)x = f0 cos ωt.
(d2x/dt2 )+ 2β(dx/dt) + ω02 x= f0 cos ωt. (10)
Решением этого уравнения является сумма 2-х слагаемых. Одно из них X=A0e-βtcos(ωt +φ0). Это уравнение затухающих колебаний играет роль только при установлении колебаний. Со временем им можно пренебречь.
Другое слагаемое X=A cos(ωt +φ0) (11) описывает смещение материальной точки в установившихся вынужденных колебаниях.
А= f0/ 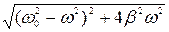 (12); tg φ0=-2βω/(ω 2 – ω02)(13).
(12); tg φ0=-2βω/(ω 2 – ω02)(13).
Как видно, вынужденное колебание так же является гармоническим. Частота его равна частоте вынуждающей силы. Амплитуда вынужденных колебаний прямо пропорциональна амплитуде вынуждающей силы и имеет сложную зависимость от коэффициента затухания β, а так же ω и ω0.
Если знаменатель имеет минимальное значение, то амплитуда А имеет максимальное. Это явление резонанса. Резонансная частота 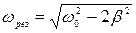 (14), амплитуда Арез=f0/2β
(14), амплитуда Арез=f0/2β 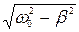 (15). При отсутствии сопротивления (β≈0) Арез→ ∞ и ωрез→ω0
(15). При отсутствии сопротивления (β≈0) Арез→ ∞ и ωрез→ω0
Существуют колебательные системы, которые сами регулируют периодическое восполнение затраченной энергии. Незатухающие колебания, существующие в таких системах, называются автоколебаниями. Амплитуда и частота автоколебаний зависит от свойств самой системы. Примеры: в технике часы, генераторы электромагнитных колебаний; в биологии – сердце, легкие и т. д..
4.Механические волны.
Уравнение плоской волны S= A cos(ω(t-x/ν)) (16), где S – смещение, колеблющейся точки, ω – циклическая частота колебаний; t- время распространения волны; x- координата точки, до которой дошла волна,
ν – скорость ее распространения.
Длина волны λ– расстояние между двумя точками, фазы колебания которых в одно и то же время отличаются на 2π или - путь, пройденный волной за время равное периоду колебаний. λ=Τν (17).
Фазовойскоростью называют скорость распространения фазы колебаний. Если реальная волна является группой гармонических волн, то говорят о групповой скорости.
Потоком энергии называют энергию, переносимую через поверхность в единицу времени. Ф=dE/dt (18) [Ф] = Вт
Ф = 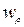 sν -
sν - 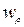 = Е/V– объемная плотность энергии.
= Е/V– объемная плотность энергии.
Плотность потока энергии I = Ф/S = wρν => I = wρν, показывает направление распространения волны. Его называют вектором Умова:
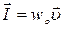 (19)
(19)
Так как Е=(½)k A2 = (½)m ω02 A2, а m=ρv => 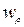 =E / v =
=E / v =
(½)ρ ω02 A2=> I = (½)ρ ω02 A2 ν
5.Эффект Доплера.
При относительном движении источника и приемника механических волн (звука) происходит изменение частоты волны воспринимаемой приемником (наблюдателем). Это явление получило название эффект Доплера.
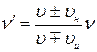 , где -
, где - 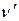 воспринимаемая приемником частота;
воспринимаемая приемником частота;
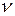 – излучаемая частота;
– излучаемая частота; 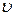 – скорость волны (звука);
– скорость волны (звука); 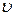 н – скорость наблюдателя;
н – скорость наблюдателя; 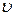 и – скорость источника. Верхние знаки применяют при сближении объектов, а нижние при их удалении.
и – скорость источника. Верхние знаки применяют при сближении объектов, а нижние при их удалении.
В медицине эффект Доплера используется для определения скорости кровотока, скорости движения клапанов и стенок сердца (доплеровская эхокардия).
Пример: определение скорости кровотока.
Генератор ультразвука совмещают с приемником (техническая система) и помещают в сосуд с движущейся кровью (аорту, артерию и т. Д.).
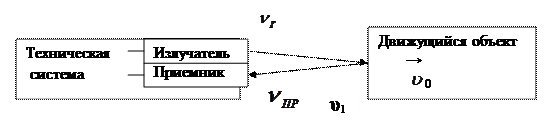
В среде движется объект (эритроциты) со скоростью ν0 равной скорости кровотока и направленной к технической системе. Генератор излучает УЗ с частотой υг , распространяющийся со скоростью 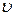 0ν. Объект воспринимает уже частоту υ1 =((ν +
0ν. Объект воспринимает уже частоту υ1 =((ν + 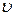 0 )/ν)υг и отражает ее назад к технической системе. Приемник воспринимает частоту
0 )/ν)υг и отражает ее назад к технической системе. Приемник воспринимает частоту
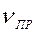 =(ν/ (ν –
=(ν/ (ν – 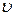 0))υ1 ==(ν/ (ν –
0))υ1 ==(ν/ (ν – 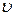 0)) ((ν +
0)) ((ν + 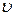 0 )/ν) υг =((ν +
0 )/ν) υг =((ν + 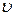 0 )/(ν –
0 )/(ν – 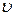 0)) υг
0)) υг
Доплеровский сдвиг частот ∆υ
∆υ=υD = 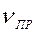 – υг=((ν +
– υг=((ν + 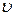 0 )/(ν –
0 )/(ν – 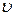 0)) υг – υг = (2
0)) υг – υг = (2 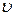 0 /(ν –
0 /(ν – 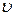 0))υг. При определении скорости кровотока ν >>
0))υг. При определении скорости кровотока ν >> 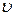 0 => ∆υ=υD = (2
0 => ∆υ=υD = (2 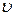 0 /ν)υг
0 /ν)υг
Задачи для самостоятельного решения.
1. Дифференциальное уравнение колебаний имеет вид:
0.2 d2x/dt2 + 0,6 dx/dt + 0,8 x =0. Найти коэффициент затухания β, циклическую частоту ω и период колебаний Т.
2. Определить частоту собственных колебаний ноги человека, рассматривая ее как физический маятник, приведенная длина которого
ℓ=40 см. Приведенная длина - это длина математического маятника ℓ, период колебаний которого равен периоду колебаний физического маятника.
3. Горизонтальный пружинный маятник (тело массойm=1кг, прикрепленное к пружине жесткостью k=10 Н/м) совершает колебательные движения. Начальная амплитуда колебаний А0=1см. Записать дифференциальное уравнение колебаний, а также решение этого уравнения.
4. Известно, что человеческое ухо воспринимает упругие волны в интервале от 20 Гц до 20 кГц. Каким длинам волн соответствует этот интервал в воздухе? Скорость звука в воздухе 340 м/с.
5. Определить разность фаз в пульсовой волне между двумя точками артерии, расстояние между которыми 20 см. Скорость пульсовой волны
10 м/с. Колебания сердца считать гармоническими с частотой 1,2 Гц.
6. Скорость движения эритроцита в артерии равна 0,3 м/с. Скорость ультразвука – 1500 м/с, частота - 100 кГц. Найти доплеровский сдвиг частоты, если эритроцит движется навстречу технической системе.
Образец решения задачи.
1) Условие задачи.
Горизонтальный пружинный маятник (тело массойm=100г, прикрепленное к пружине жесткостью k=1 Н/м) совершает колебательные движения в вязкой среде. Сила сопротивления прямо пропорциональна скорости. Коэффициент пропорциональности r=0,01 Нс/м. На колебательную систему действует внешняя вынуждающая сила F=5 sin (πt/2). Записать дифференциальное уравнение колебаний, а также решение этого уравнения. При какой частоте внешней вынуждающей силы в системе наступит резонанс?
Анализ условия задачи.
По условию задачи дано тело, которое совершает колебательные движения. Будем считать тело материальной точкой. Массой пружины и силой трения между опорой и телом пренебрежем. Укажем действующие 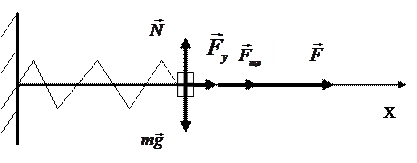
силы. Необходимо записать уравнения динамики (X(m,k,r,t,F)) и кинематики (Х(t)) вынужденных колебаний, а также определить величину резонансной частоты (ωрез).
Запишем условие и решение задачи в символической форме.
|
|

2β=(0,01Н•с/м)/ 0,1кг=0,1(кг• м •с)/(с2•м •кг)=0,1с-1; β=0,05 с-1
ω02 = (1 Н/м)/0,1кг=10 кг м/м с2кг=10 с-2; ω0=3,16 с-1
f0= 5 Н/0,1 кг = (50) кг м/с2кг=50 м/с2
(d2x/dt2 )+ 0,1(dx/dt) + 10 x= (50) sin (πt/2)
Решением этого уравнения является
Х = А sin(ωt + φ0 ) ω=π/2 => Х= А sin(πt/2+φ0)
А= f0/ 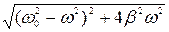 ; tg φ0=-2βω/(ω 2 – ω02)
; tg φ0=-2βω/(ω 2 – ω02) 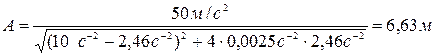
tg φ0=- 2•0,05 с-1 •1,57 с-1/(2,46 с-2-10 с-2)=0,02082
φ0 =1,3 рад
Х=6,63 sin(1,57 • t +1,3)
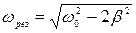
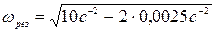 =3,16 рад/с
=3,16 рад/с
Ответ: 1) (d2x/dt2 )+ 2β(dx/dt) + ω02 x= f0 sin ωt;
2) (d2x/dt2 )+ 0,1(dx/dt) + 10 x= (50) sin (1,57•t);
3) Х = А sin(ωt + φ0)
4) Х=6,63 sin(1,57 • t +1,3)
5) ωрез= 3,16 рад/с
Тесты для самоконтроля.
Уровень.

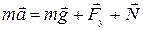 (1)
(1)