Взаимодействие тел. Сила. Второй закон Ньютона.

План ответа

1. Взаимодействие тел.

2. Виды взаимодействия.

3. Сила.

4. Силы в механике.

Простые наблюдения и опыты, например с тележками (рис. 1), приводят к следующим качественным

заключениям: а) тело, на ко­торое другие тела не действуют, со­храняет свою скорость неизмен­ной; б) ускорение тела возникает под действием других тел, но зави­сит и от самого тела;

в) действия тел друг на друга всегда носят ха­рактер взаимодействия.

Эти выво­ды подтверждаются при наблюде­нии явлений в природе, технике, космическом пространстве только в инерциальных системах отсчета.

Взаимодействия отличаются друг от друга и количественно, и качественно.

Например, ясно, что чем больше деформируется пружи­на, тем больше взаимодействие ее витков. Или чем ближе два одно­именных заряда, тем сильнее они будут притягиваться.

В простей­ших случаях взаимодействия количественной характеристикой является сила.

Сила — причина ускорения тел по отношению к инерциальной системе отсчета или их деформации.

Сила — это век­торная физическая величина, яв­ляющаяся мерой ускорения, при­обретаемого телами при взаимо­действии.

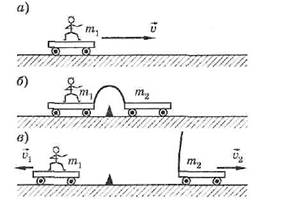Рис. 1

Сила характеризуется: а) модулем; б) точкой приложе­ния; в) направлением.

Единица силы — ньютон.

1 нью­тон — это сила, которая телу мас­сой 1 кг сообщает ускорение 1 м/с в направлении действия этой си­лы, если другие тела на него не действуют.

Равнодействующей не­скольких сил называют силу, дей­ствие которой эквивалентно дейст­вию тех сил, которые она заменя­ет. Равнодействующая является векторной суммой всех сил, прило­женных к телу.

R^g= F^g₁ + F^g₂ + ... + F^g_n.

На основании опытных данных были сформулированы законы Нью­тона.

Второй закон Ньютона. Уско­рение, с которым движется тело, прямо пропорционально равнодей­ствующей всех сил, действующих на тело, обратно пропорционально его массе и направлено так же, как и равнодействующая сила:

а^→ = F^→/т.

Для решения задач закон часто записывают в виде: F^→=m a^→.

Билет №13 Импульс тела. Закон сохра­нения импульса.

План ответа

1.Импульс тела.

2.Закон сохранения импульса.

3.Реактивное движение.

Покой и движе­ние относительны, скорость тела зависит от выбора системы отсче­та; по второму закону Ньютона не­зависимо от того, находилось ли тело в покое или двигалось, изме­нение скорости его движения мо­жет происходить только при дей­ствии силы, т. е. в результате взаи­модействия с другими телами. Существуют величины, ко­торые могут сохраняться при взаи­модействии тел. Такими величина­ми являются энергия и импульс.

Импульсом тела называют век­торную физическую величину, яв­ляющуюся количественной харак­теристикой поступательного движе­ния тел. Импульс обозначается р^→.

Единица измерения импульса р^→ — кг • м/с.

Импульс тела равен про­изведению массы тела на его ско­рость: р^→ = т υ^→.

Направление векто­ра импульса р^→ совпадает с направ­лением вектора скорости тела υ^→ (рис. 1).

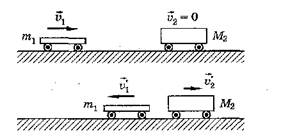Рис. 1

Для импульса тел выполняется закон сохранения, который спра­ведлив только для замкнутых фи­зических систем.

В механике замкну­той называют систему, на которую не действуют внешние силы или действие этих сил скомпенсирова­но.

В этом случае р^→₁ = р^→₂, где р^→₁ — начальный импульс системы, а р^→₂ — конечный.

В случае двух тел, входящих в систему, это выраже­ние имеет вид т₁υ^→₁ + т₂υ^→₂ = m₁υ^→₁' + m₂υ^→₂' , где т₁ и т₂ — массы тел, а υ^→₁ и υ^→₂ — скорости до взаимодей­ствия, υ^→₁' и υ^→₂' — скорости после взаимодействия.

Эта формула закона сохранения им­пульса: импульс замкнутой физи­ческой системы сохраняется при любых взаимодействиях, происходящих внутри этой системы.

. В слу­чае незамкнутой системы импульс тел системы не сохраняется.

Одна­ко если в системе существует на­правление, по которому внешние силы не действуют или их дейст­вие скомпенсировано, то сохраня­ется проекция импульса на это на­правление.

Если время взаимодействия мало (выстрел, взрыв, удар), то за это время даже в случае незамкнутой системы внеш­ние силы незначительно изменяют импульсы взаимодействующих тел.

Экспериментальные исследова­ния взаимодействий различных тел — от планет и звезд до атомов и элементарных частиц — показа­ли, что в любой системе взаимо­действующих тел при отсутствии действия со стороны других тел, не входящих в систему, или равенст­ве нулю суммы действующих сил геометрическая сумма импульсов тел действительно остается неиз­менной.

В механике закон сохранения импульса и законы Ньютона связа­ны между собой.

Если на тело мас­сой т в течение времени t действует сила и скорость его движения изме­няется от υ^→₀ до υ^→,то ускорение дви­жения а^→ тела равно а^→ = (υ^→ - υ^→₀)/t.

На основании второго закона Ньютона

для силы F^→ можно записать F^→ = та^→ = т(υ^→ - υ^→₀) / t, отсюда следует

F^→t = mυ^→ - mυ^→₀.

F^→t — векторная физическая ве­личина, характеризующая дейст­вие на тело силы за некоторый промежуток времени называется импульсом си­лы.Единица импульса в СИ — 1Н · с.

Закон сохранения импульса ле­жит в основе реактивного движе­ния.

Реактивное движение— этотакое движение тела, которое воз­никает после отделения от тела его части.

Пример: тело массой т покоилось. От тела отделилась какая-то его часть т₁ со скоростью υ^→₁. Тогда ос­тавшаяся часть придет в движение в противоположную сторону со скоростью υ^→₂, масса оставшейся части т₂. Действительно, сумма импульсов обеих частей тела до от­деления была равна нулю и после разделения будет равна нулю:

т₁υ^→₁ + m₂υ^→₂ =0, отсюда υ^→₁ = -m₂υ^→₂ / m₁.

К. Э. Циолковский разработал теорию полета те­ла переменной массы (ракеты) в однородном поле тяготения и рас­считал запасы топлива, необходи­мые для преодоления силы земно­го притяжения.

Техниче­ские идеи Циолковского находят применение при создании совре­менной ракетно-космической тех­ники. Движение с помощью реак­тивной струи по закону сохране­ния импульса лежит в основе гидрореактивного двигателя. В ос­нове движения многих морских моллюсков (осьминогов, медуз, кальмаров, каракатиц) также ле­жит реактивный принцип.

Билет № 17

Закон всемирного тяготе­ния. Сила тяжести. Вес тела. Не­весомость.

План ответа

1. Силы гравитации.

2. Закон всемирного тяготения.

3. Физический смысл гравитацион­ной постоянной.

4. Сила тяжести.

5. Вес тела, перегрузки.

6. Невесомость.

Исаак Ньютон выдвинул пред­положение, что между любыми те­лами в природе существуют силы взаимного притяжения.

Эти силы называют силами гравитации,или силами всемирного тяготе­ния.Сила всемирного тяготения проявляется в Космосе, Солнеч­ной системе и на Земле. Ньютон вывел формулу :

т₁ · т₂

F = G ————, где G — коэффициент пропорциональности, на­зывается гравитационной

R²

Постоянной.

Закон всемирного тяготения : между любыми мате­риальными точками существует сила взаимного притяжения, пря­мо пропорциональная произведе­нию их масс и обратно пропор­циональная квадрату расстояния между ними, действующая по линии, соединяющей эти точки.

Физический смысл гравитаци­онной постоянной вытекает из за­кона всемирного тяготения.

Если т₁ = т₂= 1 кг, R = 1 м, то G = F, т. е. гравитационная постоянная равна силе, с которой притяги­ваются два тела по 1 кг на рас­стоянии 1 м. Численное значение: G = 6,67 • 10^-11 Н • м²/кг². Силы всемирного тяготения действуют между любыми телами в природе, но ощутимыми они становятся при больших массах. Закон всемирного тяготения выполняет­ся только для материальных точек и шаров (в этом случае за расстоя­ние принимается расстояние меж­ду центрами шаров).

Частным видом силы всемирно­го тяготения является сила притя­жения тел к Земле (или к другой планете). Эту силу называют силой тяжести.

Под действием этой силы все тела приобретают ускорение свободного падения. В соответст­вии со вторым законом Ньютона g = F_T /m, следовательно, F_Т = тg.

Сила тяжести всегда направлена к центру Земли.

На поверхности Земли ускорение сво­бодного падения равно 9,831 м/с².

Ве­сом теланазывают силу, с которой тело давит на опору или подвес в результате гравитационного при­тяжения к планете (рис. 1).

Вес те­ла обозначается p^→. Единица веса — 1 Н. Так как вес равен силе, с кото­рой тело действует на опору, то в соответствии с третьим законом Ньютона по величине вес тела ра­вен силе реакции опоры. Поэтому, чтобы найти вес тела, необходимо найти, чему равна сила реакции опоры.

Рис. 1 Рис. 2

Рассмотрим случай, когда тело вместе с опорой не движется. В этом случае сила реакции опоры и вес тела равен силе тяжести (рис. 2):

Р^→= N^→ = тg^→.

В случае движения тела верти­кально вверх вместе с опорой с ус­корением по второму закону Нью­тона можно записать тg^→ + N^→ = та^→ (рис. 3, а).

В проекции на ось ОХ:

-тg + N = та, отсюда

N = т(g + а).

При движении вертикально вверх с ускорением вес тела увеличивается и находит­ся по формуле Р = т(g + а).

Увеличение веса тела, вызван­ное ускоренным движением опоры или подвеса, называют перегруз­кой.

Действие перегрузки испы­тывают на себе космонавты, водители ав­томобилей при резком торможе­нии.

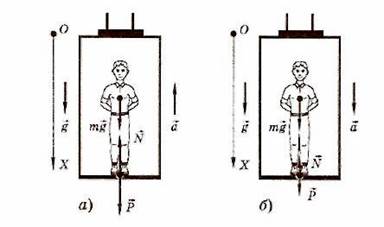Рис. 3

Если тело движется вниз по вер­тикали,

тg^→ + N^→ = та^→; тg — N = та; N = т(g - а); Р = т(g - а),

т. е. вес при движении по вертикали с ус­корением будет меньше силы тя­жести (рис. 3, б).

Если тело свободно падает, в этом случае Р = (g – g)m =0

Состояние тела, в котором его вес равен нулю, называют неве­сомостью. Состояние невесомости наблюдается в самолете или кос­мическом корабле при движении с ускорением свободного падения независимо от направления и зна­чения скорости их движения.

Билет №24 Превращение энергии при механических колебаниях. Сво­бодные и вынужденные колеба­ния. Резонанс.

План ответа

1. Определение колебательного дви­жения.

2. Свободные колебания.

3. Превращения энергии.

4. Вынужденные колебания. Механическими колебаниями

называют движения тела, повто­ряющиеся точно или приблизи­тельно через одинаковые про­межутки времени. Основными характеристиками механических колебаний являются: смещение, амплитуда, частота, период. Сме­щение— это отклонение от поло­жения равновесия. Амплитуда — модуль максимального отклоне­ния от положения равновесия. Частота — число полных колеба­ний, совершаемых в единицу вре­мени. Период — время одного полного колебания, т. е. мини­мальный промежуток времени, че­рез который происходит повторе­ние процесса. Период и частота связаны соотношением: ν = 1/Т.

Простейший вид колебательно­го движения — гармонические ко­лебания, при которых колеблю­щаяся величина изменяется со временем по закону синуса или ко­синуса (рис. 1).

Свободныминазывают колеба­ния, которые совершаются за счет первоначально сообщенной энер­гии при последующем отсутствии внешних воздействий на систему, совершающую колебания. Напри­мер, колебания груза на нити (рис. 2).

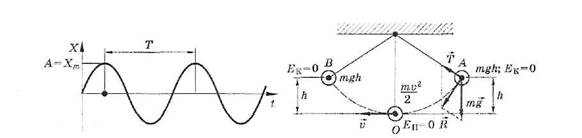Рис. 1 Рис. 2

Рассмотрим процесс превраще­ния энергии на примере колебаний груза на нити (см. рис. 2).

При отклонении маятника от положения равновесия он подни мается на высоту h относительно нулевого уровня, следовательно, в точке А маятник обладает потен­циальной энергией тgh. При дви­жении к положению равновесия, к точке 0, уменьшается высота до нуля, а скорость груза увеличива­ется, и в точке 0 вся потенциаль­ная энергия тgh превратится в ки­нетическую энергию тυ²/2. В по­ложении равновесия кинетическая энергия имеет максимальное зна­чение, а потенциальная энергия минимальна. После прохождения положения равновесия происходит превращение кинетической энер­гии в потенциальную, скорость ма­ятника уменьшается и при максимальном отклонении от положе­ния равновесия становится равной нулю. При колебательном движе­нии всегда происходят периоди­ческие превращения его кинетиче­ской и потенциальной энергии.

При свободных механических колебаниях неизбежно происходит потеря энергии на преодоление сил сопротивления. Если колебания происходят под действием перио­дической внешней силы, то такие колебания называют вынужден­ными. Например, родители раска­чивают ребенка на качелях, пор­шень движется в цилиндре двига­теля автомобиля, колеблются нож электробритвы и игла швейной машины. Характер вынужденных колебаний зависит от характера действия внешней силы, от ее ве­личины, направления, частоты действия и не зависит от размеров и свойств колеблющегося тела. На­пример, фундамент мотора, на ко­тором он закреплен, совершает вы­нужденные колебания с частотой, определяемой только числом обо­ротов мотора,- и не зависит от раз­меров фундамента.

При совпадении частоты внеш­ней силы и частоты собственных колебаний тела амплитуда вынуж­денных колебаний резко возраста­ет. Такое явление называют меха­ническим резонансом. Графически зависимость вынужденных коле­баний от частоты действия внеш­ней силы показана на рисунке 3.

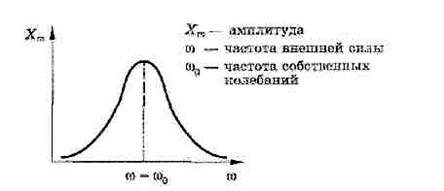Рис. 3

Явление резонанса может быть причиной разрушения машин, зда­ний, мостов, если собственные их частоты совпадают с частотой пе­риодически действующей силы. Поэтому, например, двигатели в автомобилях устанавливают на специальных амортизаторах, а во­инским подразделениям при дви­жении по мосту запрещается идти «в ногу».

При отсутствии трения ампли­туда вынужденных колебаний при резонансе должна возрастать со временем неограниченно. В реаль­ных системах амплитуда в устано­вившемся режиме резонанса опре­деляется условием потерь энергии в течение периода и работы внеш­ней силы за то же время. Чем меньше трение, тем больнее ампли­туда при резонансе.

Билет №16

Конденсаторы. Электроем­кость конденсатора. Применение конденсаторов.

План ответа

1. Определение конденсатора.

2. Обозначение.

3. Электроемкость конденсатора.

4. Электроемкость плоского кон­денсатора.

5. Соединение конденсаторов.

6. Применение конденсаторов.

Для накопления значительных количеств разноименных электри­ческих зарядов применяются кон­денсаторы.

Конденсатор— это сис­тема двух проводников (обкладок), разделенных слоем диэлектрика, толщина которого мала по сравне­нию с размерами проводников.

Пример, две плоские метал­лические пластины, расположенные параллельно и разделенные диэлектриком, образуют плоский конденсатор.

Если пластинам плос­кого конденсатора сообщить рав­ные по модулю заряды противопо­ложного знака, то напряженность между пластинами будет в два раза больше, чем напряженность одной пластины. Вне пластин напряжен­ность равна нулю.

Обозначаются конденсаторы на схемах так:

Электроемкостью конденсато­ра называют величину, равную от­ношению величины заряда одной из пластин к напряжению между ними. Электроемкость обозначает­ся C.

По определению С = q/U. Еди­ницей электроемкости является фарад (Ф).

1 фарад — это электро­емкость такого конденсатора, на­пряжение между обкладками ко­торого равно 1 вольту при сообще­нии обкладкам разноименных зарядов по 1 кулону.

Электроемкость плоского кон­денсатора находится по формуле:

S

C = ε ε₀ — ,

d

где ε₀ — электрическая постоян­ная, ε — диэлектрическая посто­янная среды, S — площадь об­кладки конденсатора, d — рас­стояние между обкладками (или толщина диэлектрика).

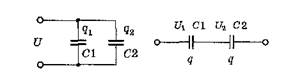
Если конденсаторы соединяют­ся в батарею, то при параллельном соединении С_O = С₁ + С₂ (рис.1). При последовательном соедине­нии

1 1 1

— = — + — ( рис. 2).

C_O C₁ C₂

В зависимости от типа диэлек­трика конденсаторы бывают воз­душные, бумажные, слюдяные.

Конденсаторы применяются для накопления электроэнергии и использования ее при быстром раз­ряде (фотовспышка), для разделе­ния цепей постоянного и перемен­ного тока, в выпрямителях, ко­лебательных контурах и других радиоэлектронных устройствах.

Билет №15

Работа и мощность в цепи постоянного тока. Электродвижу­щая сила. Закон Ома для полной цепи.

План ответа

1. Работа тока.

2. Закон Джоуля—Ленца.

3. Электродвижущая сила.

4. Закон Ома для полной цепи.

В электрическом поле из фор­мулы определения напряжения

U = А / q

то для расчета работы переноса электрического заряда

А = U q так как для тока заряд q = I t

то работа тока:

A = UIt или A = I²Rt = U² / R · t

Мощность по определению N = А / tследовательно, N = UI = I²R = U²/R

закон Джоуля—Ленца: При прохождении тока по проводнику количество теплоты, выделившейся в проводнике, прямо пропорционально квадра­ту силы тока, сопротивлению проводника и времени прохожде­ния тока, Q = I²Rt.

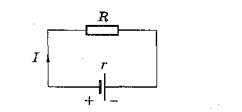Рис. 1

Полная замкнутая цепь пред­ставляет собой электрическую цепь, в состав которой входят внешние сопротивления и источ­ник тока (рис.1).

Как один из участков цепи, источник тока об­ладает сопротивлением, которое называют внутренним, r.

Для того чтобы ток проходил по замкнутой цепи, необходимо, что­бы в источнике тока зарядам сооб­щалась дополнительная энергия, она берется за счет работы по пере­мещению зарядов, которую про­изводят силы неэлектрического происхождения (сторонние силы) против сил электрического поля.

Источник тока характеризуется ЭДС — элек­тродвижущая сила источника.

ЭДС — характеристика источ­ника энергии неэлектрической природы в электрической цепи, необходимого для поддержания в ней электрического тока.

ЭДС из­меряется отношением работы сто­ронних сил по перемещению вдоль замкнутой цепи положительного заряда к этому заряду

Ɛ = A_СТ / q.

Пусть за время t через попереч­ное сечение проводника пройдет электрический заряд q.

Тогда рабо­ту сторонних сил при перемещении заряда можно записать так: А_СТ = Ɛ q.

Согласно определению силы тока q=I t,

А_СТ = Ɛ I t

При совершении этой работы на внут­реннем и внешнем участках цепи, сопротивления которых R и r, выде­ляется некоторое количество тепло­ты.

По закону Джоуля—Ленца оно равно: Q = I² R t + I² r t

Согласно за­кону сохранения энергии А = Q. Следовательно, Ɛ = IR + Ir.

Произ­ведение силы тока на сопротивле­ние участка цепи часто называют падением напряжения на этом участке.

ЭДС равна сумме падений напряжений на внутреннем и внешнем участках замкнутой цепи. О

I = Ɛ / (R + r).

Эта зависимость называется законом Ома для полной цепи

сила тока в полной цепи прямо пропорциональна ЭДС источника тока и обратно про­порциональна полному сопротив­лению цепи.

При разомкнутой цепи ЭДС равна напряжению на зажи­мах источника и, следовательно, может быть измерена вольтметром.

Билет №12

Взаимодействие заряженных тел. Закон Кулона. Закон сохра­нения электрического заряда.

План ответа

1.Электрический заряд.

2. Взаимодействие заряженных тел.

3. Закон сохранения электрическо­го заряда.

4. Закон Кулона.

5. Диэлектрическая проницаемость.

6. Электрическая постоянная.

7. Направление кулоновских сил.

Законы взаимодействия атомов и молекул объяс­няются на основе строении атома, используя планетарную мо­дель его строения.

В центре атома находится положительно заряжен­ное ядро, вокруг которого враща­ются по определенным орбитам отрицательно заряженные части­цы.

Взаимодействие между за­ряженными частицами называет­ся электромагнитным.

Интенсив­ность электромагнитного взаимодействия определяется физиче­ской величиной — электрическим зарядом,который обозначается q.

Единица электрического заряда — кулон (Кл).

1 кулон — это такой электрический заряд, который, проходя через поперечное сечение проводника за 1 с, создает в нем ток силой 1 А.

Способность элек­трических зарядов как к взаимно­му притяжению, так и к взаимно­му отталкиванию объясняется су­ществованием двух видов зарядов.

Один вид заряда называется положи­тельным, носителем элементарно­го положительного заряда являет­ся протон.

Другой вид заряда назвали отрицательным, его но­сителем является электрон. Эле­ментарный заряд равен е = 1,6 × 10^-19 Кл.

. Электрический заряд не создается и не исчезает, а только переходит от одного тела к друго­му.

Этот факт называется зако­ном сохранения электрического заряда.

В приро­де не возникает и не исчезает электрический заряд одного зна­ка.

Появление и исчезновение электрических зарядов на телах в большинстве случаев объясняется переходами элементарных заря­женных частиц — электронов — от одних тел к другим.

Электризация— это сообщение телу электрического заряда.

Элек­тризация может происходить при соприкосновении (тре­нии) разнородных веществ и при облучении.

При электризации в теле возникает избыток или недос­таток электронов.

В случае избытка электронов тело приобретает отрицательный заряд, в случае недостатка — поло­жительный.

Основной закон электростати­ки был экспериментально установ­лен Шар­лем Кулоном :

мо­дуль силы взаимодействия двух точечных неподвижных электри­ческих зарядов в вакууме прямо пропорционален произведению ве­личин этих зарядов и обратно пропорционален квадрату расстоя­ния между ними.

F = k • q₁ q₂ / r² ,

где q₁ и q₂ — модули зарядов, r — рас­стояние между ними, k — коэффи­циент пропорциональности, зави­сящий от выбора системы единиц, в СИ

k = 9 • 10⁹ Н•м²/Кл².

Величина, показывающая, во сколько раз сила взаимодействия зарядов в вакууме больше, чем в среде, называется диэлектриче­ской проницаемостью средыε.

Для среды с диэлектрической про­ницаемостью ε закон Кулона : F = k • q₁ q₂ /(ε • r²).

Вместо коэффициента kчасто используется коэффициент, на­зываемый электрической посто­янной ε₀.

Электрическая по­стоянная связана с коэффици­ентом kследующим образом:

k = 1/4πε₀ и численно равна ε₀ = 8.85 • 10^-12Кл/Н • м²

С использованием электриче­ской постоянной закон Кулона име­ет вид:

1 q₁q₂

F = ——— • ———

4 π ε₀ r²

Взаимодействие неподвижных электрических зарядов называют электростатическим,или кулоновским, взаимодействием.Кулоновские силы можно изобразить гра­фически (рис. 1).

Кулоновская сила направлена вдоль прямой, соединяющей заря­женные тела. Она является силой притяжения при разных знаках зарядов и силой отталкивания при одинаковых знаках.

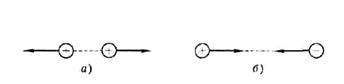Рис. 1

Билет № 14