Простейшие случаи распространения волн при наличии магнитного поля
Кажущаяся простой алгебраическая система векторных уравнений (20.5)—(20.18) оказывается в действительности для произвольного направления распространения довольно громоздкой. Начнем с наиболее простых случаев, в которых магнитное поле не действует на распространение волн. Рассмотрим составляющую векторного уравнения (20.18) вдоль магнитного поля. Поскольку составляющаяj|| вдоль магнитного поля равна (jh), то
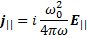 (22.1)
(22.1)
Составляющая уравнения (20.5) вдоль магнитного поля не содержит поперечного поляЕ⊥ в двух случаях: при распространении поперек поля, когда k3 = О, и при распространении вдоль поля, когда k(kE) = k2Е. В этих двух простейших случаях колебания с электрическим полем, параллельным магнитному, отщепляются, т. е. представляют собой независимые ветви колебаний. Магнитное поле на эти ветви колебаний не действует. В гидродинамическом приближении это утверждение является точным. В кинеике, как мы увидим ниже, вблизи циклотронных частот и их обертонов возникают некоторые особенности. Если отвлечься от этих особых точек, то можно сказать, что колебания с электрическим полем вдоль магнитного распространяются вдоль или поперек магнитного поля так же, как и в его отсутствие. Для распространения вдоль магнитного поля уравнение (20.5) сводится к виду
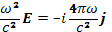 (22.2)
(22.2)
что после подстановки формулы (22.1) дает
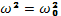 (22.3)
(22.3)
Это значит, что колебания, поляризованные вдоль магнитного поля и распространяющиеся вдоль него, представляeт собой электростатические плазменные колебания, о которых мы уже говорили. Если пренебречь тепловым движением, то эти колебания возможны только на одной фиксированной частоте, которая равна плазменной частоте ω0. При учете теплового движения получается дисперсионное уравнение для плазменных волн, которое мы рассмотрим в следующей главе. Для волн, распространяющихся поперек магнитного поля, но поляризованных вдоль него, уравнение (20.5) сводится к виду
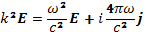 (22.4)
(22.4)
что при подстановке выражения (22.1) дает дисперсионное уравнение
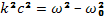 (22.5)
(22.5)
Оно тождественно с уравнением (21.4), описывающим распространение электромагнитных волн в плазме. Распространение возможно только при частотах выше плазменной. Ниже плазменной частоты волновое число становится мнимым, т. е. волна отражается от границы плазмы. На этом основаны микроволновое зондирование плазмы для определения ее концентрации и отражение радиоволн от ионосферы, делающее возможным дальнюю радиосвязь по атмосферному волноводу.
Фазовая и групповая скорости выражаются так же, как и в отсутствие магнитного поля, т. е. формулами (21.5) и (21.6).
Рассмотренные типы колебаний, поляризованные вдоль магнитного поля и распространяющиеся вдоль и поперек него, являются единственными, на которые магнитное поле в приближении холодной плазмы не действует.
Из формулы (22.5) квадрат показателя преломления плазмы для волн, поляризованных вдоль магнитного поля,
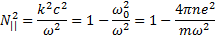 (22.6)
(22.6)
Эту величину можно рассматривать как продольную диэлектрическую проницаемость плазмы. Таков же предельный вид диэлектрической проницаемости любого вещества на больших частотах, который выводится в электродинамике сплошных сред. В отсутствие магнитного поля диэлектрическая проницаемость плазмы изотропна и для любого направления дается выражением (22.6). При наличии магнитного поля поперечная проницаемость отлична отпродольной, как мы уже видели при рассмотрении поляризационного дрейфа.
