Вывод формулы Саха из квазиклассической статистики

Согласно квазиклассической статистике, вероятность нахождения частицы в состоянии с энергией ℰ выражается формулой Больцмана

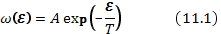
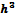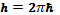где Т — температура в энергетических единицах. Число частиц с энергией ℰ равно вероятности, умноженной на число состояний. Для частицы, не имеющей внутренних степеней свободы, число состояний равно числу элементарных ячеек фазового пространства объемом , где — обычная постоянная Планка. Для электрона с импульсом между 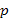и 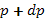фазовый объем

где V — обычный объем. Число электронов в этом объеме

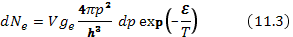
Здесь 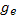— статистический вес, т. е. число состояний с одинаковой энергией, различающихся внутренними степенями свободы. Рассматривая равновесие электронов с атомами, мы можем за нуль энергии считать энергию электрона в атоме. Тогда энергия свободного электрона с импульсом p

где J — энергия ионизации атома (ее часто называют потенциалом ионизации и выражают в электронвольтах). Число свободных электронов на один атом в определенном квантовом состоянии найдется интегрированием по всем значениям импульса

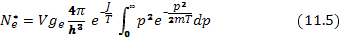
Интеграл берется по формуле

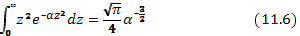
В данном случае 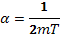,вследствие чего выражение (11.5) дает

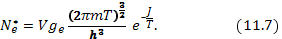
Чтобы получить полное число электронов 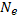, этот результат надо умножить на число атомов в одном квантовом состоянии 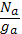, где 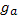— полный статистический вес нейтрального атома. После этого

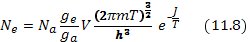
Квазиклассический вывод недостаточно строг, так как приняты два не вполне очевидных допущения. Во-первых, мы считали, что интегрирование выражения (11.3) дает число электронов на один атом в определенном квантовом состоянии. Во-вторых, в равновесии ионизации участвуют также и ионы, и, чтобы учесть это, нужно за V принять объем, приходящийся на один ион в определенном квантовом состоянии:

где 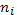— число ионов в единице объема; 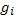— статистический вес иона. Подстановка формулы (11.9) в выражение (11.8) дает формулу Саха в окончательном виде

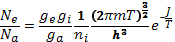
Отношение полных чисел частиц N равно отношению концентраций n, что позволяет записать формулу Саха в симметричном виде

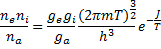
где размерность концентраций в см^-3. Квазиклассический вывод формулы Саха физически нагляден, но содержит допущения, которые строго не обоснованы. Рассмотрение же равновесия ионизации как частного случая химического равновесия позволяет вывести ту же формулу общим методом химической термодинамики без либо нестрогих допущений.

(источник: Д.А. Франк-Каменецкий, Лекции по физике плазмы, гл. 2, §§2-5)

7. Гидродинамическое описание плазмы (МГД-приближение). Магнитная гидродинамика. МГД-уравнения. Вмороженность магнитного поля. Равновесие плазмы. Условия равновесия. Равновесие цилиндрического столба. θ-пинч. Z-пинч.Бессиловые конфигурации. Тороидальная плазма в поле с замкнутными силовыми линиями. Ловушка с гофрированным магнитным полем. Двухжидкостная магнитная гидродинамика. Эффект Холла. Стационарный ток при эффекте Холла. Равновесие плазмы в перекошенном магнитном поле. Диффузия плазмы. Плазма в однородном магнитном поле. Диффузия плазмы в торе. Амбиполярная диффузия слабоионизированной плазмы. Бомовскаядиффузия.

Плазма как сплошная среда

Для приближенного описания плазмы с успехом используются модели, рассматривающие плазму как сплошную среду. Простейшей из них является модель проводящей жидкости. В этой модели свойства плазмы не отличаются от свойств, например, жидкого металла. Наука, изучающая движение проводящих жидкостей или газов посредством совместного решения уравнений гидродинамики и электродинамики, называется магнитной гидродинамикой. Модель проводящей жидкости описывает свойства плазмы в приближении магнитной гидродинамики.

Уравнения движения проводящей среды имеют ту особенность, что в них кроме силы давления входит пондеромоторная сила

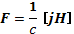(12.1)

гдеj — плотность тока. Если пренебречь вязкостью и другими диссипативными процессами, то уравнение движения плазмы в приближении магнитной гидродинамики будет иметь вид

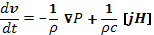(12.2)

Здесь dv/dt —. ускорение рассматриваемого «элемента вещества» или, как говорят в гидродинамике, ускорение «жидкой частицы». В применении к плазме роль жидкой частицы играет совокупность очень большого числа заряженных частиц, но эти частицы выбраны и зафиксированы. Такое рассмотрение движения сплошной среды, когда следят за траекторией выбранного элемента вещества, называется представлением Лагранжа. Ускорение dv/dt есть производная, взятая вдоль траектории данного элемента вещества; ее называют лагранжевой производной или иногда субстанциональной производной, чтобы подчеркнуть, что она относится к выбранному элементу вещества (субстанции). При рассмотрении картины движения сплошной среды в пространстве используется и другое представление, которое называют представлением Эйлера. В этом представлении следят за изменением скорости движения в выбранной точке пространства 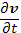или, как ее называют, эйлеровой производной. Хотя эйлерова производная и является производной скорости по времени, она не имеет физического смысла ускорения. Связь между лагранжевой и эйлеровой производными следующая:

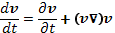
Следовательно, уравнение (12.2) в представлении Эйлера примет вид

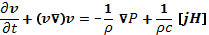(12.2a)

Плотность тока в приближении магнитной гидродинамики находится по закону Ома

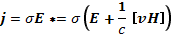(12.3)

гдеЕ — напряженность электрического поля; σ —коэффициент электропроводности, или, иначе, проводимость плазмы; Е* — напряженность электрического поля в системе отсчета, движущейся вместе с плазмой (сопутствующая система). Главный недостаток приближения магнитной гидродинамики в том, что проводимость рассматривается как физическая константа вещества, что в применении к плазме может оказаться весьмадалеким от действительности. Система уравнений (12.2) и (12.3) должна решаться совместно с уравнениями Максвелла. В приближении магнитной гидродинамики рассматриваемые процессы считаются достаточно медленными, чтобы можно было пренебречь током смещения. Тогда из уравнений Максвелла следует, что

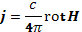(12.4)

Уравнение (12.2) принимает вид

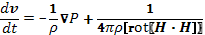(12.5)

Согласно формулам векторного анализа

(12.6)

откуда

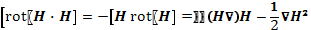(12.7)

Подстановка выражения (12.7) в уравнение (12.5) дает

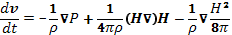(12.8)

Если магнитное поле меняется только поперек своего направления, то второй член правой части обращается в нуль, и уравнение принимает вид

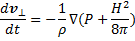(12.9)

где dv_⊥/dt — ускорение поперек магнитного поля. Таким образом, движение плазмы поперек магнитного поля происходит так, как если бы на нее кроме давления Рдействовало еще магнитное давление Н²/8π. Оно имеет в точности ту же величину, что и давление, производимое магнитным полем в пустом пространстве, которое вычисляется в электродинамике. Силу 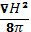в уравнении (12.9) можно с одинаковым правом рассматривать и как пондеромоторную силу взаимодействия магнитного поля с возбужденными им токами, и просто как силу магнитного давления.

Важнейший вывод из модели сплошной среды заключается в том, что на плазму может оказывать воздействие сила магнитного давления. Отсюда вытекает ряд важнейших в научном и практическом отношении следствий: плазму можно удерживать магнитной стенкой, толкать магнитным поршнем; плазменные сгустки можно выстреливать из магнитной пушки.