Движение тел в жидкостях и газах.

При движении симметричных тел в жидкостях и газах возникает сила лобового сопротивления, направленная противоположно скорости движения тела. При ламинарном обтекании шара линии тока расположены симметрично относительно плоскости, проходящей через его центр и перпендикулярной к его скорости. Следовательно, согласно уравнению Бернулли, и давление жидкости будет симметричным относительно этой плоскости, силы давления с обеих сторон шара будут уравновешиваться, и сила сопротивления должна быть равна нулю - парадокс Даламбера. Однако это справедливо лишь при отсутствии сил вязкости в жидкости. При ламинарном обтекании тела жидкостью сила лобового сопротивления полностью зависит от сил вязкости. Стокс, проведя расчеты, получил формулу для силы сопротивления движению шара

F = 6p·h·r·v, (5.13)

где r - радиус шара; v - его скорость; h - коэффициент вязкости.

При возрастании скорости движения тела, начиная с некоторого значения числа Рейнольдса, обтекание тела становится турбулентным, в поверхностном слое поток отрывается от поверхности тела, в результате чего позади тела возникают вихри. Давление в образующейся за телом вихревой области в согласии с уравнением Бернулли оказывается пониженным, поэтому результирующая сила будет отлична от нуля и лобовое сопротивление увеличится.

При обтекании несимметричных тел кроме силы лобового сопротивления возникает подъемная сила. Например, для крыла самолета скорость обтекания его верхней части существенно больше, чем нижней. Согласно уравнению Бернулли давление воздуха в нижней части крыла будет больше, чем сверху. В результате возникает подъемная сила крыла самолета.

ЛЕКЦИЯ 8

Всемирное тяготение.

Законы Кеплера.

К началу 17 столетия большинство ученых окончательно убедилось в справедливости гелиоцентрической системы мира. Однако ученым того времени не были ясны ни законы движения планет, ни причины, определяющие характер их движения.

Иоганн Кеплер (1571-1630) – немецкий астроном, обработав результаты многочисленных наблюдений, проведенных Тихо Браге и им самим, получил законы движения планет вокруг Солнца.

I закон: – Каждая планета движется вокруг Солнца по эллипсу, в одном из фокусов которого находится Солнце. (В 1^ом приближении орбиты можно считать круговыми).

II закон: – Радиус-вектор планеты (т.е. вектор, проведенный от Солнца к планете) за равные промежутки времени описывает равные площади.

III закон: – Квадраты периодов обращения любых двух планет вокруг Солнца относятся как кубы больших полуосей их орбит.

Принимая для простоты, что орбиты являются окружностями (практически это допустимо), ускорение с которым движется планета, можно записать в виде 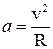, где v – скорость движения планеты, R – радиус орбиты.

Заменив v через 2pR/T (где T – период обращения планеты вокруг Солнца), получим

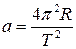(6.1)

Замечание: Равномерное движение тела по окружности характеризуется центростремительным ускорением (точнее нормальной составляющей полного ускорения). Сила, любой природы, вызывающая это ускорение, называется центростремительной. Она приложена к телу, направлена к центру окружности и согласно II закону Ньютона равна 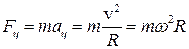. F_ц создается связью, удерживающей тело на окружности.

На основании выражения (6.1) отношение сил, действующих на планеты со стороны Солнца, запишем в виде:

.

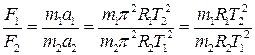Согласно III закону Кеплера: 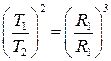. Тогда после подстановки получим: 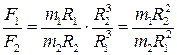или .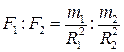

Таким образом, из III закона Кеплера следует, что сила, с которой планета притягивается к Солнцу, пропорциональна массе планеты и обратно пропорциональна квадрату ее расстояния до Солнца, т.е. .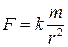

Предположив, что коэффициент пропорциональности k в свою очередь пропорционален массе Солнца M_c, Ньютон пришел к формуле

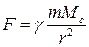– выражающей закон всемирного тяготения.

Впоследствии было обнаружено, что поле тяготения и сила тяготения существуют между любыми телами и тогда закон всемирного тяготения запишется в виде:

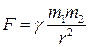(6.2)

ОПРЕДЕЛЕНИЕ: сила, с которой два тела притягивают друг друга, пропорциональна массам этих тел и обратно пропорциональна квадрату расстояния между ними.

g – коэффициент пропорциональности (гравитационная постоянная).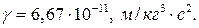

Физический смысл гравитационной постоянной. Если положить m₁, m₂, r равными «1», то сила оказывается численно равна g. Таким образом, два шара с массой 1кг каждый, центры которых отстоят друг от друга на расстоянии 1м, притягиваются взаимно с силой 6,67×10^-11Н.

Закон всемирного тяготения в формулировке (6.2) применим телам, которые можно рассматривать как материальные точки. Для определения силы взаимодействия тел, которые не могут рассматриваться как материальные точки, их нужно разбить на элементарные массы Dm, т.е. небольшие объемы, каждый из которых можно было бы принять за материальную точку.

Проведенные вычисления значения “g” было определено опытным путем измерения силы, с которой притягиваются друг к другу тела известной массы. При таких измерениях возникают большие трудности, т.к. для тел, массы которых могут быть непосредственно измерены, сила притяжения оказывается крайне малой. Так, например, два тела с массой 100 кг каждое, находящиеся на расстоянии 1 м друг от друга, взаимодействуют с силой порядка 10^‑6 Н, т.е. ~10^‑4Г.

Опыт Кавендиша.

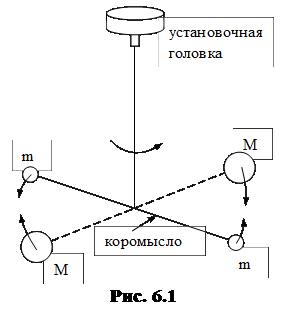Первой успешной попыткой определения «g» были измерения, осуществленные Кавендишем (1798г.), который применил для измерения сил весьма чувствительный метод крутильных весов (рис. 6.1). Два свинцовых шарика m (массой 729г каждый), прикрепленных к концам легкого коромысла, помещались вблизи симметрично расположенных шаров M (с массой по 158кг). Коромысло подвешивалось на упругой нити, по закручиванию которой можно было измерить силу притяжения шаров друг к другу. Верхний коней нити был закреплен в установочной головке, поворотом которой можно было менять расстояние между шарами m и M.

Также следует знать, что II-закон Кеплера является следствием закона сохранения момента импульса. Из рис. 6.2 видно, что описанная радиус-вектором за время dt площадь dS равнаполовине произведения основания треугольникаvdt на высоту треугольника l, котораясовпадает с плечом импульса планеты 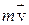по отношению к Солнцу:

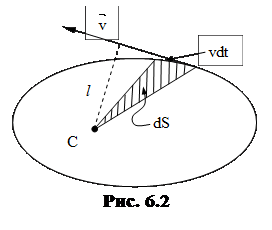
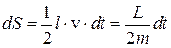
(L – момент импульса планеты, равный m·v·l).

Выражение 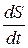называется секториальной скоростью. Таким образом,

.

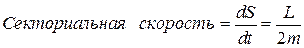Момент импульса в центральном поле сил остается постоянным, следовательно, и секториальная скорость планеты должна быть постоянной. Это означает, что за равные промежутки времени радиус-вектор будет описывать одинаковые площади.