Основные свойства неопределенного интеграла.
Лекция 8. ИНТЕГРИРОВАНИЕ
Неопределенный интеграл
Операция нахождение производной от функции называется дифференцированием. Обратная дифференцированию операция ‒ отыскание функции по ее производной называется интегрированием. Функция F(x), производная которой равна некоторой функции f(x), т.е. F'(x) = f(x), называется первообразной для f(х).
Поскольку производная любой постоянной величины равна нулю, то если первообразная для функции существует, то она не единственна и все они отличаются друг от друга на постоянные величины.
Таким образом, функция f(x) имеет бесконечное множество первообразных вида F(x) + С.
Множество всех первообразных для функции f(x) называется неопределенным интегралом от этой функции и обозначается так: 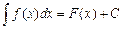 , где
, где 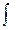 - знак интеграла, f(x) ‒ подынтегральная функция от переменной интегрирования х, f(x)dx ‒ подынтегральное выражение, С ‒ постоянная величина.
- знак интеграла, f(x) ‒ подынтегральная функция от переменной интегрирования х, f(x)dx ‒ подынтегральное выражение, С ‒ постоянная величина.
Часто вместо слов «вычислить неопределенный интеграл» говорят «взять неопределенный интеграл».
Из определения интеграла следует, что:  .
.
Отсюда, по определению дифференциала получаем: 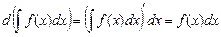 .
.
С другой стороны 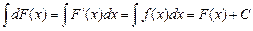 .
.
Эти формулы наглядно иллюстрируют то обстоятельство, что операции дифференцирования и интегрирования взаимно обратимы с точностью до постоянной. В этой связи по аналогии с таблицей формул дифференцирования элементарных функций можно построить таблицу основных интегралов.
Таблица основных интегралов
 |  |
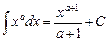 при при 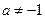 | 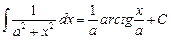 |
 | 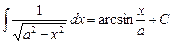 |
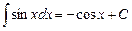 | 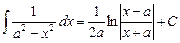 |
 |  |
Справедливость этих формул проверяется непосредственным дифференцированием.
В различных справочниках приводятся обширные таблицы неопределенных интегралов. Но, при решении практических задач, для того, чтобы иметь возможность воспользоваться таблицами, вначале необходимо преобразовать исходный интеграл до вида, который есть в таблице. Для этого надо знать основные свойства неопределенного интеграла и использовать тождественные преобразования подынтегральной функции.
Основные свойства неопределенного интеграла.
1. Постоянный множитель можно выносить за знак неопределенного интеграла:  .
.
2. Неопределенный интеграл от суммы функций равен сумме неопределенных интегралов от этих функций:  .
.
Замечание. Если каждый из суммируемых неопределенных интегралов содержит свою постоянную интегрирования, то для всей суммы записывается одна постоянная интегрирования.
Методы интегрирования
Для вычисления неопределенных интегралов часто используют так называемые стандартные методы интегрирования.
1.Метод интегрирования по частям.
Пусть на некотором промежутке существуют производные функций u = u(х) и v = v(x). По правилу дифференцирования произведения, имеем: d(u·v) = du·v + u·dv. Проинтегрируем это равенство, учитывая, что  ,
, 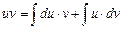 .
.
Получаем: 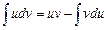 .
.
Эта формула носит название формулы интегрирования по частям. Ее применение полезно в тех случаях, когда подынтегральное выражение можно представить в виде произведения двух функций f(x) = u(x)×v' и выражение vdu = vu'×dx для взятия интеграла проще, чем выражение u× dv = u× v'× dx.
Пример. Найти  .
.
Использование формулы интегрирования по частям позволяет вместо исходного нетабличного интеграла вычислить интеграл от sinx. Покажем это, приведя схему записи удобную при использовании метода интегрирования по частям.
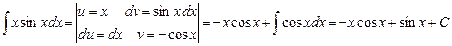
2.Метод замены переменной.
Добиться упрощения подынтегрального выражения можно при помощи метода замены переменной интегрирования. Суть этого метода заключается в замене переменной интегрирования х на некоторую функцию φ(t) с тем, чтобы преобразовать исходный интеграл к более простому виду:
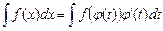 .
.
Эта формула называется формулой замены переменной под знаком неопределенного интеграла.
Алгоритм метода замены переменной следующий. Вначале необходимо найти замену переменной интегрирования х = φ(t), записать интеграл с новой переменной интегрирования t, вычислить его, а затем вновь вернуться к исходной переменной интегрирования.
Пример. Найти 
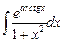 .
.
Решение. Особенностью данного интеграла является то обстоятельство, что его подынтегральное выражение содержит сомножитель 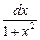 который является дифференциалом функции arctgx.
который является дифференциалом функции arctgx.
Поэтому в данном интеграле целесообразно ввести замену переменной: t = arctg x.
Отсюда 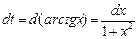 и
и  .
.
Подставляя в исходный интеграл, имеем:
 .
.
Пример. Найти  .
.
Введем замену t = cos x. Тогда dt = -sinx dx, sin3x dx= sin2x sinx dx.
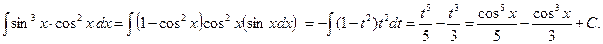
Определенный интеграл
Пусть на отрезке [а, b] задана непрерывная функция f(x). На плоскости XOY, как показано на рисунке график этой функции, отрезок оси абсцисс и прямые х = а и x = b образуют так называемую криволинейную трапецию. Требуется найти площадь такой криволинейной трапеции S.

Разделим отрезок [а,b] на произвольные n частей соответствующими точками с кординатами:
х0 = а < х1 < x2 < ... < хi < xi+1 < ... < xn = b.
Криволинейная трапеция стала состоять из n «узких» криволинейных трапеций (полосок) шириной ∆xi = xi+1 - xi. Каждую i-ю полоску заменим на соответствующий прямоугольник, высота которого равна f(xi), а площадь
Si = f(xi)×∆хi,  .
.
Интуитивно ясно, сумма площадей полученных прямоугольников приближенно равна площади исходной криволинейной трапеции:
 .
.
Будем увеличивать количество разбиений n. При этом каждый раз обязательно должна уменьшатся длина наибольшего из разбиений ∆х, т. е. max ∆х→0 при n→∞. Погрешность такого приближения будет стремиться к нулю, т.е.
 .
.
Для обозначения предельного значения этой суммы Лейбниц ввел символ « 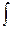 » как стилизацию начертания буквы S ‒ начальной буквы латинского слова Summa.
» как стилизацию начертания буквы S ‒ начальной буквы латинского слова Summa.
К построению сумм рассмотренного вида, которые называют интегральными суммами, приходят при решении многих задач: о массе плоской пластины, о длине дуги кривой линии, о координатах центра тяжести тел, о площади поверхности тел вращения и др.
Если независимо от способа разбиения отрезка [а, b] на части, для функции f(x) существует конечный предел интегральной суммы при n®¥ и max Dxi ® 0, то этот предел называется определенным интегралом функции f(x) от а до b, а сама функция f(x) ‒ интегрируемой на [а, b].
Интеграл от а до b от функции f(x) де икс обозначается следующим образом:
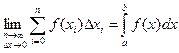 .
.
Числа а и b называются соответственно нижним и верхним пределами интеграла. Если а = b, то положим по определению 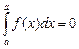 .
.
Сформулируем основные утверждения относительно интегрируемых функций.
Если функция f(x) непрерывна на отрезке [а, b], то она интегрируема на этом отрезке.
Если функция f(x) определена и монотонна на отрезке [а, b], то она интегрируема на этом отрезке.
Если функция f(x) ограничена на отрезке [а, b] и непрерывна во всех точках этого отрезка, кроме конечного числа точек, в которых она имеет разрывы первого рода, то она интегрируема на этом отрезке.
Несобственные интегралы
Для существования определенного интеграла необходимо, чтобы промежуток интегрирования был конечен и непрерывная подынтегральная функция ограничена. Когда не выполняется одно или оба эти условия, приходится прибегать к понятию несобственного интеграла.
Лекция 8. ИНТЕГРИРОВАНИЕ
Неопределенный интеграл
Операция нахождение производной от функции называется дифференцированием. Обратная дифференцированию операция ‒ отыскание функции по ее производной называется интегрированием. Функция F(x), производная которой равна некоторой функции f(x), т.е. F'(x) = f(x), называется первообразной для f(х).
Поскольку производная любой постоянной величины равна нулю, то если первообразная для функции существует, то она не единственна и все они отличаются друг от друга на постоянные величины.
Таким образом, функция f(x) имеет бесконечное множество первообразных вида F(x) + С.
Множество всех первообразных для функции f(x) называется неопределенным интегралом от этой функции и обозначается так: 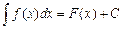 , где
, где 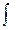 - знак интеграла, f(x) ‒ подынтегральная функция от переменной интегрирования х, f(x)dx ‒ подынтегральное выражение, С ‒ постоянная величина.
- знак интеграла, f(x) ‒ подынтегральная функция от переменной интегрирования х, f(x)dx ‒ подынтегральное выражение, С ‒ постоянная величина.
Часто вместо слов «вычислить неопределенный интеграл» говорят «взять неопределенный интеграл».
Из определения интеграла следует, что:  .
.
Отсюда, по определению дифференциала получаем: 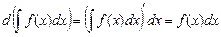 .
.
С другой стороны 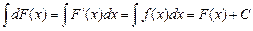 .
.
Эти формулы наглядно иллюстрируют то обстоятельство, что операции дифференцирования и интегрирования взаимно обратимы с точностью до постоянной. В этой связи по аналогии с таблицей формул дифференцирования элементарных функций можно построить таблицу основных интегралов.
Таблица основных интегралов
 |  |
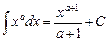 при при 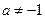 | 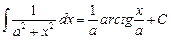 |
 | 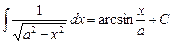 |
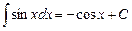 | 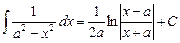 |
 |  |
Справедливость этих формул проверяется непосредственным дифференцированием.
В различных справочниках приводятся обширные таблицы неопределенных интегралов. Но, при решении практических задач, для того, чтобы иметь возможность воспользоваться таблицами, вначале необходимо преобразовать исходный интеграл до вида, который есть в таблице. Для этого надо знать основные свойства неопределенного интеграла и использовать тождественные преобразования подынтегральной функции.
Основные свойства неопределенного интеграла.
1. Постоянный множитель можно выносить за знак неопределенного интеграла:  .
.
2. Неопределенный интеграл от суммы функций равен сумме неопределенных интегралов от этих функций:  .
.
Замечание. Если каждый из суммируемых неопределенных интегралов содержит свою постоянную интегрирования, то для всей суммы записывается одна постоянная интегрирования.
Методы интегрирования
Для вычисления неопределенных интегралов часто используют так называемые стандартные методы интегрирования.
1.Метод интегрирования по частям.
Пусть на некотором промежутке существуют производные функций u = u(х) и v = v(x). По правилу дифференцирования произведения, имеем: d(u·v) = du·v + u·dv. Проинтегрируем это равенство, учитывая, что  ,
, 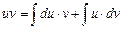 .
.
Получаем: 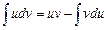 .
.
Эта формула носит название формулы интегрирования по частям. Ее применение полезно в тех случаях, когда подынтегральное выражение можно представить в виде произведения двух функций f(x) = u(x)×v' и выражение vdu = vu'×dx для взятия интеграла проще, чем выражение u× dv = u× v'× dx.
Пример. Найти  .
.
Использование формулы интегрирования по частям позволяет вместо исходного нетабличного интеграла вычислить интеграл от sinx. Покажем это, приведя схему записи удобную при использовании метода интегрирования по частям.
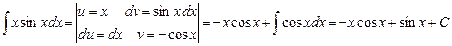
2.Метод замены переменной.
Добиться упрощения подынтегрального выражения можно при помощи метода замены переменной интегрирования. Суть этого метода заключается в замене переменной интегрирования х на некоторую функцию φ(t) с тем, чтобы преобразовать исходный интеграл к более простому виду:
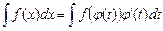 .
.
Эта формула называется формулой замены переменной под знаком неопределенного интеграла.
Алгоритм метода замены переменной следующий. Вначале необходимо найти замену переменной интегрирования х = φ(t), записать интеграл с новой переменной интегрирования t, вычислить его, а затем вновь вернуться к исходной переменной интегрирования.
Пример. Найти 
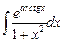 .
.
Решение. Особенностью данного интеграла является то обстоятельство, что его подынтегральное выражение содержит сомножитель 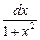 который является дифференциалом функции arctgx.
который является дифференциалом функции arctgx.
Поэтому в данном интеграле целесообразно ввести замену переменной: t = arctg x.
Отсюда 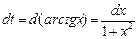 и
и  .
.
Подставляя в исходный интеграл, имеем:
 .
.
Пример. Найти  .
.
Введем замену t = cos x. Тогда dt = -sinx dx, sin3x dx= sin2x sinx dx.
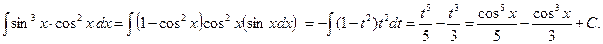
Определенный интеграл
Пусть на отрезке [а, b] задана непрерывная функция f(x). На плоскости XOY, как показано на рисунке график этой функции, отрезок оси абсцисс и прямые х = а и x = b образуют так называемую криволинейную трапецию. Требуется найти площадь такой криволинейной трапеции S.

Разделим отрезок [а,b] на произвольные n частей соответствующими точками с кординатами:
х0 = а < х1 < x2 < ... < хi < xi+1 < ... < xn = b.
Криволинейная трапеция стала состоять из n «узких» криволинейных трапеций (полосок) шириной ∆xi = xi+1 - xi. Каждую i-ю полоску заменим на соответствующий прямоугольник, высота которого равна f(xi), а площадь
Si = f(xi)×∆хi, 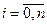 .
.
Интуитивно ясно, сумма площадей полученных прямоугольников приближенно равна площади исходной криволинейной трапеции:
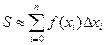 .
.
Будем увеличивать количество разбиений n. При этом каждый раз обязательно должна уменьшатся длина наибольшего из разбиений ∆х, т. е. max ∆х→0 при n→∞. Погрешность такого приближения будет стремиться к нулю, т.е.
 .
.
Для обозначения предельного значения этой суммы Лейбниц ввел символ « 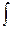 » как стилизацию начертания буквы S ‒ начальной буквы латинского слова Summa.
» как стилизацию начертания буквы S ‒ начальной буквы латинского слова Summa.
К построению сумм рассмотренного вида, которые называют интегральными суммами, приходят при решении многих задач: о массе плоской пластины, о длине дуги кривой линии, о координатах центра тяжести тел, о площади поверхности тел вращения и др.
Если независимо от способа разбиения отрезка [а, b] на части, для функции f(x) существует конечный предел интегральной суммы при n®¥ и max Dxi ® 0, то этот предел называется определенным интегралом функции f(x) от а до b, а сама функция f(x) ‒ интегрируемой на [а, b].
Интеграл от а до b от функции f(x) де икс обозначается следующим образом:
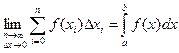 .
.
Числа а и b называются соответственно нижним и верхним пределами интеграла. Если а = b, то положим по определению 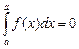 .
.
Сформулируем основные утверждения относительно интегрируемых функций.
Если функция f(x) непрерывна на отрезке [а, b], то она интегрируема на этом отрезке.
Если функция f(x) определена и монотонна на отрезке [а, b], то она интегрируема на этом отрезке.
Если функция f(x) ограничена на отрезке [а, b] и непрерывна во всех точках этого отрезка, кроме конечного числа точек, в которых она имеет разрывы первого рода, то она интегрируема на этом отрезке.
