Классификация механического движения по ускорению.

Отличить характер одного движения от другого можно по многим параметрам: по виду траектории, характеру изменения скорости и т д. Наиболее общим (в информативном смысле) считается классификация по ускорению. Ускорение непосредственно связано с причиной изменения состояния движения –силой. Пусть вектор скорости меняется с течением времени и по величине и по направлению.

По определению: 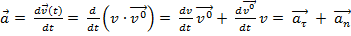. Здесь 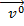- единичный вектор направления ).

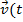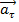– тангенциальное ускорение, характеризует изменение вектора 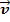только по величине.

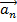– нормальное ускорение, характеризует изменение вектора 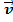только по направлению.

1. 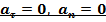, вектор скорости не изменяется ни по величине 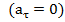, ни по направлению ( 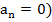, это – равномерное, прямолинейное движение. Найдём параметры и закон движения.

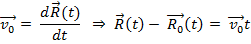
Закон движения: 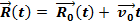. –в векторной системе отсчёта.

В декартовой системе координат: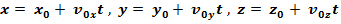

2. 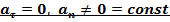Это означает, что модуль вектора скорости не меняется, в то время как за любые равные промежутки времениего направление меняется на равные углы

Это- равномерное движение по окружности. Найдём параметры и закон движения.

=

.

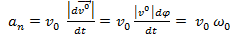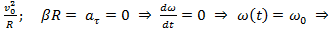
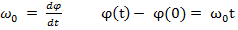Закон движения: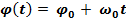

3. 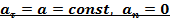равнопеременное, прямолинейное движение ( );

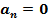(равноускоренное 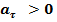или равнозамедленное )

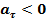Так как вектор скорости не меняется по направлению ( 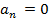), то пусть движение происходит по направлению оси OX. Найдём параметры и закон движения.

Закон

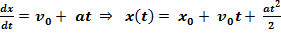движения

В общем случае: 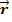= 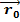+ 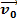t + ;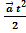

4. 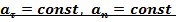–равнопеременное ( 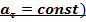движение по окружности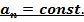

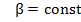Угловое ускорение в силу 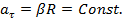Найдём параметры и закон движения в угловых переменных.

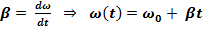Угловая скорость и закон

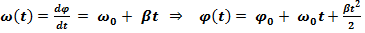движения

5. Колебательное, - движение, при котором координаты точки повторяются через равные промежутки времени (периоды). Простейшими периодическими функциями являются гармонические функции времени - синус или косинус. При этом как первая, так и вторая их производные будут также гармоническими функциями. Поэтому легко «угадать» вид ускорения при гармонических колебаниях материальной точки:

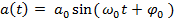
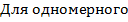случая 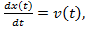легко найти закон изменения координаты:

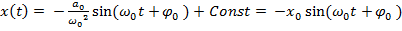+ Const.

Постоянные интегрирования, начальная фаза 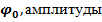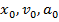, находятся из начальных условий при решении динамических дифференциальных уравнений колебаний. Циклическая частота 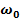(число полных колебаний за 2 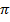секунд) зависит от колебательных свойств системы.

Итак, закон гармонического колебания: 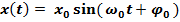.Учитывая, что =

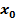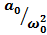
получим: 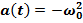x(t). Ускорение материальной точки, совершающей гармоническое колебательное движение, пропорционально смещению от положения равновесия и направлено в сторону точки равновесия.

6. Волновое движение

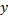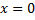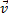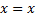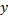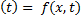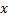Процесс распространения колебаний в пространстве

с течением времени – волновой процесс или волна.

Механичекие волны могут распространяться в упругой

среде. Простейшая модель упругой среды – материальные

точки, между которыми десйствуют упругие силы.

В плоской волне каждая мат.точка имеет координаты x,y. Пусть точка с координатой x=0 совершает кобание вдоль оси OY по закону: ,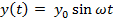

Полагаем далее, что затухания нет, следовательно амплитуда колебаний для всех точек по оси OX

одинакова: 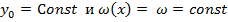. Смещение точек по оси OX не происходит (поперечная волна) Смещение первой точки нарушает равновесие второй точки и т.д.

Вдоль оси OX начнётся распространяться процесс колебаний c некоторой скоростью 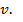Заметим, что все частицы начинают движение от положения равновесия так же, как и первая, но с запаздыванием по времени на 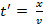. Тогда время начала колебаний произвольной точки вдоль оси OX будет функцией координаты. Можно сформулировать словесное описание такого процесса как: кая точка среды начинает своё колебательное движение как начинала его первая 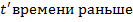. Соответственно математическая запись закона распространения колебаний 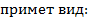y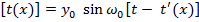

Итак, закон волнового движения, уравнение волны: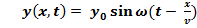

Важнейшим параметром волнового процесса является длина волны 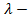это расстояние, на которое распространится волна за время, равное периоду колебания Т, то есть .Поскольку период связан с линейной частотой ( числом колебаний за 1 секунду) 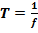,то .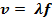

Заметим, что когда через время t=T первая точка x=0 начнёт своё второе колебание, другая точка с координатой x= 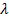начнёт своё, точно такое же движение, первый раз. Через некоторое время на оси

уже будет множество точек, которые имеют одинаковые значения 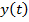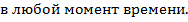Говорят, что они колеблются в одинаковой фазе. Не трудно понять, что любые две точки волны, отстоящие друг от друга на расстояние 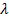, будут обладать таким свойством. Тогда: кратчайшее расстояние между точками, колеблющимися в одинаковой фазе – длина волны.

Волновое число можно связать с длинной волны: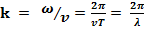

Кинематические уравнения по видам движения: координата, скорость, ускорение:

1.Уравнение поступательного движения: ;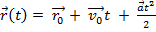

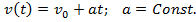
2.Уравнение вращательного движения: ; + ;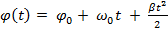

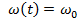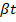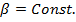
3.Уравнение колебательного движения: 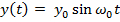; v(t) = .

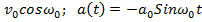Здесь 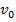= 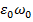; ; 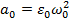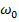- зависит от колебательных (упругих) свойств системы.

4.Уравнение волнового движения: 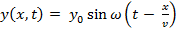; скорость волны 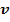зависит от упругих свойств среды.

Практические задачи.

Задача 1.

Скорость материальной точки задана уравнениями: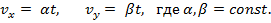

Найти кинематическое уравнение движения и траекторию.

1) Запишем условие в векторной форме: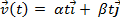

2) Ускорение: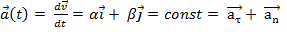

3) 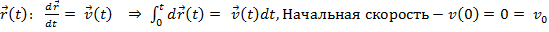по условию задачи.

4) Выберем начальное положение точки: .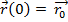

Запишем кинематическое уравнение движения: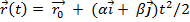

В координатной форме:

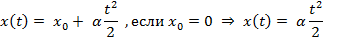
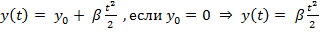
Для получения уравнения траектории необходимо исключить время :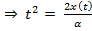

Тогда уравнение траектории: 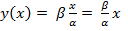- прямая линия.

Задача 2.

Материальная точка движется со скоростью 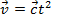Найти уравнение движения.

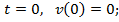
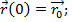
Начальные условия: 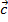-постоянный вектор

Решение. 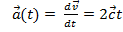; 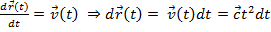Интегрируя , получим:

.

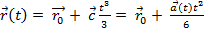Движение твердого тела

Твердое тело – это совокупность материальных точек, расстояние между которыми в процессе движения остается неизменным.

Степень свободы твердого тела– число независимых переменных, описывающих состояние данной системы.

Для того чтобы “найти” твердое тело в Декартовой системе координат необходимо знать координаты трех его точек, не лежащих на одной прямой. Так как каждая точка имеет три координаты, то 9 координат достаточно, чтобы определить положение твёрдого тела в пространстве. Однако число координат (степеней свободы) можно сократить, используя свойство неизменности расстояний между выбранными точками. Т.о – число степеней свободы твёрдого тела в трёхмерном пространстве может сведено к 6 (шести).

Поступательным движением твердого теланазовем движение, при котором векторы перемещения материальных точек тела одинаковы за любой промежуток времени. Или любая прямая, проведенная в теле остается параллельна самой себе.

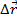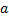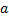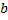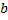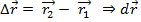
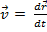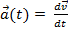; - одинаковы для всех точек тела.

При поступательном движении достаточно знать закон движения одной точки твердого тела.

Вращательное движение.При вращении вокруг неподвижной оси радиус-векторы точек твердого тела, относительно точек отсчета, взятых на оси за любые равные промежутки времени совершают повороты на равные углы.

Если взять в качестве координат угол поворота 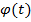, то любые точки будут иметь равные угловые скорости 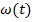и угловые ускорения .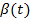