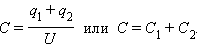Электрическая емкость уединенного проводника
Уединенным называется проводник, вблизи которого нет других заряженных тел, диэлектриков, которые могли бы повлиять на распределение зарядов данного проводника.
Отношение величины заряда к потенциалу для конкретного проводника есть величина постоянная, называемая электроемкостью (емкостью) С ,  .
.
Таким образом,электроемкость уединенного проводника численно равна заряду, который необходимо сообщить проводнику, чтобы изменить его потенциал на единицу. Опыт показал, что электроемкость уединенного проводника зависит от его геометрических размеров, формы, диэлектрических свойств окружающей среды и не зависит от величины заряда проводника.
Рассмотрим уединенный шар радиуса R, находящийся в однородной среде с диэлектрической проницаемостью e. Ранее было получено, что потенциал шара равен  . Тогда емкость шара
. Тогда емкость шара 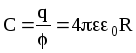 , т.е. зависит только от его радиуса.
, т.е. зависит только от его радиуса.
За единицу емкости принимается 1фарад (Ф). 1Ф - емкость такого уединенного проводника, потенциал которого изменится на 1В при сообщении заряда 1Кл. Фарад - очень большая величина, поэтому на практике используют дольные единицы : миллифарад (мФ, 1мФ=10-3Ф), микрофарад (мкФ, 1мкФ=10-6Ф), нанофарад (нФ, 1нФ=10-9Ф), пикофарад (пФ, 1пФ=10-12Ф).
Уединенные проводники даже очень больших размеров обладают малыми емкостями. Емкостью в 1Ф обладал бы уединенный шар радиуса, в 1500 раз большего радиуса Земли. Электроемкость Земли составляет 0.7 мФ

Ёмкость цилиндрического конденсатора — характеристика плоского конденсатора, мера его способности накапливать электрический заряд.
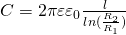
Для определения емкости цилиндрического конденсатора, который состоит из двух полых коаксиальных цилиндров с радиусами r1 и r2 (r2 > r1), один вставлен в другой, считаем поле радиально-симметричным и действующим только между цилиндрическими обкладками, так же пренебрегаем краевыми эффектами. Разность потенциалов между обкладками считаем по формуле для разности потенциалов поля равномерно заряженного бесконечного цилиндра с линейной плотностью τ =Q/l. При наличии диэлектрика между обкладками разность потенциалов

Подставим в формулу электроемкости конденсатора и у нас получится формула для цилиндрического конденсатора:
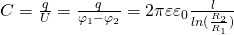
Электроемкость сферического конденсатора — характеристика плоского конденсатора, мера его способности накапливать электрический заряд.

Чтобы найти емкость сферического конденсатора, который состоит из двух концентрических обкладок, разделенных сферическим слоем диэлектрика, используем формулу для разности потенциалов между двумя точками, лежащими на расстояниях r1 и r2 (r2 > r1) от центра заряженной сферической поверхности. При наличии диэлектрика между обкладками разность потенциалов будет выглядеть так:
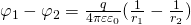
Подставим данное выражение в формулу электроемкости конденсатора и получим емкость конденсатора для сферического тела:

При малой величине зазора, то есть  , а следовательно можно считать, что
, а следовательно можно считать, что 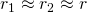 емкость сферического конденсатора будет равна
емкость сферического конденсатора будет равна  . Площадь сферы
. Площадь сферы 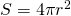 следовательно формула будет совпадать с формулой емкости плоского конденсатора
следовательно формула будет совпадать с формулой емкости плоского конденсатора 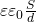
1  . Рассмотрим систему, состоящую из двух проводников, заряды которых численно равны, но противоположны по знаку. Обозначим разность потенциалов проводниковj1-j2 а абсолютное значениеих зарядов q. Если проводники находятся вдали от каких бы то ни было заряженных тел и иных проводников, то, как показывают и теория и эксперименты, разность потенциалов j1-j2 пропорциональна заряду q, т. е. j1-j2=q/C. Скалярная величина С, равная абсолютному значению отношения электрического заряда одного проводника к разности электрических потенциалов двух проводников при условии, что эти проводники имеют одинаковые по модулю, но противоположные по знаку заряды и что все другие проводники бесконечно удалены, называетсявзаимной электрической емкостью двух проводников (электрической емкостью между двумя проводниками):
. Рассмотрим систему, состоящую из двух проводников, заряды которых численно равны, но противоположны по знаку. Обозначим разность потенциалов проводниковj1-j2 а абсолютное значениеих зарядов q. Если проводники находятся вдали от каких бы то ни было заряженных тел и иных проводников, то, как показывают и теория и эксперименты, разность потенциалов j1-j2 пропорциональна заряду q, т. е. j1-j2=q/C. Скалярная величина С, равная абсолютному значению отношения электрического заряда одного проводника к разности электрических потенциалов двух проводников при условии, что эти проводники имеют одинаковые по модулю, но противоположные по знаку заряды и что все другие проводники бесконечно удалены, называетсявзаимной электрической емкостью двух проводников (электрической емкостью между двумя проводниками):
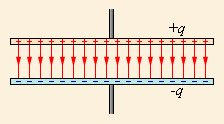
Простейший конденсатор – система из двух плоских проводящих пластин, расположенных параллельно друг другу на малом по сравнению с размерами пластин расстоянии и разделенных слоем диэлектрика. Такой конденсатор называется плоским. Электрическое поле плоского конденсатора в основном локализовано между пластинами (рис. 1.6.1); однако, вблизи краев пластин и в окружающем пространстве также возникает сравнительно слабое электрическое поле, которое называют полем рассеяния. В целом ряде задач приближенно можно пренебрегать полем рассеяния и полагать, что электрическое поле плоского конденсатора целиком сосредоточено между его обкладками (рис. 1.6.2). Но в других задачах пренебрежение полем рассеяния может привести к грубым ошибкам, так как при этом нарушается потенциальный характер электрического поля (см. § 1.4).
 |
| Рисунок 1.6.1. Поле плоского конденсатора |
 |
| Рисунок 1.6.2. Идеализированное представление поля плоского конденсатора. Такое поле не обладает свойством потенциальности |
Каждая из заряженных пластин плоского конденсатора создает вблизи поверхности электрическое поле, модуль напряженности которого выражается соотношением
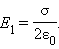 |
Согласно принципу суперпозиции, напряженность 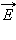 поля, создаваемого обеими пластинами, равна сумме напряженностей
поля, создаваемого обеими пластинами, равна сумме напряженностей  и
и  полей каждой из пластин:
полей каждой из пластин:
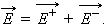 |
Внутри конденсатора вектора  и
и  параллельны; поэтому модуль напряженности суммарного поля равен
параллельны; поэтому модуль напряженности суммарного поля равен
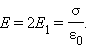 |
Вне пластин вектора  и
и  направлены в разные стороны, и поэтому E = 0. Поверхностная плотность σ заряда пластин равна q / S, где q – заряд, а S – площадь каждой пластины. Разность потенциалов Δφ между пластинами в однородном электрическом поле равна Ed, где d – расстояние между пластинами. Из этих соотношений можно получить формулу для электроемкости плоского конденсатора:
направлены в разные стороны, и поэтому E = 0. Поверхностная плотность σ заряда пластин равна q / S, где q – заряд, а S – площадь каждой пластины. Разность потенциалов Δφ между пластинами в однородном электрическом поле равна Ed, где d – расстояние между пластинами. Из этих соотношений можно получить формулу для электроемкости плоского конденсатора:
|
Таким образом, электроемкость плоского конденсатора прямо пропорциональна площади пластин (обкладок) и обратно пропорциональна расстоянию между ними. Если пространство между обкладками заполнено диэлектриком, электроемкость конденсатора увеличивается в ε раз:
|
Сферический и цилиндрический конденсатор.
Примерами конденсаторов с другой конфигурацией обкладок могут служить сферический и цилиндрический конденсаторы.Сферический конденсатор – это система из двух концентрических проводящих сфер радиусов R1 и R2. Цилиндрический конденсатор – система из двух соосных проводящих цилиндров радиусов R1 и R2 и длины L. Емкости этих конденсаторов, заполненных диэлектриком с диэлектрической проницаемостью ε, выражаются формулами:
|
Параллельное и последовательное соединение конденсаторов.
Конденсаторы могут соединяться между собой, образуя батареи конденсаторов. При параллельном соединении конденсаторов (рис. 1.6.3) напряжения на конденсаторах одинаковы: U1 = U2 = U, а заряды равны q1 = С1U и q2 = C2U. Такую систему можно рассматривать как единый конденсатор электроемкости C, заряженный зарядом q = q1 + q2 при напряжении между обкладками равном U. Отсюда следует
|


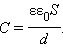
 (сферический конденсатор),
(сферический конденсатор), 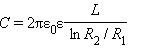 (цилиндрический конденсатор).
(цилиндрический конденсатор).