Поле, образованное двумя разноименными заряженными плоскостями (бесконечно большими)

Поле двух параллельных бесконечно больших плоскостей, заряженных разноименно с одинаковой по величине постоянной поверхностной плотностью 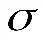можно рассматривать как суперпозицию полей, создаваемых каждой из плоскостей в отдельности. В области между плоскостями (рис.2.13) складываемые поля имеют одинаковое направление, так что результирующая напряженность равна

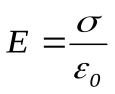
(4)

В не объема, ограниченного плоскостями, складываемые поля имеют противоположные направления, так что результирующая напряженность равна нулюE=0. Таким образом, поле сосредоточено между плоскостями. Напряженность поля во всех точках этой области одинакова по величине и по направлению. Поле, обладающее такими свойствами, называетсяоднородным. Линии напряженности однородного поля представляют собой совокупность параллельных равноотстоящих прямых.

Полученный результат приблизительно справедлив и в случае плоскостей конечных размеров, если расстояние между плоскостями значительно меньше их линейных размеров (плоский конденсатор). В этом случае заметные отклонения поля от однородности напряженности наблюдаются только вблизи краев пластин (рис. 2.14).

Пусть две бесконечные плоскости заряжены разноименными зарядами с одинаковой по величине плотностью σ .

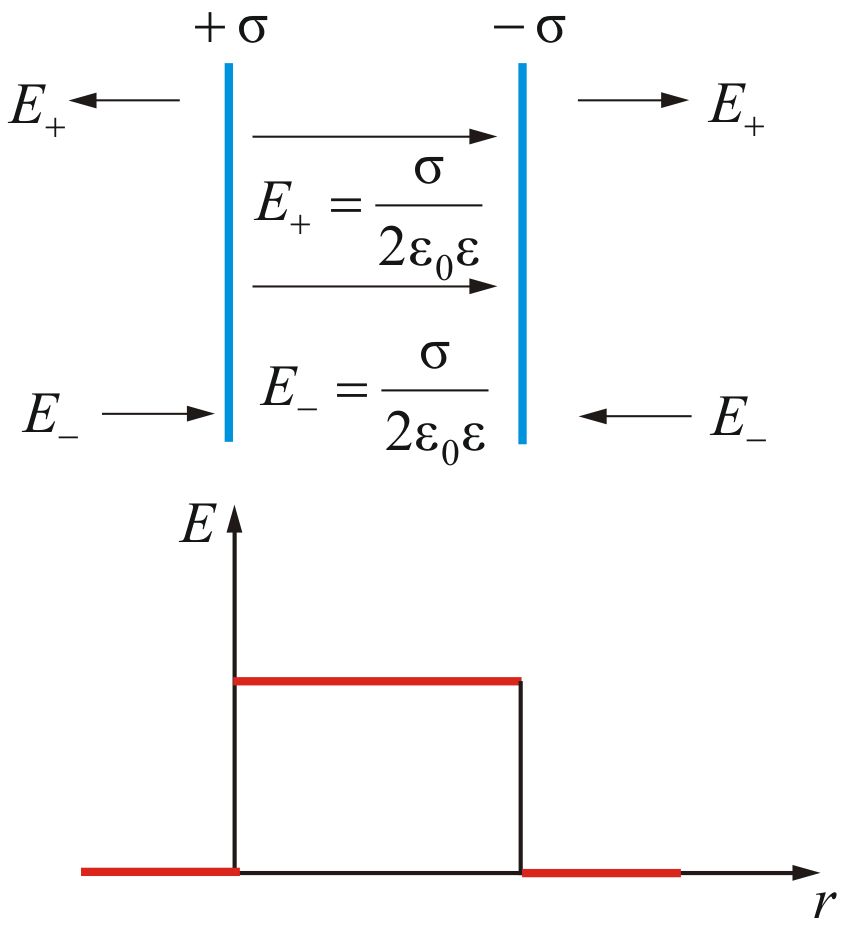
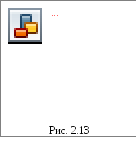
Результирующее поле, как было сказано выше, находится как суперпозиция полей, создаваемых каждой из плоскостей. Тогда внутри плоскостей

Вне плоскостейнапряженность поля .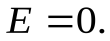

Распределение напряженности электростатического поля между пластинами конденсатора показано на рисунке .

Между пластинами конденсатора действует сила взаимного притяжения (на единицу площади пластин):

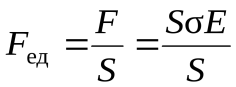, т.е. .

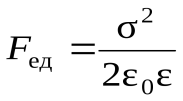Механические силы, действующие между заряженными телами, называют пондермоторными.

Тогда сила притяжения между пластинами конденсатора:

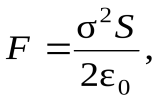
где S– площадь обкладок конденсатора. Т.к. 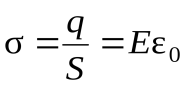, то

.

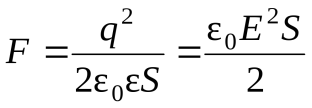Это формула для расчета пондермоторной силы.

· Поле бесконечной заряженной нити

Рассмотрим поле, созданное зарядом, равномерно распределенным по бесконечной нити. Эту задачу мы решили на прошлой лекции, воспользовавшись принципом суперпозиции электрических полей (см. 1.11).

Теперь покажем, несколько проще можно рассчитать это поле с помощью теоремы Гаусса.

Определим напряжённость поля на расстоянии r от нити, заряженной с постоянной линейной плотностью :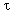

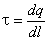, [Кл/м] (2.10)

Окружим нить замкнутой цилиндрической поверхностью (рис. 2.7.). Высота цилиндра — h, а радиус его основания — r.

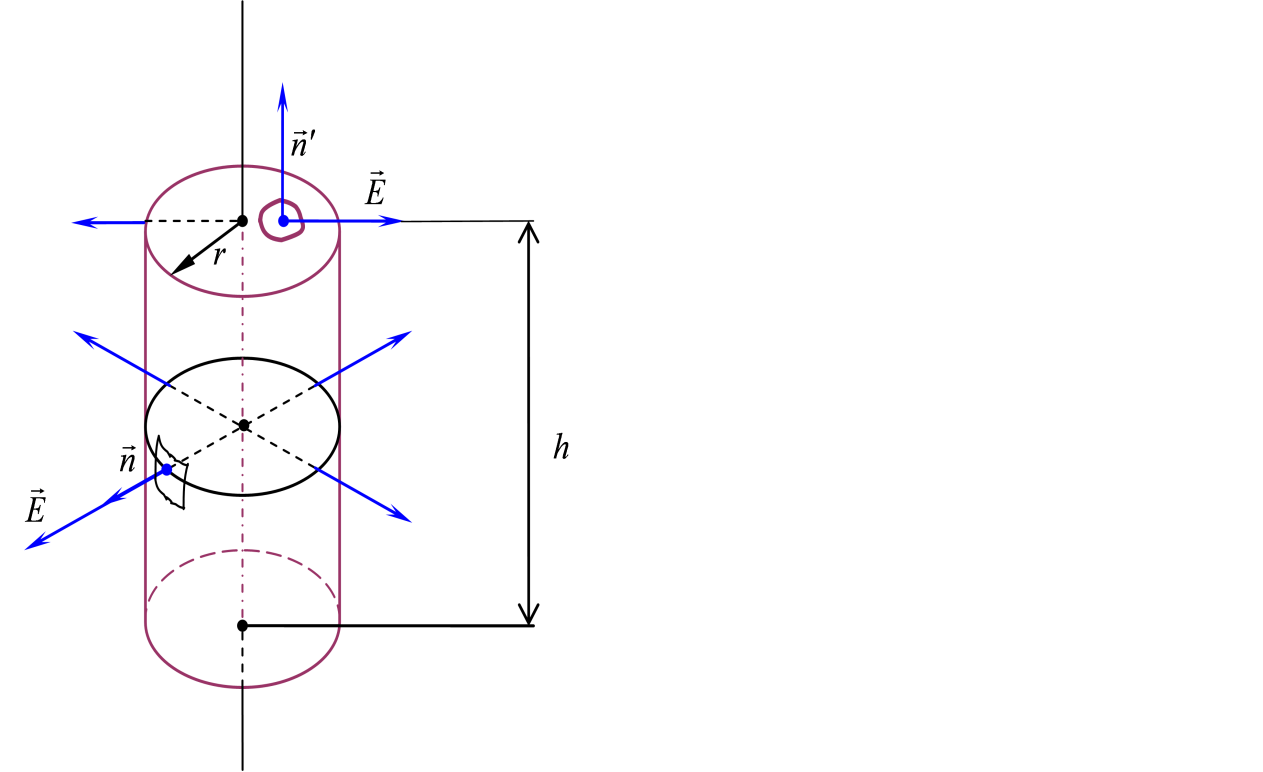
Рис. 2.7.

Поле, созданное заряженной нитью, обладает цилиндрической симметрией. В связи с этим векторы напряжённости во всех точках боковой поверхности цилиндра будут одинаковы по модулю и направлены радиально, то есть перпендикулярно к боковой поверхности цилиндра. На основаниях цилиндра векторы 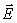, направленные по-прежнему радиально, «скользят» по основанию, образуя прямой угол с нормалью .

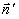Вычислим поток вектора 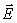через поверхность выбранного цилиндра. Полный поток через эту замкнутую «гауссову» поверхность складывается из потока через боковую поверхность цилиндра и через два его основания:

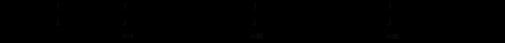
Последние два интеграла равны нулю, так как «скользящие» по основаниям цилиндра векторы 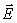не пронизывают их и не создают никакого потока. Формально эти два интеграла равны нулю, так как между векторам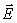и и 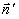прямой угол и 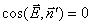. Таким образом

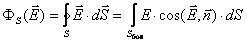
Во всех точках боковой поверхности цилиндра E =Е_r = const и .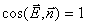

Поэтому поток через боковую поверхность цилиндра равен

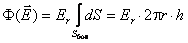(2.11)

Это поток вектора напряжённости электрического поля, вычисленный по определению потока.

Теперь воспользуемся теоремой Гаусса, отметив предварительно, что «заряд, заключённый внутри гауссовой поверхности» в данном случае сосредоточен на отрезке нити h — на оси цилиндра:

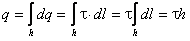
Таким образом

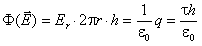(2.12)

Отсюда теперь легко получить знакомую нам гиперболическую зависимость напряжённости поля от расстояния до нити — r (см. 1.11).