Условие независимости от пути интегрирования

Обычно криволинейный интеграл зависит от линии интегрирования. Взятый вдоль разных линий, соединяющих точки А и В, он будет иметь различные значения. Но если в некоторой односвязной области D выражение Pdx + Qdy является полным дифференциалом, то криволинейный интеграл 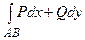не зависит от линии интегрирования, соединяющей точки А и В, а взятый по любой замкнутой линии, равен нулю, т.е. 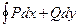= 0.

Напомним, что выражение Pdx + Qdy будет полным дифференциалом некоторой функции u(x, y), если 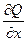= 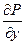и P, Q, P’_y, Q’_x непрерывны в области D. Тогда интеграл можно вычислить по формуле Ньютона-Лейбница,

.

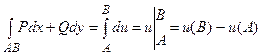Пример 2.1. Теплота сгорания топлива q (МДж/кг), КПД двигателей h(%). Рассматривая летательный аппарат как материальную точку массы m, найти массу горючего M, необходимого для перемещения аппарата в силовом поле

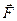(x, y) =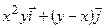

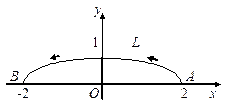вдоль траектории L:

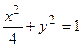
Рис.2.3

от точки A(2; 0) до точки B(-2; 0)(сила 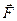дана в килоньютонах, координаты - в километрах).

Решение. Найдем работу, совершаемую переменной силой 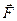при движении материальной точки единичной массы вдоль траектории L по формуле (2.2). Для этого зададим дугу L параметрически: 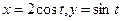; в точке А значение параметра t = 0, в точке В - t = p.

=

=

= .

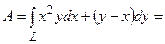
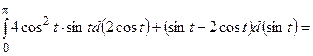
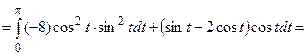
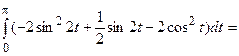
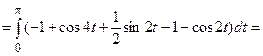
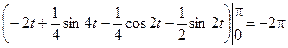Так как сила дана в кН = 10³Н, а путь в км = 10³м, то работа имеет размерность 10⁶Дж=МДж. Работа А отрицательна потому, что для перемещения тела вдоль траектории L от точки А до точки В необходимо совершить работу против силы .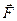

По определению КПД есть отношение полезной энергии Е_полезн к затраченной Е_затр, т.е. 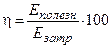(%). Будем считать, что полезная энергия равна по модулю совершенной работе. Отсюда

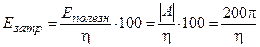(МДж).

Вычисленная энергия необходима для перемещения точки единичной массы, следовательно, чтобы переместить вдоль пути L летательный аппарат массы m, необходимо затратить энергию в m раз больше, т.е.

Е = mЕ_затр = 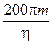(МДж).

Расход горючего при этом 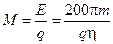(кг).

Ответ: масса горючего 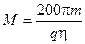кг.

Пример 2.2.Вычислить криволинейный интеграл по замкнутому контуру 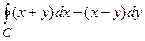, где С – эллипс с полуосями а и b.

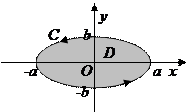Решение. В данном случае P = x + y, Q = -(x – y). Частные производные 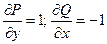. Условие непрерывности функций P и Q и их частных производных выполняется, контур замкнут, поэтому можно применить формулу Грина (2.3).

.

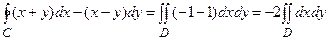Последний интеграл равен площади области D, т.е. площади эллипса: .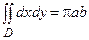

Ответ: - 2π ab.

ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ

ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ

ПЕРВОГО РОДА

Рис. 3.1

Пусть заданы некоторая непрерывная функция F(x, y, z) и гладкая поверхность S, определяемая явным уравнением z = f(x, y), пусть область D - проекция поверхности S в плоскости хОу (рис. 3.1). Разобьем произвольным образом поверхность S на n элементов и обозначим i-ый элемент - Ds_i, в каждом из них выберем произвольную точку M_i. Составим сумму

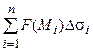. (3.1)

Определение. Поверхностным интегралом первого рода называется предел интегральных сумм (3.1) при стремлении максимального диаметра площадок Ds_i к нулю, т.е.

.

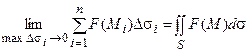Поверхностный интеграл первого рода называют также поверхностным интегралом от скалярной функции.