Физический смысл криволинейного интеграла I рода

Криволинейный интеграл от функции r(x, y, z) по кривой АВ равен массе материальной кривой АВ, имеющей переменную линейную плотность r(x, y, z), т.е.

.

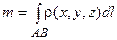Если r= 1, то интеграл равен длине дуги кривой АВ,

.

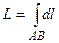Вычисление криволинейного интеграла I рода

1. Если плоская кривая задана уравнением y = y(x), где a £ x £ b, то элемент дуги равен 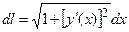, тогда криволинейный интеграл вычисляется по формуле

.

2. Если плоская кривая задана параметрически х=х(t), y=y(t) (t₁ £ t £ t₂), то

, .

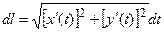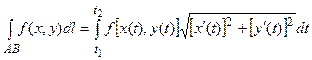3. Если кривая пространственная, тогда

.

КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ

ВТОРОГО РОДА

Пусть в пространстве заданы: направленная гладкая кривая АВ, функция P(x, y, z) на этой кривой, {l_i} - произвольное разбиение кривой АВ, точка M_iÎl_i, Dx_i - проекция дуги l_i на ось Ох.

Определение. Предел интегральных сумм

,

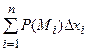если максимальный диаметр разбиения {l_i} стремится к нулю, называется криволинейным интегралом второго рода по координате x и обозначается

.

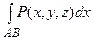Аналогично определяются криволинейные интегралы по координатам у и z, их обозначают

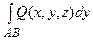и .

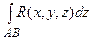Определение. Интеграл

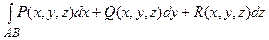
называется общим криволинейным интегралом второго рода или криволинейным интегралом по координатам.

Отметим, что при изменении направления кривой АВ криволинейный интеграл второго рода меняет свое значение на противоположное, т.е.

= .

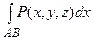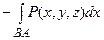Механический смысл криволинейного интеграла

Предположим, что при движении по кривой АВ материальная точка Р, имеющая единичную массу, переходит из положения А в положение В. Дифференциал радиус-вектора точки кривой направлен по касательной и вычисляется по формуле:

.

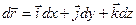Во время движения на точку действует переменная сила , заданная своими проекциями F_x, F_y, F_z на координатные оси, т.е.

.

Тогда работа силы 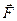на малом участке ∆l_i равна скалярному произведению 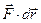, а на всем пути АВ равна общему криволинейному интегралу второго рода

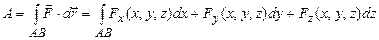(2.2)

Поэтому криволинейный интеграл второго рода называют также криволинейным интегралом от векторной функции.

Вычисление криволинейного интеграла II рода

1. Если пространственная кривая задана параметрическими уравнениями х = х(t), y=y(t), z = z(t) (t₁ £ t £ t₂), то вместо каждой координаты в интеграл надо подставить ее выражение

=

=

.

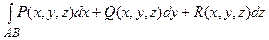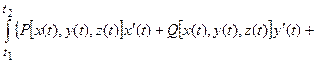
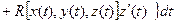2. Если кривая плоская и задана уравнением y=j(x), где a £ x £ b, то

.

3. Если плоская кривая интегрирования замкнута, то криволинейный интеграл обозначают 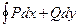. Интеграл не зависит от того, какую точку берут за начало. Положительным направлением обхода считают движение по часовой стрелке. При вычислении интеграла по замкнутому контуру можно использовать формулу Грина, которая позволяет перейти к двойному интегралу.

Формула Грина

Если C – граница области D и функции P и Q вместе со своими частными производным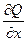и и 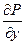непрерывны в области D, то справедлива формула Грина:

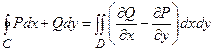, (2.3)

контур обходится так, чтобы область оставалась слева (пример 2.2).