Приложения двойного интеграла

1. Площадь поверхности

Пусть поверхность σзадана уравнением z = f(x, y), где f(x, y) имеет непрерывные частные производные первого порядка в некоторой замкнутой ограниченной области D плоскости хОу. Площадь поверхности σвычисляется по формуле

S =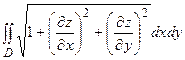

Если уравнение поверхности задано в виде х = ψ(y, z) или у = η (х, z), то площадь вычисляется по формулам:

S = ,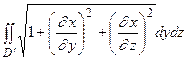

S = ,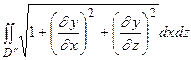

где D’ и D’’ - проекции на плоскостях yOz и xOz данной поверхности.

2. Масса пластины

Если пластина занимает на плоскости хОу область D и имеет переменную поверхностную плотность γ = γ(х, у), то масса m пластины выражается двойным интегралом

.

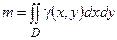3. Статические моменты

Статические моменты пластины относительно осей Ох и Оу вычисляются по формулам:

, .

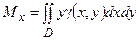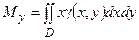4. Координаты центра тяжести

Координаты центра тяжести пластины, имеющей плотность γ = γ(х, у), вычисляются по формулам:

, ,

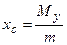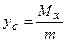где m - масса пластины, М_х, М_y - ее статические моменты.

Если пластина однородная, т.е. γ = const, то эти формулы принимают вид

, ,

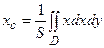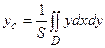где S - площадь пластины.

5. Моменты инерции

Моменты инерции пластины относительно осей Ох и Оу вычисляются по формулам:

, .

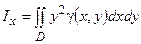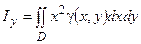Момент инерции относительно начала координат равен

.

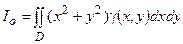6. Геометрические моменты инерции

Полагая в формулах для I_x, I_y и I_o γ(х, у) = 1, получим формулы для вычисления геометрических моментов инерции:

, , .

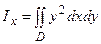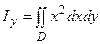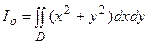Пример 1.1.Вычислить двойной интеграл 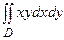, если область D ограничена прямыми y = x, y = 2x, x = 1.

Рис. 1.8

Решение. Построим область интегрирования D (рис.1.8). Область принадлежит первому виду, поэтому интеграл будем вычислять по формуле (1.2). В данном случае a =0, b=1, y₁(x) = x, y₂(x) = 2x, подынтегральная функция - f(x, y) = xy.

.

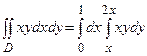Вычислим сначала внутренний интеграл, считая х постоянным, а затем найдем внешний интеграл.

.

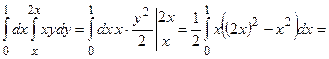
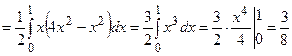Ответ:3/8.

Пример 1.2. Вычислить двойной интеграл 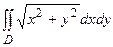, если область D ограничена окружностями x² + y²= x, x² + y²=2x.

Решение. Преобразуем уравнения окружностей:

x² + y²= x Þ

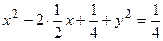Þ

Þ ,

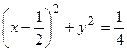Рис. 1.9

x² + y²=2x 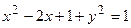Þ

Þ

.

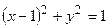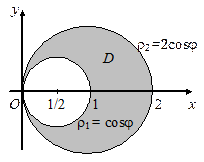
Первая окружность имеет центр в точке (1/2; 0) и радиус 1/2, вторая окружность имеет центр в точке (1; 0) и радиус 1 (рис. 1.9).

Запишем уравнения окружностей в полярных координатах:

x² + y²= x Þ ρ² cos²φ+ ρ² sin²φ = ρcosφ Þ ρ = cosφ;

x² + y²=2x Þ ρ = 2cosφ.

Для точек области D полярный угол jизменяется от - 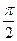до 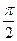, а полярный радиус ρ от кривой ρ₁ = cosφ до кривой ρ₂ = 2cosφ . Найдем интеграл по формуле (1.3).

.

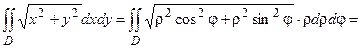
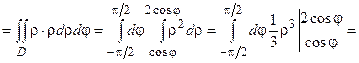
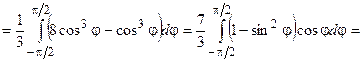
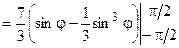
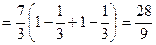Ответ: .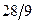

1.2. ТРОЙНЫЕ ИНТЕГРАЛЫ

Рис. 1.10

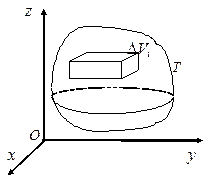Пусть T - ограниченная замкнутая пространственная область, и пусть функция f(x, y, z) определена в области T (рис. 1.10). Разобьем область T произвольно на n частей и обозначим их объемы соответственно ∆V₁, ∆V₂, ∆V₃, . . . , ∆V_n. В каждой частичной области ∆V_i возьмем произвольную точку М_i(x_i, y_i, z_i) и составим интегральную сумму

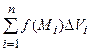. (1.4)

Определение.Тройным интегралом от функции f(x,y,z) по области T называется предел сумм (1.4) для различных разбиений при условии, что наибольший диаметр частей ∆V_i стремится к нулю. Обозначается символом

.

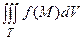Итак,

.
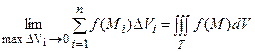