Течение жидкости в узких щелях

Щелевые зазоры являются элементами гидравлических устройств, в которых скорость жидкости не достигает значений, вызывающих её турбулентность. В щелевых зазорах течение жидкости является ламинарным. Как правило, плотность соединения подвижных пар гидроагрегатов обеспечивается выполнением малого (микронного) зазора. Плотность щелевых уплотнений основано на физических свойствах реальных жидкостей оказывать сопротивление деформациям сдвига.

Различают плоские и кольцевые зазоры.

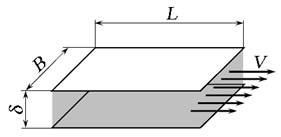
Рис. 3.17. Схема течения жидкости через плоский зазор

Рассмотрим случай плоского зазора, когда течение жидкости через него возникает под действием перепада давления ∆р (рис. 3.17). Расход жидкости в зазоре между пластинами будет равен:

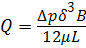, (3.17)

где ∆р – перепад давлениий, под действием которого происходит течение жидкости в зазоре, ;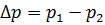

δ, В и L – высота, ширина и длина зазора;

μ – коэффициент динамической вязкости.

Скорость течения жидкости в зазоре .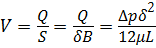

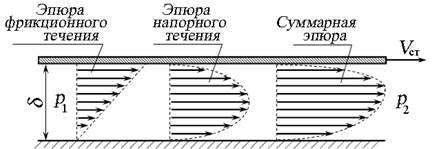
Если одна из стенок, образующих зазор, перемещается параллельно другой с некоторой скоростью V_ст, течение жидкости рассматривают как сумму двух течений:

- так называемого фрикционного течения, образованного перемещением верхней стенки;

- напорного течения, образованного перепадом давлений ∆р.

а)

б)

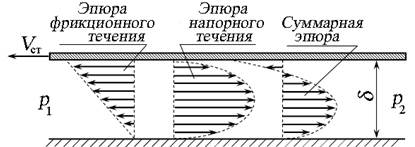
Рис. 3.18. Распределение скоростей в плоском зазоре

с движущейся стенкой и перепадом давления

Распределение скоростей при движении одной из стенок будет зависеть от направления движения стенки (рис. 3.18). В этом случае расход будет учитывать скорость перемещения и направление движения стенки:

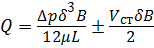. (3.18)

Первое слагаемое уравнения (3.18) определяет напорное течение под действием перепада давления ∆р, второе – фрикционное течение, учитываемое со знаком «+» при совпадении направлений движения жидкости и стенки, со знаком «–» при разнонаправленном движении.

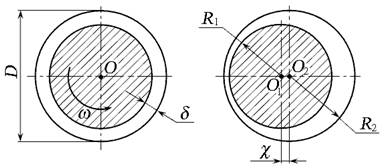
Рис. 3.19. Схема соосного (а) и эксцентричного (б)

расположения цилиндрических поверхностей

Кольцевые зазоры образованы двумя соосно расположенными цилиндрическими поверхностями, например, цилиндр – поршень, золотник – внутренняя поверхность корпуса гидрораспределителя. Расход через кольцевой зазор определяют по формуле (3.18), где B = πD:

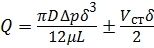. (3.19)

Для определения расхода жидкости в кольцевом зазоре, образованном эксцентричными цилиндрическими поверхностями, пользуются зависимостью:

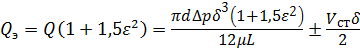, (3.20)

где Q – расход в зазоре при соосном расположении цилиндрических поверхностей;

d – диаметр внутренней цилиндрической поверхности;

ε – относительный эксцентриситет, ;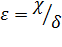

χ – величина эксцентриситета;

δ – номинальный зазор.

Ламинарное движение вязкой жидкости в малом зазоре толщиной δ является основой гидродинамической теории смазки между трущимися поверхностями, в частности, создание смазочного слоя в подшипниках скольжения.

Примеры решения задач

В данном разделе представлены примеры решения простейших задач, связанных с определением параметров движущейся идеальной жидкости. Основными уравнениями, позволяющими определить скорость, расход и давление движущейся идеальной жидкости, являются:

- уравнение постоянства расхода (3.3) ;

- уравнение Бернулли для идеальной жидкости без учёта потерь напора h_пот и коэффициента Кориолиса α (3.8)

.

Правила применения уравнения Бернулли рассмотрены в п. 3.5. Уравнение Бернулли рекомендуется вначале записать в общем виде, затем переписать его с учётом действующих в выбранных сечениях геометрического, гидростатического (или пъезометрического) и скоростного напора относительно плоскости сравнения. Члены уравнения, равные нулю, следует исключить. Также необходимо чётко представлять разницу между избыточным, вакуумметрическим и абсолютным давлением.

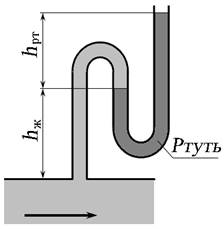
Рис. 3.20. Ртутный пъезометр

Если сечение выбирается в месте подключения ртутного пъезометра (рис. 3.20), то пъезометрическая высота будет равна:

,

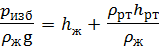где ρ_ж и ρ_рт – плотность жидкости в трубопроводе и ртути в пъезометре;

h_ж и h_рт – высота столба жидкости и ртути в пъезометре.

Задачи, связанные с течением жидкости в узких щелях, решают по формулам, представленным в п. 3.8.

Задача 3.9.1. Поршень диаметром d_п = 8 см перемещается со скоростью V_п под действием силы F = 0,4 кН. Жидкость плотностью ρ = 870 кг/м³ под действием поршня из правой части гидроцилиндра перемещается в бак, открытый в атмосферу. Определить скорость перемещения поршня V_п, если высота h = 9,4 м.

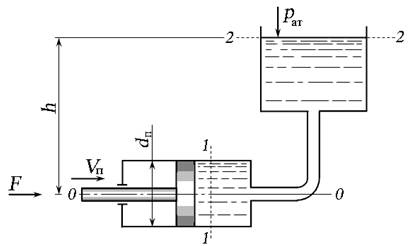
Рис. 3.21. Схема к задаче 3.9.1

Плоскость сравнения 0 – 0 выбираем по оси гидроцилиндра. Сечение 1 – 1 выбираем по живому сечению жидкости в гидроцилиндре, причём параметры уравнения, относящиеся к этому сечению, относятся к центру тяжести сечения. Сечение 2 – 2 выбираем по свободной поверхности жидкости, где давление – только атмосферное (избыточное р_изб = 0), скорость жидкости V₂ ≈ 0. Составим уравнение Бернулли, где давление будем учитывать в избыточной системе отсчёта.

Для сечения 1 – 1:

- геометрическая высота z₁ = 0, так как центр тяжести сечения совпадает с плоскостью сравнения;

- избыточное давление создаётся силой 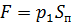, откуда

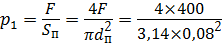= 80 кПа;

- жидкость в сечении движется с той же скоростью, что и поршень (V₁ = V_п), поэтому скоростной напор запишем как .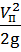

Для сечения 2 – 2:

- геометрическая высота z₂ = h;

- избыточное давление р₂ = 0;

- скорость V₂ = 0.

Составим уравнение Бернулли:

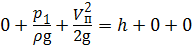, откуда

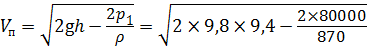= 0,576 м/с.

Задача 3.9.2. Определить вакуумметрическое давление в баке р_вак, при котором скорость течения потока жидкости в трубопроводе составит V_тр = 1,2 м/с. Высота h = 3,2 м, плотность жидкости ρ = 870 кг/м³. Высота уровня жидкости в пъезометре составляет h_п = 0,64 м.

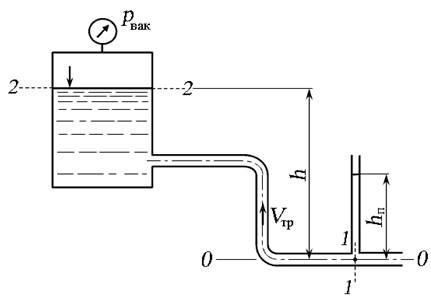
Рис. 3.22. Схема к задаче 3.9.2

Плоскость сравнения 0 – 0 выберем по оси трубопровода в нижней его части. Сечение 1 – 1 выберем по установленному в нижней части трубы пъезометру, сечение 2 – 2 выберем по свободной поверхности жидкости в баке. Составим уравнение Бернулли, где давление будем учитывать в избыточной системе отсчёта.

Для сечения 1 – 1:

- геометрическая высота z₁ = 0, так как центр тяжести сечения совпадает с плоскостью сравнения;

- пъезометрическая высота в сечении ;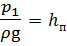

- скорость течения жидкости в трубопроводе V₁ = V_тр.

Для сечения 2 – 2:

- геометрическая высота z₂ = h;

- вакуумметрическая высота ;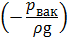

- скорость V₂ = 0.

Составим уравнение Бернулли:

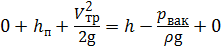, откуда

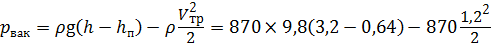= 21,2 кПа.

Задача 3.9.3. Определить утечки через радиальные зазоры в шестерённом насосе вследствие разности давлений в нагнетательной и всасывающей полости. Высота каждого зазора δ = 0,09 мм, длина зазора L = 2 мм, ширина В = 30 мм, перепад давлений ∆р = 1,32 МПа, наружный диаметр шестерни D = 62 мм, частота вращения n = 1450 об/мин, вязкость масла μ = 0,012 Па∙с.

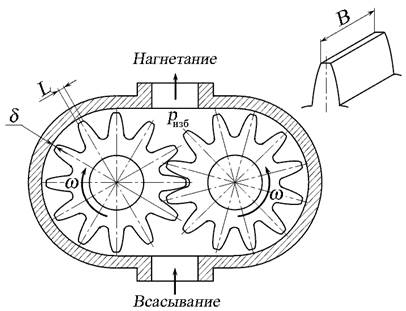
Рис. 3.23. Схема к задаче 3.9.3

Считаем, что число зубьев, образующих радиальные зазоры слева и справа, одинаковы, и равны N = 7 с каждой стороны, размеры зазоров также одинаковы. Поэтому величина утечек слева и справа одинакова. Перепад давлений, приходящийся на один зазор, равен

.

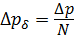Общий расход через зазоры равен сумме расходов слева и справа

.

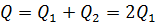Расход через зазоры слева или справа равен согласно (3.18)

.

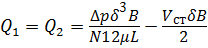Окружная скорость 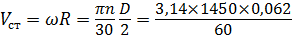= 4,7 м/с.

Тогда

=

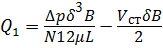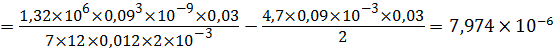м³/с.

Общий расход через зазоры вследствие утечек

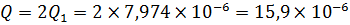м³/с ≈ 0,016 л/с.