Взаимодействие параллельных токов
Магнитное поле (см. § 109) оказы- вает на рамку с током ориентирующее действие. Следовательно, вращающий момент, испытываемый рамкой, есть результат действия сил на отдельные ее элементы. Обобщая результаты иссле- дования действия магнитного поля на различные проводники с током, А. Ам- пер установил, что сила  с которой магнитное поле действует на элемент проводника
с которой магнитное поле действует на элемент проводника  с током, находящегося в магнитном поле, равна
с током, находящегося в магнитном поле, равна
 (111.1)
(111.1)
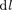 где
где  — вектор, по модулю равный
— вектор, по модулю равный
и совпадающий по направлению с то- ком,  — вектор магнитной индукции. Направление вектора
— вектор магнитной индукции. Направление вектора  может быть найдено, согласно (111.1), по общим правилам векторного произведения, откуда следует правило левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор
может быть найдено, согласно (111.1), по общим правилам векторного произведения, откуда следует правило левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор  а че- тыре вытянутых пальца — по направ- лению тока в проводнике, то отогнутый большой палец покажет направление
а че- тыре вытянутых пальца — по направ- лению тока в проводнике, то отогнутый большой палец покажет направление
силы, действующей на ток.
Модуль силы Ампера [см. (111.1)] вычисляется по формуле
 (111.2)
(111.2)
где а — угол между векторами 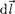 и dB. Закон Ампера применяется для оп- ределения силы взаимодействия двух токов. Рассмотрим два бесконечных прямолинейных параллельных тока
и dB. Закон Ампера применяется для оп- ределения силы взаимодействия двух токов. Рассмотрим два бесконечных прямолинейных параллельных тока  и
и 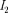 (на рис. 169 токи направлены пер- пендикулярно плоскости чертежа к нам), расстояние между которыми равно R. Каждый из проводников создает магнит- ное поле, которое действует по закону
(на рис. 169 токи направлены пер- пендикулярно плоскости чертежа к нам), расстояние между которыми равно R. Каждый из проводников создает магнит- ное поле, которое действует по закону
Ампера на другой проводник с током.

Рис. 169
Рассмотрим, с какой силой действу- ет магнитное поле тока 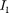 на элемент dl второго проводника с током
на элемент dl второго проводника с током 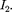 Ток
Ток 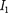 создает вокруг себя магнитное поле, линии индукции которого представля- ют собой концентрические окружнос- ти. Направление вектора
создает вокруг себя магнитное поле, линии индукции которого представля- ют собой концентрические окружнос- ти. Направление вектора  определя- ется правилом правого винта, его мо- дуль по формуле (110.5) равен
определя- ется правилом правого винта, его мо- дуль по формуле (110.5) равен
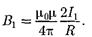
Направление силы  с которой поле
с которой поле 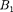 действует на участок
действует на участок  второ- го тока, определяется поправилу левой руки иуказано на рисунке. Модуль силы, согласно (111.2), с учетом того, что угол амежду элементами тока
второ- го тока, определяется поправилу левой руки иуказано на рисунке. Модуль силы, согласно (111.2), с учетом того, что угол амежду элементами тока  и вектором
и вектором  прямой, равен
прямой, равен

Подставляя значение для  получим
получим
 (111.3)
(111.3)

 Рассуждая аналогично, можно пока- зать, что сила которой магнитное поле тока
Рассуждая аналогично, можно пока- зать, что сила которой магнитное поле тока  действует на элемент dl первого проводника с током
действует на элемент dl первого проводника с током  направ- лена в противоположную сторону и модулю равна
направ- лена в противоположную сторону и модулю равна
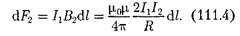 |
Сравнение выражений (111.3) и (111.4) показывает, что

т. е. двапараллельныхтокаодинакового направленияпритягиваютсядругкдру- гу с силой
 |
Если токи имеют противоположные направления, то, используя правило ле- вой руки, можно показать, что между ними действует сила отталкивания, оп- ределяемая по формуле (111.5).
§ 112. Магнитная постоянная. Единицы магнитной индукции и напряженности магнитногополя
Если два параллельных проводника с током находятся в вакууме  = 1), то сила взаимодействия на единицу дли- ны проводника, согласно
= 1), то сила взаимодействия на единицу дли- ны проводника, согласно  равна
равна
 (112.1)
(112.1)
 Для нахождения числового значения
Для нахождения числового значения  воспользуемся определением ампера, согласно которому
воспользуемся определением ампера, согласно которому  = 2 • Н/м при
= 2 • Н/м при  =
=  = 1 А и R — 1 м. Подставив это значение в формулу (112.1), получим
= 1 А и R — 1 м. Подставив это значение в формулу (112.1), получим

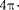 =
=  Н/А2 =
Н/А2 =  Гн/м.
Гн/м.
Единица индуктивности — генри
(Гн) (см. § 126).'
 Закон Ампера позволяет определить единицу магнитной индукции В. Пред- положим, что элемент проводника
Закон Ампера позволяет определить единицу магнитной индукции В. Пред- положим, что элемент проводника  с током /перпендикулярен направлению магнитного поля. Тогда закон Ампера [см. (111.2)] запишется в виде
с током /перпендикулярен направлению магнитного поля. Тогда закон Ампера [см. (111.2)] запишется в виде
— 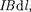 откуда
откуда

Единица магнитной индукции — тесла (Тл): 1 Тл — магнитная индук- ция такого однородного магнитного поля, которое действует с силой 1 Н на каждый метр длины прямолинейного проводника, расположенного перпен- дикулярно направлению поля, если по этому проводнику течет ток 1 А:
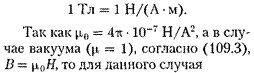
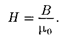
Единицанапряженностимагнитного поля — ампер на метр(А/м): 1 А/м — напряженность такого поля, магнитная индукция которого в вакууме равна
 •
•  Тл.
Тл.
§ 113. Магнитное поле движущегося заряда
Каждый проводник с током создает в окружающем пространстве магнитное поле. Электрический ток представляет собой упорядоченное движение элект- рических зарядов, поэтому можно ска- зать, что любой движущийся в вакууме или среде заряд создает вокруг себя магнитное поле. В результате обобще- ния опытных данных был установлен закон, определяющий поле  точечно- го заряда Q, свободно движущегося с нерелятивистской скоростью v. Под свободным движением заряда понима- ется его движение с постоянной скоро- стью. Этот закон выражается формулой
точечно- го заряда Q, свободно движущегося с нерелятивистской скоростью v. Под свободным движением заряда понима- ется его движение с постоянной скоро- стью. Этот закон выражается формулой
 (113.1)
(113.1)

 где — радиус-вектор, проведенный от заряда Q точке наблюдения М (рис. 170).
где — радиус-вектор, проведенный от заряда Q точке наблюдения М (рис. 170).
 Согласно выражению (113.1), век- тор В направлен перпендикулярно плоскости, в которой расположены век- торы v и г, а именно: его направление совпадает с направлением поступатель- ного движения правого винта при его вращении от v г. Вектор
Согласно выражению (113.1), век- тор В направлен перпендикулярно плоскости, в которой расположены век- торы v и г, а именно: его направление совпадает с направлением поступатель- ного движения правого винта при его вращении от v г. Вектор  представ- ляет собой псевдовектор.
представ- ляет собой псевдовектор.
Модуль магнитной индукции (113.1) вычисляется по формуле



 где а — угол между векторами И Сравнивая выражения (110.1) и
где а — угол между векторами И Сравнивая выражения (110.1) и
(113.1), видим, что движущийся заряд по своим магнитным свойствам экви- валентен элементу тока.
 Приведенные закономерности (113.1) и
Приведенные закономерности (113.1) и 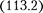 справедливы лишь для малых скоростей (v с) движущихся зарядов, когда электрическое поле свободно дви- жущегося заряда можно считать элект- ростатическим, т. е. создаваемым непод- вижным зарядом, находящимся в той точке, где в данный момент времени расположен движущийся заряд.
справедливы лишь для малых скоростей (v с) движущихся зарядов, когда электрическое поле свободно дви- жущегося заряда можно считать элект- ростатическим, т. е. создаваемым непод- вижным зарядом, находящимся в той точке, где в данный момент времени расположен движущийся заряд.
Формула (113.1) определяет маг- нитную индукцию положительного за- ряда, движущегося со скоростью v. Если движется отрицательный заряд, то Q надо заменить на — Q. Скорость v — от- носительная скорость, т. е. скорость от- носительно наблюдателя. Вектор  в рассматриваемой системе отсчета зави- сит как от времени, так и от положения точки М наблюдения. Поэтому следует подчеркнуть относительный характер магнитного поля движущегося заряда. Впервые поле движущегося заряда удалось обнаружить американскому физику Г.Роуланду (1848-1901). Окончательно этот факт был установлен
в рассматриваемой системе отсчета зави- сит как от времени, так и от положения точки М наблюдения. Поэтому следует подчеркнуть относительный характер магнитного поля движущегося заряда. Впервые поле движущегося заряда удалось обнаружить американскому физику Г.Роуланду (1848-1901). Окончательно этот факт был установлен
Рис. 170
 профессором Московского университе- та А.А.Эйхенвальдом (1863—1944), изучившим магнитное поле конвекци- онного тока, а также магнитное поле связанных зарядов поляризованного диэлектрика. Магнитное поле свобод- но движущихся зарядов было измере- но академиком А.Ф.Иоффе, доказав- шим эквивалентность, в смысле воз- буждения магнитного поля, электрон- ного пучка и тока проводимости.
профессором Московского университе- та А.А.Эйхенвальдом (1863—1944), изучившим магнитное поле конвекци- онного тока, а также магнитное поле связанных зарядов поляризованного диэлектрика. Магнитное поле свобод- но движущихся зарядов было измере- но академиком А.Ф.Иоффе, доказав- шим эквивалентность, в смысле воз- буждения магнитного поля, электрон- ного пучка и тока проводимости.
§ 114. Действие магнитного поля на движущийся заряд
Опыт показывает, что магнитное поле действует не только на проводни- ки с током (см. § 111), но и на отдель- ные заряды, движущиеся в магнитном поле. Сила, действующая на электри- ческий заряд Q, движущийся в магнит- ном поле со скоростью v, называется силой Лоренца и выражается форму- лой
 (114.1)
(114.1)
где  — индукция магнитного поля, в котором заряд движется.
— индукция магнитного поля, в котором заряд движется.
Направление силы Лоренца опреде- ляется с помощью правила левойруки: если ладонь левой руки расположить так, чтобы в нее входил вектор В, а четыре вытянутых пальца направить вдоль вектора v (для Q > 0 направле- ния I и v совпадают, для Q < 0 — про- тивоположны), то отогнутый большой палец покажет направление силы, дей- ствующей на положительныйзаряд. На рис. 171 показана взаимная ориентация векторов v, В (поле направлено к нам,
 Рис. 171 Это выражение называется форму- лой Лоренца. Скорость v в этой фор- муле есть скорость заряда относитель- но магнитного поля.
Рис. 171 Это выражение называется форму- лой Лоренца. Скорость v в этой фор- муле есть скорость заряда относитель- но магнитного поля.
на рисунке показано точками) и F для положительного и отрицательного заря- дов. На отрицательный заряд сила дей- ствует в противоположном направле- нии. Модуль силы Лоренца [см. (114.1)]

где а — угол между v и 
Отметим еще раз (см. § 109), что маг- нитное поле не действует на покоящий- ся электрический заряд. В этом суще- ственное отличие магнитного поля от электростатического. Магнитное поле действуеттольконадвижущиесявнем заряды.
Выражение (114.1) для силы Лорен- ца может быть использовано (наравне с другими, см. § 109) для определения вектора магнитной индукции 
Сила Лоренца всегда перпендику- лярна скорости движения заряженной частицы, поэтому она изменяет только направление этой скорости, не меняя ее модуля. Следовательно, сила Лоренца работы не совершает. Иными словами, постоянное магнитное поле не соверша- ет работы над движущейся в нем заря- женной частицей и кинетическая энер- гия этой частицы при движении в маг- нитном поле не изменяется.
 Если на движущийся электрический заряд магнитного поля с индук- цией
Если на движущийся электрический заряд магнитного поля с индук- цией 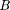 действует и электрическое поле с напряженностью Е, то результирую- щая сила F, приложенная к заряду, рав- на векторной сумме сил — силы, дей- ствующей со стороны электрического поля, и силы Лоренца:
действует и электрическое поле с напряженностью Е, то результирую- щая сила F, приложенная к заряду, рав- на векторной сумме сил — силы, дей- ствующей со стороны электрического поля, и силы Лоренца:
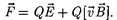
§ 115. Движение заряженных частиц в магнитном поле
Выражение для силы Лоренца (114.1) позволяет найти ряд закономер- ностей движения заряженных частиц в магнитном поле. Направление силы Лоренца и направление вызываемого ею отклонения заряженной частицы в магнитном поле зависят от знака заря- да Q частицы. На этом основано опре- деление знака заряда частиц, движу- щихся в магнитных полях.
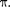 Для вывода общих закономерностей будем считать, что магнитное поле од- нородно и на частицы электрические поля не действуют. Если заряженная частица движется в магнитном поле со скоростью v вдоль линий магнитной индукции, то угол а между векторами v и
Для вывода общих закономерностей будем считать, что магнитное поле од- нородно и на частицы электрические поля не действуют. Если заряженная частица движется в магнитном поле со скоростью v вдоль линий магнитной индукции, то угол а между векторами v и  равен 0 или Тогда по формуле (114.1) сила Лоренца равна нулю, т.е. магнитное поле на частицу не действу- ет и она движется равномерно и прямо- линейно.
равен 0 или Тогда по формуле (114.1) сила Лоренца равна нулю, т.е. магнитное поле на частицу не действу- ет и она движется равномерно и прямо- линейно.
 Если заряженная частица движется в магнитном поле со скоростью v, пер- пендикулярной вектору
Если заряженная частица движется в магнитном поле со скоростью v, пер- пендикулярной вектору 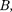 то сила Ло- ренца F = Q
то сила Ло- ренца F = Q 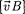 постоянна по модулю и нормальна к траектории частицы. Со- гласно второму закону Ньютона, эта сила создает центростремительное ус- корение. Отсюда следует, что частица будет двигаться по окружности, ради- ус которой определяется из условия
постоянна по модулю и нормальна к траектории частицы. Со- гласно второму закону Ньютона, эта сила создает центростремительное ус- корение. Отсюда следует, что частица будет двигаться по окружности, ради- ус которой определяется из условия
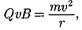 откуда
откуда
 (115.1)
(115.1)
Период вращения частицы, т. е. вре- мя Г, за которое она совершает один полный оборот,

Подставив сюда выражение (115.1), получим
 (115.2)
(115.2)
т.е. период вращения частицы в одно- родном магнитном поле определяется только величиной, обратной удельному
заряду ( —) частицы, и магнитной ин-
 дукцией поля, но не зависит от ее ско- рости (при v с). На этом основано действие циклических ускорителей за- ряженных частиц (см. §
дукцией поля, но не зависит от ее ско- рости (при v с). На этом основано действие циклических ускорителей за- ряженных частиц (см. § 
 Если скорость v заряженной
Если скорость v заряженной
 цы направлена под углом к вектору (рис. 172), то ее движение можно пред- ставить как наложение двух движений:
цы направлена под углом к вектору (рис. 172), то ее движение можно пред- ставить как наложение двух движений:
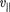
 1) равномерного прямолинейного дви- жения вдоль поля со скоростью
1) равномерного прямолинейного дви- жения вдоль поля со скоростью
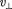



 = v cos a; 2) равномерного движения со скоростью = v sin по окружности в плоскости, перпендикулярной полю. Радиус окружности определяется фор- мулой (115.1) (в данном случае надо за- менить v на = Поэтому тра- ектория заряженной частицы - спи- раль, ось которой параллельна магнит- ному полю (см. рис. 172). Шаг винто- вой линии
= v cos a; 2) равномерного движения со скоростью = v sin по окружности в плоскости, перпендикулярной полю. Радиус окружности определяется фор- мулой (115.1) (в данном случае надо за- менить v на = Поэтому тра- ектория заряженной частицы - спи- раль, ось которой параллельна магнит- ному полю (см. рис. 172). Шаг винто- вой линии
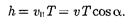
Подставив в последнее выражение (115.2), получим

Направление, в котором закручива- ется спираль, зависит от знака заряда частицы.
Рис. 172

 Если скорость v заряженной части- цы составляет угол а с направлением вектора неоднородного магнитного поля, индукция которого возрастает в направлении движения частицы, то и h уменьшаются с увеличением В. На этом основана фокусировка заряжен- ных частиц в магнитном поле.
Если скорость v заряженной части- цы составляет угол а с направлением вектора неоднородного магнитного поля, индукция которого возрастает в направлении движения частицы, то и h уменьшаются с увеличением В. На этом основана фокусировка заряжен- ных частиц в магнитном поле.
§116.Ускорителизаряженных частиц
Ускорителямизаряженных частиц называются устройства, в которых под действием электрических и магнитных полей создаются и управляются пучки высокоэнергетичных заряженных час- тиц (электронов, протонов, мезонов и т.д.).
Любой ускоритель характеризуется типом ускоряемых частиц, энергией, сообщаемой частицам, разбросом час- тиц по энергиям и интенсивностью пуч- ка. Ускорители делятся на непрерыв- ные (из них выходит равномерный по времени пучок) и импульсные (из них частицы вылетают порциями — им- пульсами). Последние характеризуют- ся длительностью импульса. По форме траектории и механизму ускорения ча-


 цускорители делятсяна циклические индукционные. В ли- нейных ускорителях траектории дви- жения частиц близки к прямым лини- ям, в циклических и индукционных — траекториями частиц являются окруж- ности или спирали.
цускорители делятсяна циклические индукционные. В ли- нейных ускорителях траектории дви- жения частиц близки к прямым лини- ям, в циклических и индукционных — траекториями частиц являются окруж- ности или спирали.
Рассмотрим некоторые типы уско- рителей заряженных частиц.


 1. Линейныйускоритель.Ускорение частиц осуществляется электростатичес- ким полем, создаваемым, например, вы- соковольтным генератором Ван-де-Гра- афа (см. § 92). Заряженная частица про- ходит поле однократно: заряд Q, прохо- дя разность потенциалов — при- обретает энергию W= — Та- ким способом частицы ускоряются до МэВ. Их дальнейшее ускорение с помощью источников постоянного на- пряжения невозможно из-за утечки за-
1. Линейныйускоритель.Ускорение частиц осуществляется электростатичес- ким полем, создаваемым, например, вы- соковольтным генератором Ван-де-Гра- афа (см. § 92). Заряженная частица про- ходит поле однократно: заряд Q, прохо- дя разность потенциалов — при- обретает энергию W= — Та- ким способом частицы ускоряются до МэВ. Их дальнейшее ускорение с помощью источников постоянного на- пряжения невозможно из-за утечки за-
рядов, пробоев и т.д.
2. Линейный резонансный ускори- тель.Ускорение заряженных частиц осуществляется переменным электри- ческим полем сверхвысокой частоты, синхронно изменяющимся с движением частиц. Таким способом протоны уско- ряются до энергий порядка десятков мегаэлектрон-вольт, электроны — до десятков гигаэлектрон-вольт.
3. Циклотрон— циклический резо- нансный ускоритель тяжелых частиц (протонов, ионов). Его принципиаль- ная схема приведена на рис. 173. Меж- ду полюсами сильного электромагнита
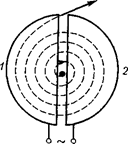 Рис. 173
Рис. 173
помещается вакуумная камера, в кото- рой находятся два электрода (1 и 2) в виде полых металлических полуцилин- дров, или дуантов. К дуантам приложе- но переменное электрическое ноле. Магнитное поле, создаваемое электро- магнитом, однородно и перпендикуляр- но плоскости дуантов.
Если заряженную частицу ввести в центр зазора между дуантами, то она, ускоряемая электрическим и отклоня- емая магнитным полями, войдя в ду- ант 1, опишет полуокружность, радиус которой пропорционален скорости ча- стицы [см. (115.1)]. К моменту ее вы- хода из дуанта 1 полярность напряже- ния изменяется (при соответствующем подборе изменения напряжения между дуантами), поэтому частица вновь ус- коряется и, переходя в дуант 2, описы- вает там уже полуокружность больше- го радиуса и т.д.
Для непрерывного ускорения час- тицы в циклотроне необходимо выпол- нить условие синхронизма (условие
«резонанса») — периоды вращения ча- стицы в магнитном поле и колебаний электрического поля должны быть равны. При выполнении этого усло- вия частица будет двигаться по рас- кручивающейся спирали, получая при каждом прохождении через зазор до- полнительную энергию. На после- днем витке, когда энергия частиц и радиус орбиты доведены до макси- мально допустимых значений, пучок частиц посредством отклоняющего электрического поля выводится из циклотрона.
Циклотроны позволяют ускорять протоны до энергий примерно 25 МэВ. В случае более высоких энергий пери- од вращения частицы оказывается за- висящим от скорости, а именно период вращения увеличивается, в результате чего нарушается условие синхронизма.
Ускорение релятивистских частиц в циклических ускорителях можно, одна- ко, осуществить, если применять пред- ложенный в 1944 г. В.И.Векслером (1907 — 1966) и в 1945 г. американским физиком Э.Мак-Милланом (1907— 1991) принцип автофазировки. Его идея заключается в том, что для ком- пенсации увеличения периода враще- ния частиц, ведущего к нарушению син- хронизма, изменяют либо частоту уско- ряющего электрического, либо индук- цию магнитного полей, либо то и дру- гое. Принцип автофазировки использу- ется в фазотроне, синхротроне и синх- рофазотроне.
4. Фазотрон(синхроциклотрон) — циклический резонансный ускоритель тяжелых заряженных частиц (напри- мер, протонов, ионов,  в ко- тором управляющее магнитное поле постоянно, а частота ускоряющего элек- трического поля медленно изменяется с периодом. Движение частиц в фазо- троне, как и в циклотроне, происходит по раскручивающейся спирали. Час- тицы в фазотроне ускоряются до энер- гий, примерно равных 1 ГэВ (ограни- чения здесь определяются размерами фазотрона, так как с возрастанием ско- рости частиц увеличивается радиус их орбиты).
в ко- тором управляющее магнитное поле постоянно, а частота ускоряющего элек- трического поля медленно изменяется с периодом. Движение частиц в фазо- троне, как и в циклотроне, происходит по раскручивающейся спирали. Час- тицы в фазотроне ускоряются до энер- гий, примерно равных 1 ГэВ (ограни- чения здесь определяются размерами фазотрона, так как с возрастанием ско- рости частиц увеличивается радиус их орбиты).
5. Синхротрон— циклический резо- нансный ускоритель ультрарелятиви- стских электронов, в котором управля- ющее магнитное поле изменяется во времени, а частота ускоряющего элект- рического поля постоянна. Электроны в синхротроне ускоряются до энергий  ГэВ.
ГэВ.
6. Синхрофазотрон— циклический резонансный ускоритель тяжелых заря- женных частиц (протонов, ионов), в ко- тором объединяются свойства фазотро- на и синхротрона, т.е. управляющее магнитное поле и частота ускоряющего
электрического поля одновременно из- меняются во времени так, чтобы ради- ус равновесной орбиты частиц оставал- ся постоянным. Протоны ускоряются в синхрофазотроне до энергий 500 ГэВ.
7. Бетатрон— циклический индук- ционный ускоритель электронов, в ко- тором ускорение осуществляется вих- ревым электрическим полем (см. § 137), индуцируемым переменным магнит- ным полем, удерживающим электроны на круговой орбите. В бетатроне в от- личие от рассмотренных выше ускори- телей не существует проблемы синхро- низации. Электроны в бетатроне ус- коряются до энергий 100 МэВ. При W> 100 МэВ режим ускорения в бета- троне нарушается электромагнитным излучением электронов. Особенно распространены бетатроны на энергии 20-50 МэВ.
§ 117. Эффект Холла
 Эффект
Эффект 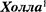 (1879) — это воз- никновение в металле (или полупро- воднике) с током плотностью j, поме- щенном в магнитное поле
(1879) — это воз- никновение в металле (или полупро- воднике) с током плотностью j, поме- щенном в магнитное поле 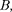 электри- ческого поля в направлении, перпенди- кулярном j.
электри- ческого поля в направлении, перпенди- кулярном j.
Поместим металлическую пластин- ку с током плотностью j в магнитное поле  перпендикулярное
перпендикулярное 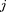 (рис. 174). При данном направлении j скорость носителей тока в металле — электро- нов — направлена справа налево. Элек- троны испытывают действие силы Ло- ренца (см. § 114), которая в данном случае направлена вверх. Таким обра- зом, у верхнего края пластинки воз- никнет повышенная концентрация электронов (он зарядится отрицатель- но), а у нижнего — их недостаток (за-
(рис. 174). При данном направлении j скорость носителей тока в металле — электро- нов — направлена справа налево. Элек- троны испытывают действие силы Ло- ренца (см. § 114), которая в данном случае направлена вверх. Таким обра- зом, у верхнего края пластинки воз- никнет повышенная концентрация электронов (он зарядится отрицатель- но), а у нижнего — их недостаток (за-
1Э. Холл (1855 —1938) — американскийфизик.
 Рис. 174
Рис. 174
рядится положительно). В результате этого между краями пластинки воз- никнет дополнительное поперечное электрическое поле  направленное снизу вверх.
направленное снизу вверх.
Когда напряженность  этого попе- речного поля достигнет такой величи- ны, что его действие на заряды будет уравновешивать силу Лоренца, то уста- новится стационарное распределение зарядов в поперечном направлении.
этого попе- речного поля достигнет такой величи- ны, что его действие на заряды будет уравновешивать силу Лоренца, то уста- новится стационарное распределение зарядов в поперечном направлении.
Тогда

где а — ширина пластинки;  — попе- речная (холловская) разность потенци- алов.
— попе- речная (холловская) разность потенци- алов.
Учитывая, что сила тока I = jS = nevS (S — площадь поперечного сече- нияпластинкитолщиной d, n — концен- трация электронов, v —средняя ско- рость упорядоченного движения элек- тронов), получим
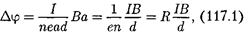 |
т.е. холловская поперечная разность потенциалов пропорциональна магнит- ной индукции В, силе тока 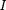 и обратно пропорциональна толщине пластинки d. Вформуле (117.1)
и обратно пропорциональна толщине пластинки d. Вформуле (117.1)  — постоян-
— постоян-
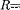 ная Холла, зависящая от вещества.
ная Холла, зависящая от вещества.
Поизмеренному значению постоян- ной Холла можно: 1) определить кон- центрацию носителей тока в проводни-
ке (при известных характере проводи- мости и заряде носителей); 2) судить о природе проводимости полупроводни- ков (см. § 242, 243), так как знак посто- янной Холла совпадает со знаком заря- да е носителей тока. Поэтому эффект Холла — наиболее эффективный метод изучения энергетического спектра но- сителей тока в металлах и полупровод- никах. Он применяется также для умно- жения постоянных токов в аналоговых вычислительных машинах, в измери- тельной технике (датчики Холла) и т. д.
§ 118. Циркуляция вектора в магнитного поля в вакууме
Аналогично циркуляции вектора напряженности электростатического поля (см. § 83) вводят циркуляцию век- тора магнитной индукции. Циркуляци- ей вектора В по заданному замкнуто- му контуру называется интеграл
 |
где  — вектор элементарной длины контура, направленной вдоль обхода контура; В cos a — составляющая вектора в направлении касательной к контуру (с учетом выбранного на- правления обхода); а — угол между век- торами и
— вектор элементарной длины контура, направленной вдоль обхода контура; В cos a — составляющая вектора в направлении касательной к контуру (с учетом выбранного на- правления обхода); а — угол между век- торами и 
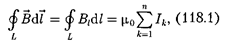

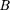

 Закон полного тока для магнит- ного поля в вакууме {теорема о цир- куляции вектора
Закон полного тока для магнит- ного поля в вакууме {теорема о цир- куляции вектора  циркуляция век- тора по произвольному замкнутому контуру равна произведению магнит- ной постоянной на алгебраическую сумму токов, охватываемых этим кон- туром:
циркуляция век- тора по произвольному замкнутому контуру равна произведению магнит- ной постоянной на алгебраическую сумму токов, охватываемых этим кон- туром:

Рис. 175
где п — число проводников с токами, охватываемых контуром L произволь- ной формы.
Каждый токучитывается столько раз, сколько раз он охватывается кон- туром. Положительным считается ток, направление которого образует с на- правлением обхода по контуру право- винтовую систему; ток противополож- ного направления считается отрица- тельным. Например, для системы то- ков, изображенных на рис. 175,
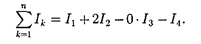 |
Выражение (118.1) справедливо только для поля в вакууме, поскольку, как будет доказано ниже, для поля в веществе необходимо учитывать моле- кулярные токи.
 Продемонстрируем справедливость теоремы о циркуляции вектора
Продемонстрируем справедливость теоремы о циркуляции вектора  на примере магнитного поля прямого то- ка /, перпендикулярного плоскости чер- тежа и направленного к нам (рис. 176). Представим себе замкнутый контур в виде окружности радиуса В каждой
на примере магнитного поля прямого то- ка /, перпендикулярного плоскости чер- тежа и направленного к нам (рис. 176). Представим себе замкнутый контур в виде окружности радиуса В каждой
 Рис. 176
Рис. 176
точке этого контура вектор  одинаков по модулю и направлен по касательной к окружности (она является и линией магнитной индукции). Следовательно, циркуляция вектора
одинаков по модулю и направлен по касательной к окружности (она является и линией магнитной индукции). Следовательно, циркуляция вектора  равна
равна
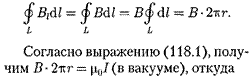 |
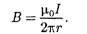
Таким образом, исходя из теоремы о циркуляции вектора  получили вы- ражение для магнитной индукции поля прямого тока, выведенное выше [см. (110.5)].
получили вы- ражение для магнитной индукции поля прямого тока, выведенное выше [см. (110.5)].
 Сравнивая выражения
Сравнивая выражения  и для циркуляции векторов Ё и видим, что между ними существует
и для циркуляции векторов Ё и видим, что между ними существует
принципиальное различие. Циркуляция вектора Е электростатического поля всегда равна нулю, т.е. электростати- ческое поле является потенциальным. Циркуляция вектора В магнитного поля не равна нулю. Такое поле назы- вается вихревым.
Теорема о циркуляции вектора 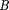 имеет в учении о магнитном поле такое же значение, как теорема Гаусса в элек- тростатике, так как позволяет находить магнитную индукцию поля без приме- нения закона Био — Савара
имеет в учении о магнитном поле такое же значение, как теорема Гаусса в элек- тростатике, так как позволяет находить магнитную индукцию поля без приме- нения закона Био — Савара 
§ 119. Магнитные поля соленоида итороида
Рассчитаем, применяя теорему о циркуляции, индукцию магнитного поля внутри соленоида. Рассмотрим со- леноиддлиной/, имеющий 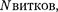 по которому течет ток (рис. 177). Длину соленоида считаем во много раз боль-
по которому течет ток (рис. 177). Длину соленоида считаем во много раз боль-

Рис. 177
 ше, чем диаметр его витков, т.е. рас- сматриваемый соленоид бесконечно длинный. Экспериментальное изуче- ние магнитного поля соленоида (см. рис. 164,
ше, чем диаметр его витков, т.е. рас- сматриваемый соленоид бесконечно длинный. Экспериментальное изуче- ние магнитного поля соленоида (см. рис. 164, 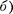 показывает, что внутри со- леноида является однородным, вне соленоида — неоднородным и очень слабым.
показывает, что внутри со- леноида является однородным, вне соленоида — неоднородным и очень слабым.
На рис. 177 представлены линии магнитной индукции внутри и вне со- леноида. Чем соленоид длиннее, тем меньше магнитная индукция вне его. Поэтому приближенно можно считать, что поле бесконечно длинного солено- ида сосредоточено целиком внутри него, а полем вне соленоида можно пре- небречь.
 Для нахождения магнитной индук- ции В выберем замкнутый прямоуголь- ный контур ABCDA, как показано на рис. 177. Циркуляция вектора
Для нахождения магнитной индук- ции В выберем замкнутый прямоуголь- ный контур ABCDA, как показано на рис. 177. Циркуляция вектора  по зам- кнутому контуру А, охватываю- щему все N витков, согласно (118.1), равна
по зам- кнутому контуру А, охватываю- щему все N витков, согласно (118.1), равна
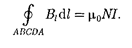
 Рис. 178
Рис. 178
Интеграл по ABCDA можно пред- ставить в виде четырех интегралов: по АВ, ВС, CD и DA. На участках А В и CD контур перпендикулярен линиям маг- нитной индукции и 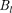 = 0. На участке вне соленоида В = 0. На участке DA циркуляция вектора
= 0. На участке вне соленоида В = 0. На участке DA циркуляция вектора 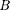 равна
равна 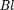 (учас- ток контура совпадает с линией магнит- ной индукции); следовательно,
(учас- ток контура совпадает с линией магнит- ной индукции); следовательно,
 (119.1)
(119.1)
Из (119.1) приходим к выражению для магнитной индукции поля внутри соленоида (в вакууме):
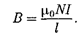 (119.2)
(119.2)
Таким образом, поле внутри солено- ида однородно (краевыми эффектами в областях, прилегающих к торцам соле- ноида, при расчетах пренебрегают). Од- нако отметим, что вывод этой форму- лы не совсем корректен (линии магнит- ной индукции замкнуты, и интеграл по внешнему участку магнитного поля строго нулю не равен). Корректно рас- считать поле внутри соленоида можно, применяя закон  —
— 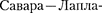 са; в результате получается та же фор- мула (119.2).
са; в результате получается та же фор- мула (119.2).
Важное значение для практики име- ет также магнитное поле тороида — кольцевой катушки, витки которой на- мотаны на сердечник, имеющий форму тора (рис. 178). Магнитное поле, как показывает опыт, сосредоточено внут- ри тороида, вне его поле отсутствует.
 Линии магнитной индукции в дан- ном случае, как следует из соображений симметрии, есть окружности, центры которых расположены по оси тороида. В качестве контура выберем одну такую окружность радиусом Тогда, по тео- реме о циркуляции (118.1),
Линии магнитной индукции в дан- ном случае, как следует из соображений симметрии, есть окружности, центры которых расположены по оси тороида. В качестве контура выберем одну такую окружность радиусом Тогда, по тео- реме о циркуляции (118.1),  =
=
 откуда следует, что магнитная индукция внутри тороида (в вакууме)
откуда следует, что магнитная индукция внутри тороида (в вакууме)
 |
где N — число витков тороида.
 Если контур проходит вне тороида, то токов он не охватывает и В • 0. Это означает, что поле вне тороида от- сутствует (что показывает и опыт).
Если контур проходит вне тороида, то токов он не охватывает и В • 0. Это означает, что поле вне тороида от- сутствует (что показывает и опыт).
§ 120. Поток вектора магнитной индукции.
Теорема Гаусса для поля 
Потоком вектора магнитной ин- дукции (магнитным потоком) через площадку  называется скалярная фи- зическая величина, равная
называется скалярная фи- зическая величина, равная
 |
где  — В cos a — проекция вектора
— В cos a — проекция вектора  на направление нормали к площадке
на направление нормали к площадке 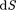 (а —угол между векторами п
(а —угол между векторами п  dS =
dS =


 =
=  — вектор, модуль которого ра- вен dS, анаправление его совпадает с направлением п площадке.
— вектор, модуль которого ра- вен dS, анаправление его совпадает с направлением п площадке.
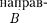 Поток вектора может быть как по- ложительным, так и отрицательным в зависимости от знака cos а (определя- ется выбором положительного
Поток вектора может быть как по- ложительным, так и отрицательным в зависимости от знака cos а (определя- ется выбором положительного

 ления нормали п). Поток вектора свя- зывают с контуром, по которому течет ток. В таком случае положительное на- правление нормали к контуру нами уже определено (см. § 109): оно связывает- ся с током правилом правого винта. Следовательно, магнитный созда- ваемый контуром через поверхность, ограниченную им самим, поло- жителен.
ления нормали п). Поток вектора свя- зывают с контуром, по которому течет ток. В таком случае положительное на- правление нормали к контуру нами уже определено (см. § 109): оно связывает- ся с током правилом правого винта. Следовательно, магнитный созда- ваемый контуром через поверхность, ограниченную им самим, поло- жителен.
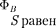 Поток вектора магнитной индук- ции через произвольную поверх- ность
Поток вектора магнитной индук- ции через произвольную поверх- ность
(120.2)
 Для однородного поля и плоской поверхности, расположенной перпен- дикулярно вектору
Для однородного поля и плоской поверхности, расположенной перпен- дикулярно вектору 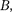
 — В — const и
— В — const и
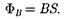 |
Из этой формулы определяется еди- ница магнитного потока вебер(Вб): 1 Вб —магнитный поток, проходящий сквозь плоскую поверхность площадью 1м2, расположенную перпендикулярно однородному магнитному полю, индук
