Тяготение. элементы теории поля

§ 22. Законы Кеплера. Закон всемирного тяготения

Еще в глубокой древности было за- мечено, что в отличие от звезд, которые неизменно сохраняют свое взаимное расположение в пространстве в течение столетий, планеты описывают среди звезд сложнейшие траектории. Для объяснения петлеобразного движения планет древнегреческий ученый К. Пто- лемей (II в. н.э.), считая Землю распо- ложенной в центре Вселенной, предпо- ложил, что каждая из планет движется по малому кругу (эпициклу), центр ко- торого равномерно движется по боль- шому кругу, в центре которого находит- ся Земля. Эта концепция получила на-

звание птолемеевой геоцентрической системы мира.

В начале XVI в. польским астроно- мом Н.Коперником (1473 — 1543) обо- снована гелиоцентрическая система (см. § 5), согласно которой движения небесных тел объясняются движением Земли (а также других планет) вокруг Солнца и суточным вращением Земли. Теория и наблюдения Коперника вос- принимались как занимательная фан- тазия.

К началу XVII столетия большин- ство ученых, однако, убедилось в спра- ведливости гелиоцентрической систе- мы мира. И. Кеплер (немецкий ученый, 1571 — 1630), обработав и уточнив ре- зультаты многочисленных наблюдений

датского астронома Т. Браге (1546 — 1601), эмпирически установил законы движения планет:

1. Каждая планета движется по эл- липсу, в одном из фокусов которого на- ходится Солнце.

2. Радиус-вектор планеты за равные промежутки времени описывает одина- ковые площади.

3. Квадраты периодов обращения планет вокруг Солнца относятся как кубы больших полуосей их орбит.

Впоследствии И.Ньютон, изучая движение небесных тел, на основании законов Кеплера и основных законов динамики установил закон всемирно- го тяготения: между любыми двумя материальными точками действует сила взаимного притяжения, прямо пропорциональная произведению масс этих точек и и обратно пропор- циональная квадрату расстояния меж- ду ними (r2):

(22.1)

Эта сила называется гравитацион- ной (или силой всемирного тяготе- ния). Силы тяготения всегда являются силами притяжения и направлены вдоль прямой, проходящей через взаимодей- ствующие тела. Коэффициент пропор- циональности G называется гравита- ционнойпостоянной.

Закон всемирного тяготения спра- ведлив лишь для тел, которые можно считать материальными точками, т.е. для таких тел, размеры которых малы по сравнению с расстоянием между ними. Для вычисления силы взаимо- действия между протяженными (не то- чечными) телами их следует «разбить» на элементарные массы, чтобы их мож- но было считать материальными точка- ми, подсчитать по формуле (22.1) силы притяжения между всеми попарно взя-

тыми элементами, а затем геометриче- ски их сложить (проинтегрировать), что является довольно сложной мате- матической задачей.

Впервые экспериментальное доказа- тельство закона всемирного тяготения для земных тел, а также числовое опре- деление гравитационной постоянной G проведено английским физиком Г. Ка- вендишем (1731-1810).

Принципиальная схема опыта Ка- вендиша, применившего крутильные весы, представлена на рис. 39. Легкое коромысло А с двумя одинаковыми шариками массой т = 729 г подвешено на упругой нити В. На коромысле С укреплены на той же высоте массивные шары массой М = 158 кг. Поворачивая коромысло С вокруг вертикальной оси, можно изменять расстояние между ша- рами с массами т и М. Под действием пары сил, приложенных к шарикам т со стороны шаров М, коромысло А по- ворачивается в горизонтальной плоско- сти, закручивая нить В до тех пор, пока момент сил упругости не уравновесит момент сил тяготения. Зная упругие свойства нити, по измеренному углу поворота можно найти возникающие силы притяжения, а так как массы ша- ров известны, то и вычислить значе- ние G.

Значение G— фундаментальная фи- зическая постоянная, принимаемая равной 6,6720 • 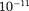Н • 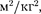т.е. два точечных тела массой по 1 кг каждое, находящиеся на расстоянии 1 м друг от друга, притягиваются с силой

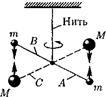Рис. 39

• 10 H. Очень малая величина что сила гравитационно-

го взаимодействия может быть значи- тельной только в случае больших масс.

§ 23. Сила тяжести и вес.

Невесомость

Вблизи поверхности Земли все тела падают с одинаковым ускорением, ко- торое получило название ускорения свободного падения д. Таким образом, в системе отсчета, связанной с Землей, на всякое тело массой т действует сила

называемая силой тяжести.

Согласно фундаментальному физи- ческому закону — обобщенному зако- ну Галилея, все тела в одном и том же поле тяготения падают с одинаковым ускорением. Следовательно, в данном месте Земли ускорение свободного па- дения одинаково для всех тел. Оно из- меняется вблизи Земли с в пределах от 9,780 м/с2на эк- ваторе до 9,832 м/с2 на полюсах. Это обусловлено суточным вращением Зем- ли вокруг своей оси, с одной стороны, и сплюснутостью Земли — с другой (эк- ваториальный и полярный радиусы Земли равны соответственно 6378 и 6357 км). Так как различие значений д невелико, то ускорение свободного па- дения, которое используется при реше- нии практических задач, принимается равным 9,81 м/с2.

Если пренебречь суточным враще- нием Земли вокруг своей оси, то сила тяжести и сила гравитационного тяго- тения равны между собой:

где М — масса Земли; R —расстояние между телом и центром Земли.

Эта формула дана для случая, когда тело находится на поверхности Земли.

Если тело расположено на высоте h от поверхности Земли, Ro — радиус Земли, тогда

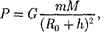т. е. сила тяжести с удалением от поверх- ности Земли уменьшается.

Весом тела называют силу, с кото- рой тело действует на опору (или под- вес) вследствие гравитационного при- тяжения к Земле. Вес тела проявляет- ся только в том случае, если тело дви- жется с ускорением, отличным от д, т. е. когда на тело кроме силы тяжести дей- ствуют другие силы. Состояние тела, при котором оно движется только под действием силы тяжести, называется состоянием невесомости.

Таким образом, сила тяжести дей- ствует всегда, а вес проявляется толь- ко в том случае, когда натело кромесилы тяжести действуют еще другие силы, вследствие чего тело движется с уско- рением отличным от Если тело дви- жется в ноле тяготения Земли с уско- рением а д, то к этому телу приложе- на дополнительная сила N, удовлетво- ряющая условию

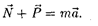
Тогда вес тела

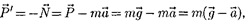
т.е. если тело покоится или движется прямолинейно и равномерно, то =

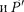— тд. Если тело свободно движет- ся в поле тяготения по любой траекто- рии и в любом направлении, то а = g и р' = т. е. тело будет невесомым. На- пример, невесомыми являются тела, на-

ходящиеся в космических кораблях, свободно движущихся в космосе.

§ 24. Поле тяготения и его напряженность

Закон тяготения Ньютона (22.1) оп- ределяет зависимость силы тяготения от масс взаимодействующих тел и рас- стояния между ними, но не показыва- ет, как осуществляется это взаимодей- ствие. Тяготение принадлежит к особой группе взаимодействий. Силы тяготе- ния не зависят от того, в какой среде находятся взаимодействующие тела. Тяготение существует и в вакууме.

Гравитационное взаимодействие между телами осуществляется с помо- щьюполятяготения,илигравитаци- онного поля. Это поле порождается те- лами и является формой существова- ния материи. Основное свойство поля тяготения заключается в том, что на всякое тело массой т, внесенное в это поле, действует сила тяготения, т.е.

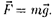(24.1)

Вектор д не зависит от т называ- ется напряженностью поля тяготения. Напряженность поля тяготенияоп- ределяется силой, действующей со сто- роны поля на материальную точку еди- ничной массы, и совпадает по направ- лению с действующей силой. Напря- женность есть силовая характеристи- ка поля тяготения.

Поле тяготения называется одно- родным, если его напряженность во всех точках одинакова, и централь- ным, во всех точках тюля векторы напряженности направлены вдоль пря- мых, которые пересекаются в одной точке неподвижной по отношению к какой-либо инерциалыюй системе отсчета (рис. 40).

Рис. 40

Для графического изображения си- лового поля используются силовые ли- нии (линии напряженности). Силовые линии выбираются так, что вектор на- пряженности поля направлен по каса- тельнойк силовой линии.

§ 25. Работа в поле тяготения.

Потенциал поля тяготения

Определим работу, совершаемую силами поля тяготения при перемеще- нии в нем материальной точки мас- сой т. Вычислим, например, какую надо совершить работу для удаления тела массой m от Земли. Нарасстоянии R (рис. 41) на данное тело действует сила

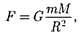где М— масса Земли.

При перемещении этого тела на рас- стояние совершается работа

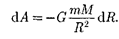(25.1)

Знак «—» появляется потому, что сила и перемещение в данном случае противоположны по направлению (см. рис. 41).

Рис.41

Если тело перемещать с расстояния 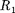до то работа

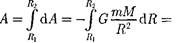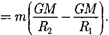(25.2)

Из формулы (25.2) вытекает, что работа в поле тяготения не зависит от траектории перемещения, а определя- ется лишь начальным и конечным по- ложениями тела, т.е. силы тяготения действительно консервативны, а поле тяготения является потенциальным (см. § 12).

Согласно формуле (12.2), работа, совершаемая консервативными силами, равна изменению потенциальной энер- гии системы, взятому со знаком « —», т.е.

Из формулы (25.2) получим

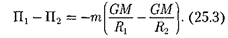Так как в формулы входит только разность потенциальных энергий в двух состояниях, то для удобства принимают потенциальную энергию при равной нулю Тогда (25.3)

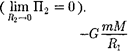запишется в виде П1 = . Так

как первая точка была выбрана произ- вольно, то

Величина

тенциалом. Потенциал поля тяготе- ния ф — скалярная величина, опреде- ляемая потенциальной энергией тела единичной массы в данной точке поля или работой по перемещению единич- ной массы из данной точки поля в бес- конечность. Таким образом, потенциал поля тяготения, создаваемого телом массой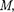

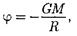(25.4)

где R — расстояние от этого тела до рас- сматриваемой точки.

Из формулы (25.4) вытекает, что гео- метрическое место точек с одинаковым потенциалом образует сферическую по- верхность (R = const). Поверхности, для которых потенциал постоянен, на- зываются эквипотенциальными.

Рассмотрим взаимосвязь между по- тенциалом 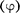поля тяготения PI его напряженностью (д). Из выражений (25.1) и (25.4) следует, что элементар- ная работа совершаемая силами поля при малом перемещении тела мас- сой т,

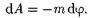
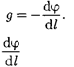С другой стороны, элементарное перемещение). Учитывая (24. 1),

Величина характеризует изме- нение потенциала на единицу длины внаправлении перемещения в поле тяго- тения. Можно показать, что

является энергетической характерис- тикой поля тяготения и называется по-

(25.5)

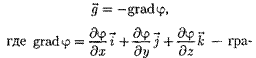
диент скаляра [см. (12.5)]. Знак «—»

в формуле (25.5) показывает, что век- тор напряженности д направлен в сто- рону убывания потенциала.

В качестве частного примера, исхо- дя из представлений теории тяготения, рассмотрим потенциальную энергию тела, находящегося на высоте h относи- тельно Земли:

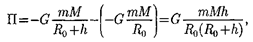где Ro — радиус Земли.

Так как

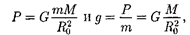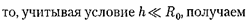
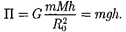Таким образом, мы вывели форму- лу, совпадающую с (12.7), которая по- стулировалась раньше.

§ 26. Космические скорости

Для запуска ракет в космическое пространство надо в зависимости от поставленных целей сообщать им опре- деленные начальные скорости, называ- емые космическими.

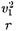
Первой космической (или круго- вой) скоростьюназывают такую ми- нимальную скорость, которую надо со- общить телу, чтобы оно могло двигать- ся вокруг Земли по круговой орбите, т.е. превратиться в искусственный спутник Земли. На спутник, движу- щийся по круговой орбите радиусом г, действует сила тяготения Земли, сооб- щающая ему нормальное ускорение —. По второму закону Ньютона,

Если спутник движется вблизи по- верхности Земли, то 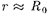(радиус Земли) и д— [см. (25.6)], поэтому

у поверхности Земли

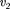Первой космической скорости недо- статочно для того чтобы тело могло выйти из сферы земного притяжения. Необходимая для этого скорость назы- вается второй космической. Второй космической (или параболической) скоростью называют ту наимень- шую скорость, которую надо сообщить телу, чтобы оно могло преодолеть при- тяжение Земли и превратиться в спут- ник Солнца, т. е. чтобы его орбита в поле тяготения Земли стала параболической.

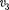Для того чтобы тело (при отсутствии сопротивления среды) могло преодо- леть земное притяжение и уйти в кос- мическое пространство, необходимо, чтобы его кинетическая энергия была равна работе, совершаемой против сил тяготения:

Третьей космической скоростью называют скорость, которую необходи- мо сообщить телу на Земле, чтобы оно покинуло пределы Солнечной системы, преодолев притяжение Солнца. Третья космическая скорость = 16,7 км/с. Сообщение телам таких больших на- чальных скоростей является сложной технической задачей. Ее первое теоре- тическое осмысление начато К. Э. Ци-

51

олковским, им была выведена уже рас- смотренная нами формула (10.3), по- зволяющая рассчитывать скорость ра- кет.

Впервые космические скорости бы- ли достигнуты в СССР: первая — при запуске первого искусственного спут- ника Земли в 1957 г., вторая — при за- пуске ракеты в 1959 г. После историче- ского полета Ю.А.Гагарина в 1961 г. начинается бурное развитие космонав- тики.

§ 27. Неинерциальные системы отсчета. Силы инерции

Как уже отмечалось (см. § 5, 6), за- коны Ньютона выполняются только в инерциальных системах отсчета. Сис- темы отсчета, движущиеся относи- тельно инерциальной системы с уско- рением, называются неинерциалъны- ми. В неинерциальных системах зако- ны Ньютона, вообще говоря, уже не- справедливы. Однако законы динами- ки можно применять и для них, если кроме сил, обусловленных воздействи- ем тел друг на друга, ввести в рассмот- рение силы особого рода — так называ- емые силы инерции.

Если учесть силы инерции, то вто- рой закон Ньютона будет справедлив для любой системы отсчета: произведе- ние массы тела на ускорение в рассмат- риваемой системе отсчета равно сумме всех сил, действующих на данное тело (включая и силы инерции). Силы инер- ции при этом должны быть такими, чтобы вместе с силами F, обусловлен- ными воздействием тел друг на друга, они сообщали телу ускорение 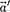каким оно обладает в неинерциальных систе- мах отсчета, т. е.

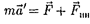(27.1)

Так как F = та (а —ускорение тела в

инерциальной системе отсчета), то

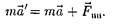
Силы инерции обусловлены уско- ренным движением системы отсчета относительно измеряемой системы, по- этому в общем случае нужно учитывать следующие случаи проявления этих сил: 1) силы инерции при ускоренном поступательном движении системы от- счета; 2) силы инерции, действующие на тело, покоящееся во вращающейся системе отсчета; 3) силы инерции, дей- ствующие на тело, движущееся во вра- щающейся системе отсчета.

Рассмотрим эти случаи.

1. Силы инерции при ускоренном посту- пательном движении системы отсчета.Пусть на тележке к штативу на нити подве- шен шарик массой т (рис. 42). Пока тележ- ка покоится или движется равномерно и прямолинейно, нить, удерживающая шарик, занимает вертикальное положение и сила тяжести Р уравновешивается силой реакции нити

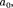
Если тележку привести в поступатель- ное движение с ускорением то нить нач- нет отклоняться от вертикали назад до та- кого угла а, пока результирующая сила =

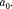
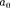
— Р + не обеспечит ускорение шарика, равное Таким образом, результирующая сила направлена в сторону ускорения те- лежки для установившегося движения шарика (шарик теперь движется вместе с те- лежкой с ускорением 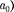равна F= =

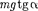— откуда

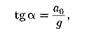т. е. угол отклонения нити от вертикали тем больше, чем больше ускорение тележки.

Относительно системы отсчета, связан- ной с ускоренно движущейся тележкой, шарик покоится, что возможно, если сила F уравновешивается равной и противополож- но направленной ей силой которая яв- ляется не чем иным, как силой инерции, так

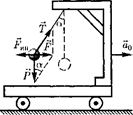Рис. 42

как на шарик никакие другие силы не дей- ствуют. Таким образом,

окружности радиусом 7?. (расстояние от цен- тра вращающегося шарика до оси враще- ния). Следовательно, на пего действует сила, равная F= направленная пер- пендикулярно оси вращения диска. Она яв- ляется равнодействующей силы тяжести Р и силы натяжения нити 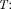F Р + 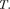Ког- да движение шарика установится, то

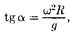
откуда

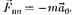(27.2)

Проявление сил инерции при поступа- тельном движении наблюдается в повсе- дневных явлениях. Например, когда поезд набирает скорость, то пассажир, сидящий по ходу поезда, под действием силы инерции прижимается к спинке сиденья. Наоборот, при торможении поезда сила инерции на- правлена в противоположную сторону и пассажир удаляется от спинки сиденья. Осо- бенно эти силы заметны при внезапном тор- можении поезда. Силы инерции проявляют- ся в перегрузках, которые возникают при запуске и торможении космических кораб-

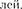
2. Силы инерции, действующие на тело, покоящееся во вращающейся системе от- счета.Пусть диск равномерно вращается с угловой скоростью const) вокруг вер- тикальной оси, проходящей через его центр. На диске, на разных расстояниях от оси вра- щения, установлены маятники (на нитях подвешены шарики массой га). При враще- нии маятников вместе с диском шарики от- клоняются от вертикали на некоторый угол (рис. 43).

В инерциальной системе отсчета, связан- ной, например, с помещением, где установ- лен диск, шарик равномерно вращается по

Рис. 43

т.е. углы отклонения нитей маятников бу- дут тем больше, чем больше расстояние R от центра шарика до оси вращения диска и чем больше угловая скорость вращения

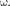
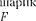Относительно системы связан- ной с вращающимся диском, покоит- ся, что возможно, если сила уравновеши- вается равной и противоположно направ- ленной ей силой которая является не чем иным, как силой инерции, так как па шарик никакие другие силы не действуют. Сила 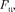называемая центробежной силой инерции, направлена по горизонтали от оси вращения диска и равна

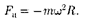(27.3)

Действию центробежных сил инерции подвергаются, например, пассажиры в дви- жущемся транспорте на поворотах, летчи- ки при выполнении фигур высшего пилота- жа; центробежные силы инерции использу- ются во всех центробежных механизмах: насосах, сепараторах и т. д., где они достига- ют огромных значений. При проектирова- нии быстро вращающихся деталей машин (роторов, винтов самолетов и т.д.) принима- ются специальные меры для уравновешива- ния центробежных сил инерции.

Из формулы (27.3) вытекает, что центро- бежная сила инерции, действующая на тела во вращающихся системах отсчета в направ- лении радиуса от оси вращения, зависит от угловой скорости вращения системы отсче- та и радиуса R, но не зависит от скорости тел относительно вращающихся систем отсчета. Следовательно, центробежная сила инерции действует во вращающихся системах отсче- та на все тела, удаленные от оси вращения па конечное расстояние,независимо от того, по-

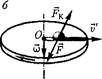
Рис.44

коятся ли они в этой системе (как мы пред- полагали до сих пор) или движутся относи- тельно нее с какой-то скоростью.

3. Силы инерции, действующие на тело, движущееся во вращающейся системе от- счета.Пусть шарик массой га движется с постоянной скоростью v' вдоль радиуса рав- номерно вращающегося диска = const, из = const, v' JL из). ЕСЛИ ДИСК не вращается, то шарик, направленный вдоль радиуса, дви- жется по радиальной прямой и попадает в точку А, если же диск привести во враще- ние в направлении, указанном стрелкой, то шарик катится кривой ОВ (рис. 44, а), причем его скорость v' относительно диска изменяет свое направление. Это возможно лишь тогда, если на шарик действует сила, перпендикулярная скорости

Для того чтобы заставить шарик катить- ся по вращающемуся диску вдоль радиуса, используем жестко укрепленный вдоль ра- диуса диска стержень, на котором шарик движется без трения равномерно и прямо- линейно со скоростью v' (рис. 44, б). При от- клонении шарика действует на него с некоторой силой F. Относительно диска (вращающейся системы отсчета) ша- рик движется равномерно и что можно объяснить тем, что сила F урав-

к шарику си- лой инерции перпендикулярной скоро- сти v'. Эта сила называется

Силой инерции.

Можно показать, что сила Кориолиса1

(27.4)

Вектор перпендикулярен векторам скорости v' тела и угловой скорости враще- ния системы отсчета в соответствии с пра- вилом правого винта.

Г.Кориолис (1792— 1843) — французский физик и инженер.

Рис.45

Сила Кориолиса действует только на тела, движущиеся относительно вращаю- щейся системы отсчета, например относи- тельно Земли. Поэтому действием этих сил объясняется ряд наблюдаемых на Земле яв- лений. Так, если тело движется в Северном полушарии на север (рис. 45), то действу- ющая на него сила Кориолиса, как это сле- дует из выражения (27.4), будет направле- на вправо по отношению к направлению движения, т. е. тело несколько отклонится на восток. Если тело движется на юг, то сила Кориолиса также действует вправо, если смотреть по направлению движения, т.е. тело отклонится на запад. Поэтому в Северном полушарии наблюдается более сильное подмывание правых берегов рек; правые рельсы железнодорожных путей по движению изнашиваются быстрее, чем ле- вые, и т.д. Аналогично можно показать, что в Южном полушарии сила Кориолиса, дей- ствующая на движущиеся тела, будет на- правлена влево по отношению к направле- нию движения.

Благодаря силе Кориолиса падающие на поверхность Земли тела отклоняются к во- стоку (на широте 60° это отклонение долж- но составлять 1 см при падении с высоты 100 м). С силой Кориолиса связано поведе- ние маятника Фуко, явившееся в свое вре- мя одним из доказательств вращения Зем- ли. Если бы этой силы не было, то плоскость колебаний качающегося вблизи поверхнос- ти Земли маятника оставалась бы неизмен- ной (относительно Земли). Действие же сил Кориолиса приводит к вращению плоскости колебаний вокруг вертикального направле- ния.

Раскрывая содержание 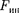в форму- ле (27.1), получим основной закон ди-

намики для неинерциальных систем отсчета:

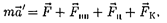
где силы инерции задаются формулами (27.2)-(27.4).

Обратим еще раз внимание на то, что силы инерции вызываются не взаимо- действием тел, а ускоренным движени- ем системы отсчета. Поэтому они не подчиняются третьему закону Ньюто- на, так как если на какое-либо тело дей- ствует сила инерции, то не существует противодействующей силы, приложен- ной к данному телу. Два основных по- ложения механики, согласно которым ускорение всегда вызывается силой, а сила всегда обусловлена взаимодей- ствием между телами, в системах отсче- та, движущихся с ускорением, одновре- менно не выполняются.

Для любого из тел, находящихся в неинерциалыюй системе отсчета, силы инерции являются внешними, следова- тельно, здесь нет замкнутых систем. Это означает, что в неинерциальных систе- мах отсчета не выполняются законы сохранения импульса, энергии и момен- та импульса. Таким образом, силы инер- ции действуют только в неинерциаль- ных системах. В инерциальных систе- мах отсчета таких сил не существует.

Возникает вопрос о «реальности» или

«фиктивности» сил инерции. В ньютонов- ской механике, согласно которой сила есть результат взаимодействия тел, на силы инерции можно смотреть как на «фиктив- ные», «исчезающие» в инерциальных систе- мах отсчета. Однако возможна и другая их интерпретация. Так как взаимодействия тел

осуществляются посредством силовых по- лей, то силы инерции рассматриваются как воздействия, которым подвергаются тела со стороны каких-то реальных силовых полей, и тогда их можно считать «реальными». Независимо от того, рассматриваются ли силы инерции в качестве «фиктивных» или

«реальных», многие явления, о которых упо- миналось в настоящем параграфе, объясня- ются с помощью сил инерции.

Силы инерции, действующие на тела в иеинерциалыюй системе отсчета, пропорци- ональны их массам и при прочих равных условиях сообщают этим телам одинаковые ускорения. Поэтому в «поле сил инерции» эти тела движутся совершенно одинаково, если только одинаковы начальные условия. Тем же свойством обладают тела, находящи- еся под действием сил поля тяготения.

При некоторых условиях силы инерции и силы тяготения невозможно различить. Например, движение тел в равноускорен- ном лифте происходит точно так же, как и в неподвижном лифте, висящем в однород- ном поле тяжести. Никакой эксперимент, выполненный внутри лифта, не может от- делить однородное поле тяготения от одно- родного поля сил инерции.

Аналогия между силами тяготения и силами инерции лежит в основе прин- ципа эквивалентности гравитационных сил и сил инерции (принципа эквива- лентности Эйнштейна): все физичес- кие явления в поле тяготения происхо- дят совершенно так же, как и в соответ- ствующем поле сил инерции, если на- пряженности обоих полей в соответ- ствующих точках пространства совпа- дают, а прочие начальные условия для рассматриваемых тел одинаковы. Этот принцип является основой общей тео- рии относительности.

Контрольные вопросы

Как определяется гравитационная постоянная и каков ее физический смысл?

На какой высоте над планетой ускорение свободного падения вдвое меньше, чем на ее поверхности?

Что такое вес тела?

В чем отличие веса тела от силы тяжести?

Как объяснить возникновение невесомости при свободном падении? Что такое напряженность поля тяготения?

Какое поле тяготения называется однородным? центральным?

Какие величины вводятся для характеристики поля тяготения и какова связь между ними?

Покажите, что силы тяготения консервативны.

Чему равно максимальное значение потенциальной энергии системы из двух тел, нахо- дящихся в поле тяготения?

Какие траектории движения имеют спутники, получившие первую и вторую космиче- ские скорости?

Как вычисляются первая и вторая космические скорости? Когда и почему необходимо рассматривать силы инерции?

Что такое силы инерции? Чем они отличаются от сил, действующих в инерциальных системах отсчета?

Как направлены центробежная сила инерции и сила Кориолиса? Когда они проявля- ются?

В Северном полушарии производится выстрел вдоль па север. Как скажется на движении снаряда суточное вращение Земли?

Сформулируйте и поясните принцип эквивалентности Эйнштейна.

ЗАДАЧИ

5.1. Два одинаковых однородных шара из одинакового материала, соприкасаясь друг с другом, притягиваются. Определите, как изменится сила притяжения, если массу шаров увеличить в 4 раза. [Возрастет в 6,35 раза]

5.2. Плотность вещества некоторой шарообразной планеты составляет 3 г/см3. Каким должен быть период обращения планеты вокруг собственной оси, чтобы на экваторе тела были невесомыми?

5.3. Определите, в какой точке (считая от Земли) на прямой, соединяющей центры Зем-

ли и Луны, напряженность поля тяготения равна нулю. Расстояние между центрами Земли и Луны равно R, масса Земли в 31 раз больше массы Луны.

5.4. Два одинаковых однородных шара из одинакового материала соприкасаются друг с другом. Определите, как изменится потенциальная энергия их гравитационного взаимо- действия, если массу шаров увеличить в четыре раза. [Возрастет в 14,6 раза]

5.5. Два спутника одинаковой массы движутся вокруг Земли по круговым орбитам ра-

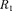
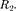
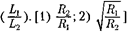диусами и Определите: 1) отношение полных энергий 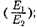2) отноше- ние их моментов импульса

5.6. Вагон катится вдоль горизонтального участка дороги. Сила трения составляет 20 % от веса вагона. К потолку вагона на нити подвешен шарик массой 10 г. Определите:

1) силу, действующую на нить; 2) угол отклонения нити от вертикали. [1) 0,1 Н; 2)11°35']

5.7. Тело массой 1,5 кг, падая свободно в 5 с, попадает на Землю в точку с географической широтой = 45°. Учитывая вращение Земли, нарисуйте и определите все силы, действующие на тело в момент его падения на Землю. [1) 14,7 Н; 2) 35,7 Н;

3) 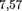мН] 56

Глава 6

ЭЛЕМЕНТЫ МЕХАНИКИ ЖИДКОСТЕЙ

§ 28. Давление жидкости и газа

Молекулы газа, совершая беспоря- дочное, хаотическое движение, не свя- заны или весьма слабо связаны силами взаимодействия, поэтому они движут- ся свободно и в р