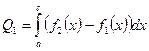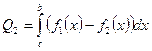Вычисление площадей плоских фигур

Вычисление площадей плоских фигур

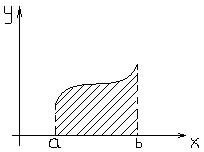
Если функция 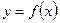, определена и интегрируема на отрезке 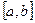, причем 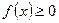на этом отрезке, то площадь криволинейной трапеции определяется определенным интегралом. 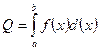. Если функция отрицательна на отрезке

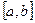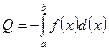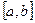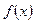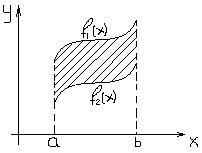
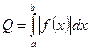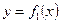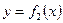, то . Если функция принимает как положительные, так и отрицательные значения, то для определения площади криволинейной трапеции в обычном смысле, необходимо разбить отрезок , на части, соответствующие участкам знакопостоянства функции . Площадь криволинейной трапеции будет выражена: . Если требуется вычислить площадь области ограниченной двумя кривыми и на отрезке 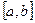. Причем 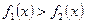, то достаточно представить искомую площадь в виде разности площадей двух криволинейных трапеций.

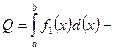
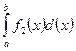
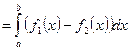
В случае более сложных областей, искомую площадь разбивают на части и каждую часть рассчитывают по отдельности.

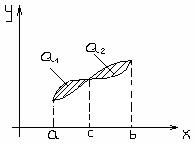
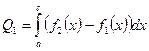
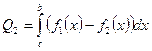
Вычисление площади криволинейной трапеции заданной в параметрической форме

Пусть функция y=f(x) на отрезке [a,b] задана параметрически

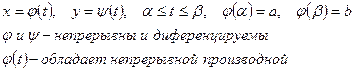
Следовательно, площадь криволинейной трапеции может быть вычислена по формуле

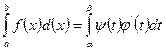
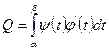
Пример. Вычислить площадь эллипса.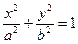

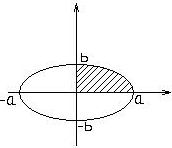Эллипс- фигура симметричная по всем осям, для вычисления площади эллипса достаточно вычислить площадь заштрихованной части. Используя тригонометрическую параметризацию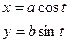 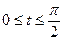, получим

.

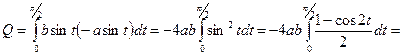
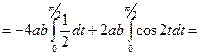
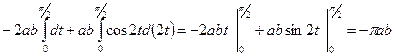
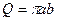Площадь криволинейного сектора

В полярной системе координат положение точки на плоскости определяется парой чисел: 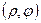. Число 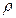определяет расстояние от точки М до полюса. 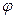- угол образованный отрезком ОМ и полярной осью.

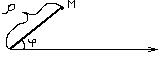
Если полюс совпадает с началом декартовой системы координат, а ось х совпадает с полярной осью, то между декартовой и полярной системами координат, существует связь.

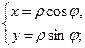
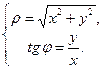
При нахождении 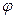нужно учитывать, в какой четверти находится точка, и брать соответствующее значение.

В полярной системе координат уравнение кривой может быть записано в ви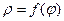де

где 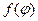- непрерывная функция, .

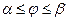Находясь в полярной системе координат, получим выражение для площади сектора ОАВ ограниченного кривой 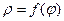и радиус векторами 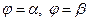. Разобьём данную область радиус – векторами 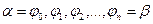на n – частей. Обозначим через 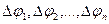- углы между радиус векторами.

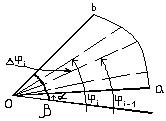
Обозначим через 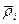-некоторый радиус-вектор, соответствующий углу , .

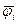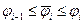Рассмотрим круговой сектор с радиусом 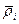и центральным углом 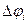. Площадь кругового сектора равна: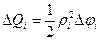

Сумма 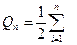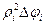= 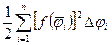даёт площадь ступенчатого сектора. Так как эта сумма является интегральной суммой для функции 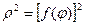на отрезке 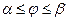, то её предел есть неопределённый интеграл 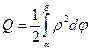. Выписанный интеграл считают площадью криволинейного сектора ОАВ.

Длина дуги кривой

Объём тела вращения

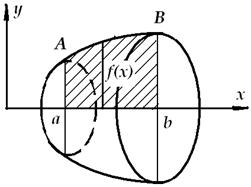
Вычислим объем тела, получаемый от вращения криволинейной трапеции вокруг оси ох.

В каждом сечении тела плоскостью перпендикулярной оси х получим круг, площадью которого 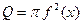и объем тела вращения

.

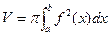Несобственные интегралы.

Рассматривая понятие определенного интеграла, существенно выделяли 2 обстоятельства:

1) Отрезок, по которому ведется интегрирование, должен быть конечным.

2) Функция 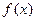, стоящая под знаком интеграла 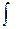, должна быть ограничена на отрезке .

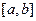Понятие предела позволяет обобщить понятие определенного интеграла на случай бесконечного промежутка интегрирования и на случай неограниченной функции. Соответствующие интегралы называются несобственными интегралами первого и второго рода.

Несобственный интеграл первого рода - интеграл по бесконечному промежутку.

Несобственный интеграл второго рода - интеграл от неограниченной функции.

Вычисление площадей плоских фигур

Если функция 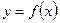, определена и интегрируема на отрезке 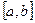, причем 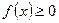на этом отрезке, то площадь криволинейной трапеции определяется определенным интегралом. 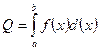. Если функция 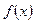отрицательна на отрезке

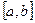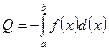, то . Если функция принимает как положительные, так и отрицательные значения, то для определения площади криволинейной трапеции в обычном смысле, необходимо разбить отрезок 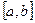, на части, соответствующие участкам знакопостоянства функции 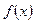. Площадь криволинейной трапеции будет выражена: 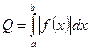. Если требуется вычислить площадь области ограниченной двумя кривым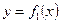и и 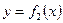на отрезке 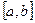. Причем 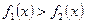, то достаточно представить искомую площадь в виде разности площадей двух криволинейных трапеций.

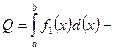
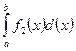
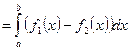
В случае более сложных областей, искомую площадь разбивают на части и каждую часть рассчитывают по отдельности.